Les postulats de la mÃĐcanique quantique
version disponible en : en it ru zh es ja de nl pt
crée le : 20241110- mis à jour le : 20241110- généré le: 20241110_231431
Cet article prÃĐsente en dÃĐtail les postulats_de_la_mÃĐcanique_quantique
à partir de considÃĐrations mathÃĐmatiques et gÃĐomÃĐtriques simples et des analogies prises dans la vie quotidienne.
En physique on ÃĐlabore des concepts reliÃĐs à des objets mathÃĐmatiques pour ÃĐtablir
des thÃĐories qui permettent de reprÃĐsenter le monde physique à travers ses lois de fonctionnement.
La mÃĐcanique classique ou thÃĐorie de Newton est la thÃĐorie qui permet de reprÃĐsenter le
fonctionnement de la matiÃĻre aux ÃĐchelles sensibles à la perception humaine
que l'on nomme macroscopiques.
Aux ÃĐchelles cosmologiques cette thÃĐorie est gÃĐnÃĐralisÃĐe à travers les thÃĐories relativistes d'Einstein.
La relativitÃĐ gÃĐnÃĐrale est la thÃĐorie qui traite le plus complÃĻtement la force de gravitation.
La mÃĐcanique quantique est la thÃĐorie qui permet de reprÃĐsenter le fonctionnement de la matiÃĻre au niveau microscopique bien que la limite entre le microscopique et le macroscopique ne soit pas clairement dÃĐfinie en terme d'ÃĐchelle de grandeur si bien que l'on peut avoir des comportements quantiques aux ÃĐchelles macroscopiques comme dans le laser ou les cables_ÃĐlectriques_supraconducteurs
La thÃĐorie quantique ne traite pas d'une force de la nature en particulier comme la relativitÃĐ gÃĐnÃĐrale,
elle est plus un langage. Le langage des objets quantiques. Ainsi on pourra appliquer ce langage
à diverses forces ou systÃĻmes, on rÃĐalise ainsi leur quantification.
Le jeu des concepts quantiques s'articule autour de six postulats de base qui dÃĐfinissent complÃĻtement la thÃĐorie quantique.
Nous allons prÃĐsenter ces six postulats et essayer d'en dÃĐgager leur signification
de maniÃĻre simple.
L'expression du premier postulat tel qu'il est dÃĐfini dans le livre "MÃĐcanique Quantique Tome 1" de Cohen-Tanoudji est :
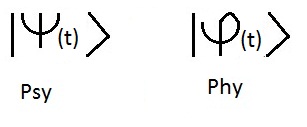
" A un instant t fixÃĐ, l'ÃĐtat d'un systÃĻme physique est dÃĐfini par la donnÃĐe
d'un ket ou fonction d'onde ou vecteur d'ÃĐtat notÃĐ |psy(t)> appartenant à l'espace des ÃĐtats".
La lettre grecque Psy est utilisÃĐe pour dÃĐsigner la fonction d'onde, on utilise
aussi indiffÃĐremment la lettre Phy.

Le premier concept de la mÃĐcanique porte sur la reprÃĐsentation de l'ÃĐtat du systÃĻme physique.
C'est une façon naturelle de dÃĐfinir l'objet de l'ÃĐtude. Ici on dit simplement que le systÃĻme existe
et que l'on peut reprÃĐsenter son ÃĐtat par une fonction qui dÃĐpend du temps
ceci parce que l'ÃĐtat du systÃĻme n'est à priori pas statique mais dynamique.
En mÃĐcanique classique le systÃĻme physique est reprÃĐsentÃĐ par le "point matÃĐriel".
Un systÃĻme complexe sera reprÃĐsentÃĐ par un ensemble de points matÃĐriels reliÃĐs
entre eux pour former un objet solide ou non (liaisons rigides ou non, par exemple: cristal ou gaz).
Le premier postulat dit simplement que l'ÃĐtat du systÃĻme à un instant donnÃĐ est unique
et appartient à un ensemble d'ÃĐtats possibles regroupÃĐs dans un ensemble
mathÃĐmatique nommÃĐ "espace des ÃĐtats".
On parle d'espace et non simplement d'ensemble car l'ÃĐtat quantique est un vecteur
qui est un objet mathÃĐmatique qui reprÃĐsente une direction dans un espace.
Nous connaissons tous l'espace à trois dimensions (longueur, largeur, hauteur ou profondeur suivant l'orientation des deux premiÃĻres dimensions)
Il s'agit de l'espace physique dans lequel nous vivons.
L'espace des ÃĐtats dans lequel "vivent" les systÃĻmes quantiques n'est pas un espace physique, c'est un espace abstrait (espace de Hilbert)
et sa dimension est infinie pour reprÃĐsenter l'infinitÃĐ des ÃĐtats possibles qui existent mÊme pour des systÃĻmes physiques simples.
Nous allons faire une analogie avec un exemple de la vie de tous les jours
pour comprendre comment est modÃĐlisÃĐ un systÃĻme quantique.
Imaginons une personne tranquille dans son appartement et qui soudainement
rÃĐalise qu'elle doit sortir pour aller acheter du pain.
Elle se prÃĐpare à partir et dans son esprit elle hÃĐsite encore de l'endroit oÃđ elle va se rendre pour aller acheter du pain.
Elle a le choix entre une boulangerie plus haut dans sa rue ou une pÃĒtisserie qui fait aussi
du pain et qui se trouve elle, plus bas dans sa rue.
En descendant l'escalier pour sortir on peut dire qu'il y a deux ÃĐtats possibles dans son esprit qui correspondent aux deux options pour acheter du pain. On peut noter ces options à la maniÃĻre quantique:
ÃĐtat 1: |boulanger>
ÃĐtat 2: |pÃĒtissier>
L'ÃĐtat d'esprit de la personne est une combinaison de ces deux possibilitÃĐs:
| Etat> = |boulanger> + |pÃĒtissier>
Les deux ÃĐtats sont complÃĻtement incompatibles: soit elle achÃĻte le pain chez le boulanger, soit chez le pÃĒtisser. Ces deux possibilitÃĐs n'ont absolument rien en commun, elles ne partagent rien. GÃĐomÃĐtriquement on dira qu'elles sont orthogonales (perpendiculaires) et la reprÃĐsentation gÃĐomÃĐtrique dans l'espace (des ÃĐtats donc) sera:
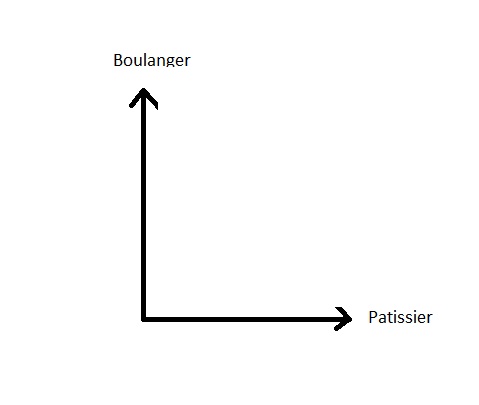
On a donc deux directions bien distinctes qui n'ont rien en commun.
Si la flÃĻche (vecteur) boulanger ÃĐtait penchÃĐe vers la flÃĻche (vecteur) pÃĒtissier
alors cela voudrait dire que le fait d'aller acheter chez
le boulanger est un peu liÃĐ avec le fait d'aller acheter
chez le pÃĒtissier ce qui n'est pas le cas, ce sont deux
options incompatibles: orthogonales, c'est à dire à angle droit: elles ne partagent rien en terme de direction.
Par contre l'ÃĐtat du systÃĻme, c'est à dire l'ÃĐtat d'esprit
de la personne est une combinaison dite linÃĐaire des deux ÃĐtats.
On dit que l'on a un mÃĐlange d'ÃĐtat. L'ÃĐtat rÃĐel mÃĐlangÃĐ ne
correspond pas à quelque chose d'observable: on ne sait
pas ou le pain est achetÃĐ.
Cette combinaison linÃĐaire des deux possibilitÃĐs correspond
à la somme des deux vecteurs qui reprÃĐsentent les ÃĐtats observables.
La somme de deux vecteurs se rÃĐalise de la façon suivante : on fait
partir le deuxiÃĻme vecteur de la fin du premier vecteur et le vecteur
somme rÃĐsultant part du dÃĐbut du premier et se termine vers la fin
du second.
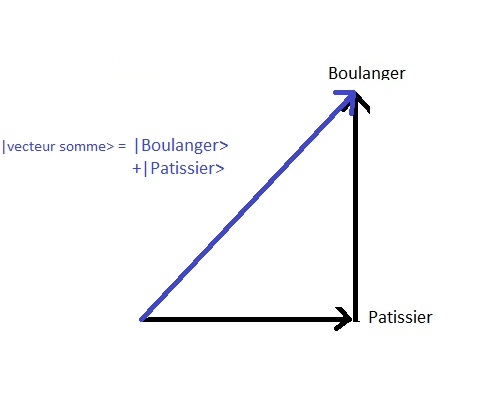
On a dit que l'espace des ÃĐtats ÃĐtait un espace vectoriel, c'est à dire un espace de directions, cela implique que dans la reprÃĐsentation gÃĐomÃĐtrique on peut dÃĐplacer les vecteurs sans en changer la nature, ils restent les mÊmes vecteurs: ils indiquent la mÊme direction. Aussi pour simplifier la reprÃĐsentation on fait partir tous les vecteurs du mÊme point pour indiquer que seules les directions existent dans cet espace. C'est ce qu'on appelle un espace vectoriel par opposition à un espace de points qui est appelÃĐ en mathÃĐmatique un espace affine. ( L'ÃĐcran sur lequel vous lisez ce texte est un exemple d'espace affine ou les pixels reprÃĐsentent les points de cet espace.)
La reprÃĐsentation gÃĐomÃĐtrique, elle, se fait ÃĐvidemment dans un espace de points car un espace vectoriel
est une abstraction pure et ne peut Être reprÃĐsentÃĐ dans l'espace que nous percevons qu'avec des points (positions) diffÃĐrents.
Mais cela n'existe pas dans l'espace des ÃĐtats oÃđ toutes les reprÃĐsentations d'un vecteur se trouvant à diffÃĐrentes
positions dans l'espace de reprÃĐsentation correspondent à un vecteur unique dans l'espace vectoriel.
Ainsi on peut reprÃĐsenter l'ÃĐtat de la maniÃĻre suivante :
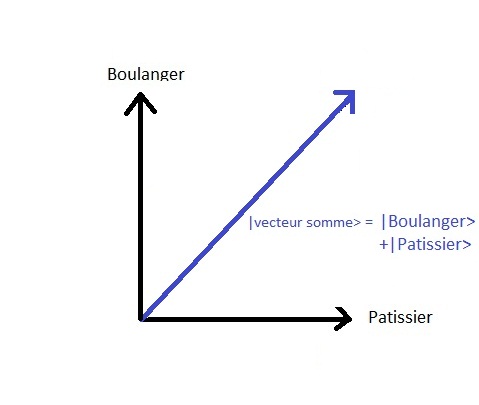
Ici la dimension de l'espace des ÃĐtats est deux. Si il y avait une troisiÃĻme option
avec un autre boulanger dans une rue adjacente | boulanger2 > alors l'espace des ÃĐtats serait de dimension trois, etc.
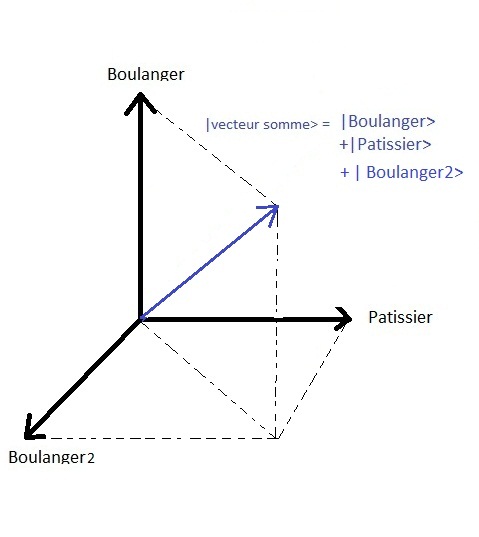
En physique on peut modÃĐliser des systÃĻmes à deux ÃĐtats de la mÊme maniÃĻre.
C'est le cas de la molÃĐcule d'hydrogÃĻne ionisÃĐe. La molÃĐcule d'hydrogÃĻne
est composÃĐe de deux noyaux d'hydrogÃĻne c'est à dire deux protons
et le fait qu'elle soit ionisÃĐe signifie qu'on lui a arrachÃĐ un ÃĐlectron
sur les deux qu'elle possÃĻde naturellement. On prend cet exemple
parce qu'il est simple : "Ã un seul ÃĐlectron".
Les deux ÃĐtats de positions possibles pour l'ÃĐlectron sont :
La reprÃĐsentation gÃĐomÃĐtrique est:
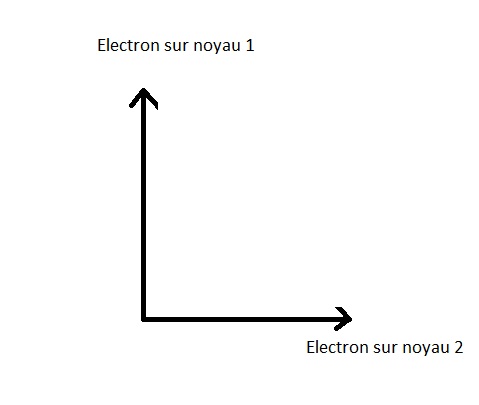
Il est clair que l'ÃĐlectron ne peut se trouver (ou plutÃīt se faire trouver c'est à dire : Être observÃĐ) en mÊme temps sur le noyau 1 et le noyau 2, ces ÃĐtats sont orthogonaux.
Dans l'expression du postulat on utilise des synonymes pour dÃĐsigner le vecteur d'ÃĐtat que l'on appelle indiffÃĐremment
vecteur d'ÃĐtat, fonction d'onde ou ket. Ces diffÃĐrents noms correspondent à diffÃĐrents aspects mathÃĐmatiques du vecteur d'ÃĐtat.
On verra l'aspect fonction d'onde dans l'explication du deuxiÃĻme postulat et l'aspect "ket" dans le troisiÃĻme.
En rÃĐsumÃĐ, l'ÃĐtat quantique est reprÃĐsentÃĐ par la donnÃĐe d'un vecteur (direction) dans un espace vectoriel (de directions),
ce vecteur est nommÃĐ "vecteur d'ÃĐtat".
En mÃĐcanique classique, l'ÃĐtat est reprÃĐsentÃĐ par le "point matÃĐriel" qui est dÃĐfini par ses propriÃĐtÃĐs physiques que sont la position et la vitesse.
On peut remarquer, et c'est important, qu'en mÃĐcanique quantique l'ÃĐtat du systÃĻme est totalement indÃĐpendant
des propriÃĐtÃĐs physiques du systÃĻme. L'ÃĐtat est dÃĐfini de maniÃĻre abstraite et on pourrait dire "non physique".
Ceci sera dÃĐtaillÃĐ dans la prÃĐsentation des postulats suivants à travers la notion de "base de reprÃĐsentation du vecteur d'ÃĐtat".
Mais on peut remarquer que le premier postulat ne fait dÃĐpendre le vecteur d'ÃĐtat que du temps et non de la position
qui est l'espace. Cela signifie que la fonction d'onde est non-locale.
Evidemment la relativitÃĐ nous enseigne que le temps et l'espace forme un continuum et donc si une formulation de
la mÃĐcanique quantique prend en compte au moins la relativitÃĐ restreinte, le vecteur d'ÃĐtat ne dÃĐpend pas non plus
du temps. Cette thÃĐorie est l'ÃĐlectrodynamique quantique ou thÃĐorie quantique du champ ÃĐlectromagnÃĐtique.
La relativitÃĐ restreinte ÃĐtant trÃĻs liÃĐe à l'ÃĐlectromagnÃĐtisme par le fait qu'Einstein a produit cette thÃĐorie
pour lever les paradoxes que la thÃĐorie ÃĐlectromagnÃĐtique de Maxwell soulevait.
Les concepts quantiques n'ont pas ÃĐtÃĐ conçus par pure imagination. Ils ont plutÃīt ÃĐtÃĐ forgÃĐs au feu des expÃĐrimentations
de microphysique qui ont nÃĐcessitÃĐ ces concepts pour pouvoir Être reprÃĐsentÃĐes correctement.
Bien que totalement abstrait l'ÃĐtat quantique n'en est pas moins rÃĐel pour autant.
C'est d'ailleurs cette rÃĐalitÃĐ de l'ÃĐtat quantique qui reste souvent la chose la plus difficile à admettre mÊme si cela est incontournable.
Le fonctionnement de la matiÃĻre qui est la chose la plus concrÃĻte, est gouvernÃĐ par quelque chose de totalement abstrait.
NÃĐanmoins il est impossible de contourner cette difficultÃĐ tant ce concept quantique est extraordinairement solide.
La situation cognitive est un peu similaire à la dÃĐcouverte des ondes ÃĐlectromagnÃĐtiques. Ces ondes ont ÃĐtÃĐ d'abord thÃĐoriquement
dÃĐcouvertes en combinant les ÃĐquations de Maxwell qui dÃĐcrivent les champs ÃĐlectriques et magnÃĐtiques.
Leur combinaison a fourni une ÃĐquation de propagation d'onde avec une vitesse constante. C'ÃĐtait une notion abstraite
et nouvelle mais les expÃĐriences tentÃĐes ont montrÃĐ qu'effectivement les champs ÃĐlectriques et magnÃĐtiques produisaient des ondes
que l'on pouvait contrÃīler et utiliser, ce qui a donnÃĐ lieu à la communication par radio.
On a vu que cette vitesse ÃĐtait la vitesse mesurÃĐe de la lumiÃĻre.
De la mÊme façon le concept trÃĻs abstrait de fonction d'onde est devenu trÃĻs concret dans les expÃĐriences d'intrication_quantique et a donnÃĐ lieu au domaine technologique de la cryptographie_quantique
"Toute grandeur physique observable 'a' est dÃĐcrite par un opÃĐrateur 'A' agissant dans l'espace des ÃĐtats; cet opÃĐrateur est une observable."
En mÃĐcanique classique on a vu que se sont les propriÃĐtÃĐs du point matÃĐriel, sa vitesse et sa position qui dÃĐtermine son ÃĐtat.
Par exemple la vitesse et la position d'une balle sur un cours de tennis ou bien d'une planÃĻte dans le systÃĻme solaire.
La position et la vitesse d'un objet macroscopique sont dÃĐterminÃĐes à chaque instant et cela dÃĐfinit complÃĻtement l'ÃĐtat du systÃĻme.
L'ÃĐvolution de la balle de tennis dans l'espace dÃĐfinit à chaque instant l'ÃĐtat du jeu, si la balle est en mouvement, "out" ou non
ou bien immobile à terre aprÃĻs avoir pris le filet. Et c'est l'historique de ses ÃĐtats qui dÃĐfinit le match et son rÃĐsultat.
Par contre en mÃĐcanique quantique l'ÃĐtat gÃĐnÃĐral d'un systÃĻme rÃĐduit à une particule comme l'ÃĐlectron de l'exemple prÃĐcÃĐdent
n'est plus associÃĐ Ã une position ou une vitesse particuliÃĻre mais à un mÃĐlange de toutes les positions ou de toutes les vitesses possibles.
De plus on ne peut observer toutes les propriÃĐtÃĐs du systÃĻme en mÊme temps comme en mÃĐcanique classique.
Si le systÃĻme est dans un ÃĐtat de position, c'est qu'il n'est pas dans un ÃĐtat d'ÃĐnergie et vice-versa.
Dans l'exemple du pain on a des ÃĐtats de positions qui sont le boulanger et le pÃĒtissier
qui indiquent l'endroit oÃđ le pain est achetÃĐ mais comme nous allons le voir,
ce ne sont pas des ÃĐtats d'ÃĐnergie.
Tout comme dans l'exemple de la molÃĐcule d'hydrogÃĻne le fait que l'ÃĐlectron soit
localisÃĐ sur le noyau 1 ou sur le noyau 2 reprÃĐsente des ÃĐtats de position mais
ce ne sont pas en soi des ÃĐtats d'ÃĐnergie de la molÃĐcule.
Dans un systÃĻme quantique les diffÃĐrentes propriÃĐtÃĐs partagent le mÊme espace d'ÃĐtats
mais les ÃĐtats correspondant à des propriÃĐtÃĐs diffÃĐrentes se sont pas forcÃĐment
reprÃĐsentÃĐs par les mÊmes directions dans l'espace.
Cela veut dire que si l'espace est à deux dimensions alors il y aura deux ÃĐtats
de position possibles mais aussi deux ÃĐtats d'ÃĐnergie possibles et que les ÃĐtats d'ÃĐnergie
n'ont pas les mÊmes directions que les ÃĐtats de position.
Dans le cas de la molÃĐcule d'hydrogÃĻne (ionisÃĐe) les ÃĐtats d'ÃĐnergie possibles sont:
Dans le cas du pain on peut dire que les ÃĐtats d'ÃĐnergie (ÃĐtat d'esprit possible de la personne) sont:
On pourrait dire que l'ÃĐtat d'ÃĐnergie gÃĐnÃĐral est une oscillation entre les deux ÃĐtats d'ÃĐnergie possibles que l'on pourrait appeler "hÃĐsitation".
Ceci illustre bien l'aspect ondulatoire des ÃĐtats qui ne sont pas statiques mais dynamiques.
Ici encore on peut exprimer mathÃĐmatiquement l'ÃĐtat gÃĐnÃĐral du systÃĻme par la combinaison des ÃĐtats particuliers:
| Etat:hÃĐsitation> = |dÃĐtermination> + |renoncement>
dans la reprÃĐsentation "dynamique ou ÃĐnergÃĐtique" du pain.
| Etat:ÃĐnergie> = |ÃĐtat liÃĐ> + |ÃĐtat non-liÃĐ>
dans la reprÃĐsentation "dynamique ou ÃĐnergÃĐtique" de la molÃĐcule d'hydrogÃĻne.
L'ÃĐtat gÃĐnÃĐral du systÃĻme est complÃĻtement indÃĐpendant des propriÃĐtÃĐs de celui-ci ainsi on peut ÃĐcrire pour le pain:
| Etat> = |dÃĐtermination> + |renoncement> = |boulanger> + |pÃĒtissier>
Pour la molÃĐcule d'hydrogÃĻne en appelant El (ÃĐtat liÃĐ) et Enl (ÃĐtat non-liÃĐ) les ÃĐtats d'ÃĐnergie et P1 et P2 les ÃĐtats de position, on a:
| Etat> = | El > + | Enl > = | P1 > + | P2 >
Le fait que l'ÃĐtat soit indÃĐpendant de ses propriÃĐtÃĐs observables et peut s'exprimer indiffÃĐremment
de celles-ci est une caractÃĐristique fondamentale de la mÃĐcanique quantique.
Les propriÃĐtÃĐs sont reprÃĐsentÃĐes par des opÃĐrateurs mathÃĐmatiques qui en s'appliquant sur l'ÃĐtat quantique
dÃĐterminent les ÃĐtats possibles pour cette propriÃĐtÃĐ.
Un opÃĐrateur en mathÃĐmatiques est ce qui fait ÃĐvoluer une valeur au sens large.
Par exemple pour l'addition l'opÃĐrateur "3+" appliquÃĐ Ã "2" donne "3+2"="5" on a fait passer la valeur de "2" Ã "5" par l'application de l'opÃĐrateur "3+" (ajout de la valeur trois)
En mÃĐcanique quantique l'opÃĐrateur fait ÃĐvoluer l'ÃĐtat. Le postulat dit que l'opÃĐrateur "agit" sur l'espace des ÃĐtats.
Soit P l'opÃĐrateur position et E l'opÃĐrateur Energie (en rÃĐalitÃĐ l'opÃĐrateur ÃĐnergie est notÃĐ H pour hamiltonien qui est la fonction ÃĐnergie totale dÃĐfinie de maniÃĻre gÃĐnÃĐrale en mÃĐcanique par Hamilton par la somme de toutes les ÃĐnergies agissant sur le systÃĻme).
D'aprÃĻs le deuxiÃĻme postulat ces opÃĐrateurs reprÃĐsentent les propriÃĐtÃĐs correspondantes (position et ÃĐnergie) du systÃĻme.
En appliquant (faisant agir) l'opÃĐrateur position sur l'ÃĐtat de la molÃĐcule d'hydrogÃĻne on aura:
P | ÃĐtat > = | P1 >
ou
P | ÃĐtat > = | P2 >.
Appliquer l'opÃĐrateur sur l'ÃĐtat revient à observer la propriÃĐtÃĐ correspondant à l'opÃĐrateur, ici la position.
De la mÊme maniÃĻre avec l'opÃĐrateur ÃĐnergie.
H | ÃĐtat > = | El > ou H | ÃĐtat > = | Enl >.
On s'aperçoit ainsi que lorsqu'on applique un opÃĐrateur à un ÃĐtat on fait ÃĐvoluer cet ÃĐtat vers un ÃĐtat
appartenant à cet opÃĐrateur particulier, on appelle cet ÃĐtat "ÃĐtat propre" de l'opÃĐrateur.
Le rÃĐsultat peut Être n'importe quel ÃĐtat possible pour le systÃĻme et pour l'opÃĐrateur (la propriÃĐtÃĐ mesurÃĐe).
L'ÃĐtat "molÃĐcule liÃĐe" est un ÃĐtat propre de l'opÃĐrateur ÃĐnergie tandis que l'ÃĐtat "ÃĐlectron sur le noyau 1"
est un ÃĐtat propre de l'opÃĐrateur position.
Pour la molÃĐcule d'hydrogÃĻne lorsqu'on se trouve dans l'ÃĐtat liÃĐ, l'ÃĐlectron se trouve dans un ÃĐtat de position indÃĐterminÃĐ entre les deux noyaux d'hydrogÃĻne. On peut dire que l'ÃĐtat propre d'ÃĐnergie est une combinaison linÃĐaire d'ÃĐtats de position ce qui peut se reprÃĐsenter ainsi:
| El > = | P1 > + | P2 >
On peut dire que les deux ÃĐtats de position s'ajoutent pour former un ÃĐtat d'ÃĐnergie: lorsque l'ÃĐlectron
est partagÃĐ par les deux noyaux, la molÃĐcule est liÃĐe, on dit que les deux ÃĐtats de position
interfÃĻrent constructivement pour former l'ÃĐtat d'ÃĐnergie "liÃĐ".
de la mÊme maniÃĻre l'ÃĐtat non-liÃĐ sera reprÃĐsentÃĐ par
| Enl > = | P1 >- | P2 >
on dit que les deux ÃĐtats de position interfÃĻrent destructivement pour crÃĐer l'ÃĐtat d'ÃĐnergie "non-liÃĐ".
Si l'on reprend l'analogie du pain, l'ÃĐtat d'esprit de la personne est une hÃĐsitation entre le fait d'aller acheter du pain chez le boulanger ou le pÃĒtissier mais aussi entre le fait d'aller acheter du pain ou de ne pas en acheter.
On peut dire que la dÃĐtermination d'aller acheter du pain est une interfÃĐrence constructrice de toutes
les possibilitÃĐs pour aller acheter du pain tandis que le renoncement est une interfÃĐrence destructrice
de ces mÊmes ÃĐtats possibles.
On considÃĻre toutes les possibilitÃĐs pouvant arriver
au systÃĻme et qui se trouvent toutes incluses dans l'espace des ÃĐtats.
GÃĐomÃĐtriquement on peut reprÃĐsenter cela de la façon suivante:
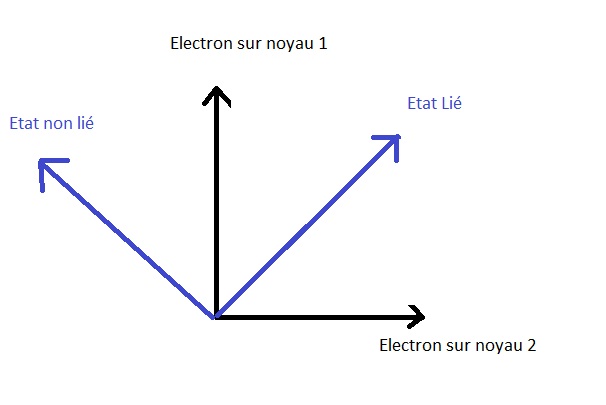
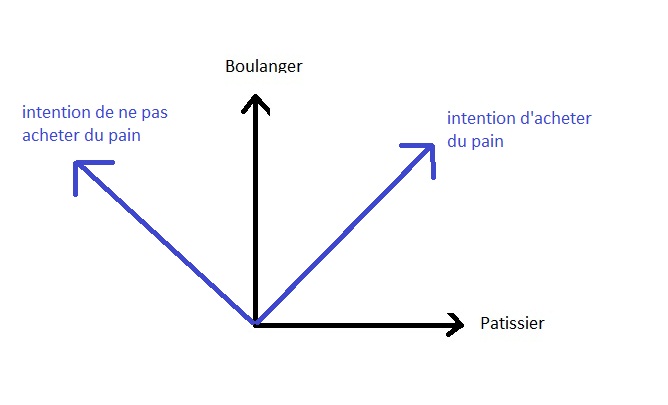
On remarque que les ÃĐtats d'ÃĐnergie observables (ÃĐtats de la molÃĐcule liÃĐ ou non liÃĐ)
sont aussi orthogonaux car ils correspondent à des options possibles pour l'ÃĐnergie mais
incompatibles entre elles.
L'ÃĐtat du systÃĻme (vecteur d'ÃĐtat) est lui-mÊme indÃĐpendant de sa reprÃĐsentation dans l'espace des ÃĐtats
soit par rapport à l'ÃĐnergie soit par rapport à la position.
On dit que les ÃĐtats propres liÃĐs à un opÃĐrateur sont une base de reprÃĐsentation du vecteur d'ÃĐtat (ici base bleue ou noire)
Ainsi on a pour le vecteur d'ÃĐtat une base de reprÃĐsentation pour l'opÃĐrateur position et une base de reprÃĐsentation
diffÃĐrente pour l'opÃĐrateur ÃĐnergie.
1.2.1.Non commutativitÃĐ des opÃĐrateurs quantiques: :20231119
1.2.2.Principe d'incertitude de Heisenberg
Le principe_d_incertitude_de_Heisenberg dÃĐcoule directement des postulats de la mÃĐcanique quantique.
On a vu qu'en gÃĐnÃĐral les ÃĐtats propres de deux observables ne sont pas reprÃĐsentÃĐs par les mÊmes vecteurs et qu'un ÃĐtat d'ÃĐnergie par exemple
sera reprÃĐsentÃĐ par une combinaison linÃĐaire (superposition) d'ÃĐtats de position s'ils ne commutent pas.
On comprend bien dans ce cas qu'il est impossible d'observer au cours d'une mÊme mesure d'un systÃĻme, à la fois la propriÃĐtÃĐ de position
et la propriÃĐtÃĐ d'ÃĐnergie puisque leurs ÃĐtats propres sont incompatibles. C'est à dire que les opÃĐrateurs ne commutent pas.
En pratique dans une expÃĐrience quantique, un grand nombre de particules sont observÃĐes, ce qui donne un rÃĐsultat statistique global
dans lequel il apparaÃŪt que plus on a de prÃĐcision sur la valeur de l'ÃĐnergie moins on a de prÃĐcision sur la position et vice-versa.
1.2.3.ReprÃĐsentation de la fonction d'onde dans l'espace physique
La diffÃĐrence entre le vecteur d'ÃĐtat et la fonction d'onde est le fait que le vecteur d'ÃĐtat
est indÃĐpendant de l'espace physique tandis que la fonction d'onde elle ne l'est pas parce qu'elle
se propage dans celui-ci.
En mÃĐcanique quantique on dit que la fonction d'onde est une projection du vecteur d'ÃĐtat dans l'espace physique.
Dans l'image ci-dessous on a reprÃĐsentÃĐ l'aspect ondulatoire (fonction d'onde) des ÃĐtats quantiques
afin de visualiser comment l'onde interfÃĻre destructrivement ou constructivement par addition ou soustraction.
Le fonctionnement fondamental d'une onde est le mÊme qu'il s'agisse d'une onde quantique, d'une onde
ÃĐlectromagnÃĐtique ou par exemple d'une onde à la surface d'un plan d'eau (vaguelettes).
Une onde prÃĐsente toujours une oscillation en creux et sommet (de la vague) autour d'une valeur moyenne (la surface plane de l'eau).
Les plus s'ajoutent entre eux (ainsi que les moins) et les plus et les moins se soustraient et s'annulent.
Par exemple si un creux de vague rencontre un sommet d'une autre vague, les deux s'annulent pour laisser
la surface de l'eau plane à l'endroit de la superposition.
1.2.3.1.ÃĐtats molÃĐcule hydrogÃĻne
Les ÃĐtats ondulatoires d'un atome ou d'une molÃĐcule correspondent à des ondes stationnaires
qui sont des ondes qui ne se propagent pas mais restent principalement localisÃĐes dans une rÃĐgion limitÃĐe
de l'espace, ici autour des noyaux d'hydrogÃĻne.

Le deuxiÃĻme postulat introduit donc les opÃĐrateurs qui s'appliquent sur les ÃĐtats pour les transformer.
On peut donc dire que le vecteur d'ÃĐtat reprÃĐsente l'aspect statique de la rÃĐalitÃĐ quantique,
tandis que l'opÃĐrateur reprÃĐsente l'aspect dynamique de cette mÊme rÃĐalitÃĐ.
Les troisiÃĻme, quatriÃĻme et cinquiÃĻme postulats dÃĐcrivent le processus mÊme de l'observation d'un systÃĻme quantique.
Mesure : valeurs possibles d'une observable
"La mesure d'une grandeur physique A ne peut donner qu'une valeur propre de l'observable A correspondante parmi toutes celles possibles."
Nous avons vu que les ÃĐtats observables d'une propriÃĐtÃĐ d'un systÃĻme quantique
ÃĐtaient nommÃĐs "ÃĐtats propres" (de cet observable).
A chaque "ÃĐtat propre" est associÃĐ une "valeur propre" qui est le rÃĐsultat de la mesure.
Par exemple pour la molÃĐcule d'hydrogÃĻne ce sera le niveau d'ÃĐnergie de la molÃĐcule
qui est diffÃĐrent si la molÃĐcule est dans son ÃĐtat liÃĐ ou non-liÃĐ.
Dans l'analogie du pain, on peut imaginer que le rÃĐsultat est le changement
du montant contenu dans le porte monnaie qui a diminuÃĐ lors de l'achat du pain.
La valeur propre est un nombre tandis que l'ÃĐtat propre est, comme nous l'avons vu, un vecteur.
Jusqu'à prÃĐsent nous n'avons utilisÃĐ du vecteur que sa direction qui est aussi associÃĐe à une dimension de l'espace des ÃĐtats
car c'est la notion la plus importante concernant l'ÃĐtat quantique.
En mathÃĐmatiques la valeur naturelle associÃĐe à un vecteur est sa longueur.
Cette longueur est abstraite (ce n'est pas l'espace physique donc on ne la mesure pas en mÃĻtres).
Pour cette raison on a crÃĐe un terme plus gÃĐnÃĐral se rapportant à la longueur ou l'ÃĐchelle d'oÃđ le non de "valeur scalaire".
Le scalaire est donc la valeur numÃĐrique associÃĐe à la longueur d'un vecteur.
Si on multiplie la longueur d'un vecteur par un nombre on obtiendra un vecteur dont la longueur sera un multiple de la valeur initiale,
il sera à une autre ÃĐchelle de grandeur, sa nouvelle valeur "scalaire".
Ici nous sommes donc en train d'observer l'ÃĐnergie du systÃĻme en utilisant donc l'opÃĐrateur ÃĐnergie.
On a vu que dans ce cas l'application de l'opÃĐrateur ÃĐnergie sur l'ÃĐtat donnait les deux ÃĐtats possibles d'ÃĐnergie simultanÃĐment:
H appliquÃĐ sur l' | ÃĐtat > donnera soit l'ÃĐtat | El > (pour liÃĐ) associÃĐ Ã l'ÃĐnergie El soit l'ÃĐtat | Enl > (pour non liÃĐ) associÃĐ Ã l'ÃĐnergie Enl
(les ÃĐnergies sont les valeurs propres de l'opÃĐrateur ÃĐnergie).
L'opÃĐrateur logique "ou" (ou non exclusif) est reprÃĐsentÃĐ en mÃĐcanique quantique dans l'espace des ÃĐtats par l'addition des vecteurs notÃĐe "+". On a donc:
H | ÃĐtat > = El | El > + Enl | Enl >
L'ÃĐtat global est une superposition des ÃĐtats propres possibles oÃđ El et Enl reprÃĐsentent comme on l'a vu respectivement les valeurs de l'ÃĐnergie des deux ÃĐtats.
Pour reprÃĐsenter le fait qu'une seule valeur est possible lors d'une mesure on utilise une propriÃĐtÃĐ des vecteurs que l'on appelle la projection.
Ci-dessous l'image de la projection de l'ÃĐtat global |Psy> sur l'ÃĐtat d'ÃĐnergie "molÃĐcule liÃĐe" | El >
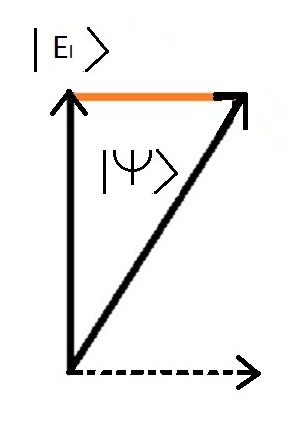
Lorsqu'on va effectuer la mesure de la propriÃĐtÃĐ physique sur le systÃĻme, le postulat dit que la mesure donne une valeur unique
et que cette valeur correspond à un ÃĐtat particulier du systÃĻme dit "ÃĐtat propre", la valeur obtenue ÃĐtant nommÃĐe "valeur propre".
Dans l'ÃĐquation prÃĐcÃĐdente on ajoute des possibilitÃĐs et non des valeurs, ainsi on n'a pas E = El + Enl, l'ajout de vecteur ne fonctionne pas comme l'ajout de valeur (scalaire).
On verra plus tard que l'ajout de possibilitÃĐs conduira non pas à la somme des ÃĐnergies mais à la valeur moyenne de l'ÃĐnergie qui est la somme des valeurs (ici El+Enl) divisÃĐe par le nombre
de valeurs ajoutÃĐes (ici 2). La valeur moyenne de l'ÃĐnergie serait donc E = (El+Enl)/2. En rÃĐalitÃĐ c'est un peu plus subtil que cela parce que la valeur moyenne de l'ÃĐnergie dÃĐpend
aussi de la probabilitÃĐ d'existence de chaque ÃĐtat d'ÃĐnergie, c'est donc une valeur moyenne pondÃĐrÃĐe par la probabilitÃĐ de chaque ÃĐtat.
C'est prÃĐcisÃĐment le sujet du quatriÃĻme postulat.
Postulat de Born : interprÃĐtation probabiliste de la fonction d'onde
"Lorsqu'on mesure la grandeur physique A sur un systÃĻme dans l'ÃĐtat "phi"
normÃĐ, la probabilitÃĐ P (An) d'obtenir la valeur propre An de l'observable A
correspondante est |Cn|Âē. OÃđ Cn est l'amplitude de la fonction d'onde projetÃĐe sur
l'ÃĐtat propre |phi n> correspondant à la valeur propre An observÃĐe.
Jusqu'Ã prÃĐsent nous avons seulement parlÃĐ des ÃĐtats, des ÃĐtats propres observables et de leurs valeurs propres associÃĐes.
Par convention la longueur d'un vecteur d'ÃĐtat quel qu'il soit vaut 1, la raison en est que le vecteur d'ÃĐtat vÃĐhicule l'existence du systÃĻme (premier postulat)
et qu'en terme de probabilitÃĐ, l'affirmation de l'existence du systÃĻme correspond à une certitude.
En probabilitÃĐ la certitude à la valeur 1.
Lorsque l'on a 1 chance sur 1 de quoi que se soit (1 divisÃĐ par 1 ÃĐgale 1) on est dans la certitude.
Une probabilitÃĐ infÃĐrieure à 1 est moins certaine que la certitude totale.
Par exemple, la chance de gagner au loto en ne jouant qu'une grille est de 1 divisÃĐ par quelques millions.
Ce qui fait que finalement un seul ou presque gagnera les millions au tirage !
Le tirage en terme quantique est "l'observation du gagnant".
L'amplitude de la fonction d'onde est la mÊme chose que la longueur du vecteur d'ÃĐtat.
Nous avons vu qu'un scalaire est une valeur numÃĐrique simple.
Lorsque l'on projette un vecteur sur un autre la longueur portÃĐe du premier sur le deuxiÃĻme est un nombre.
On a donc rÃĐalisÃĐ ainsi une opÃĐration qui à deux vecteurs associe un nombre que l'on appelle scalaire pour indiquer
que le rÃĐsultat particulier de cette opÃĐration de deux vecteurs ne donne pas un troisiÃĻme vecteur comme dans
l'addition des vecteurs mais un nombre (scalaire).
On appelle cette opÃĐration le produit scalaire:
Le produit scalaire est une opÃĐration qui à partir de deux vecteurs donne un nombre. Ce nombre est la longueur projetÃĐe orthogonalement d'un des vecteurs sur l'autre.
Le mot anglais "bracket" qui signifie crochet et qui fait rÃĐfÃĐrence aux caractÃĻres "<" et ">" Ces crochets sont utilisÃĐs traditionnellement en mathÃĐmatiques pour reprÃĐsenter la valeur moyenne d'une grandeur.
La valeur moyenne de l'ÃĐnergie sera notÃĐe par exemple < E >.
On a vu que l'ÃĐtat quantique ÃĐtait appelÃĐ aussi "ket" notÃĐ | ket >
l'autre partie du crochet est le "bra" qui est un opÃĐrateur particulier notÃĐ < bra |
C'est le physicien Paul_Dirac qui est à l'origine de cette sÃĐparation en deux
de ce mot pour faire apparaÃŪtre une dynamique d'opÃĐrateur et de vecteur dans l'opÃĐration de prise de la valeur moyenne.
Si on applique le "bra" sur le "ket" on obtient < bra | ket > ce qui est le nombre qui rÃĐsulte de l'application
de l'opÃĐrateur
On a ici une relation duale entre le bra et le ket.
Pour un ÃĐtat (ou ket) "| Psy >" le bra sera "< Psy |" la dualitÃĐ entre les deux est reprÃĐsentÃĐe comme l'image dans un miroir
Le ket est un vecteur tandis que le bra est un opÃĐrateur, l'application du bra sur le ket donne un nombre.
D'une maniÃĻre gÃĐnÃĐrale dans une expression ce qui est à droite du ket est un opÃĐrateur, le rÃĐsultat d'un opÃĐrateur
sur un ÃĐtat (vecteur) est soit un autre ÃĐtat (vecteur) soit un nombre qui reprÃĐsente un rÃĐsultat de mesure ou une probabilitÃĐ.
Pour tout ket il existe un bra correspondant et l'opÃĐration qui permet de passer du ket au bra s'appelle la conjugaison hermitique
et est notÃĐe par une ÃĐtoile. Ainsi ( | Psy > ) * = < Psy | ou (
ou |bra> = (ket>)*
Le bra est donc l'aspect dynamique (opÃĐrateur) du ket (ÃĐtat) qui produit la manifestation ( le rÃĐsultat de mesure ).
Ceci peut Être analogiquement rapprochÃĐ d'un aphorisme vÃĐdique faisant parler le crÃĐateur de l'univers:
"me retournant sur moi-mÊme, je crÃĐe encore et encore".
On peut aussi voir la mÊme forme dans le premier rÃĐcit de la crÃĐation de la GenÃĻse:
que la lumiÃĻre soit et la lumiÃĻre fÃŧt et D.ieu VIT que la lumiÃĻre ÃĐtait bonne.
< que la lumiÃĻre soit | et la lumiÃĻre fÃŧt > = et D.ieu VIT que la lumiÃĻre ÃĐtait bonne.
< soit | lumiÃĻreÂē | fÃŧt > = D.ieu VIT que la lumiÃĻre ÃĐtait bonne.
Le fait que D.ieu vit que la lumiÃĻre ÃĐtait bonne est clairement le rÃĐsultat d'une observation.
On pourrait appeler tout cela l'alphabet et la syntaxe quantique.
L'alphabet ne se compose que d'une lettre | Psy > et c'est "l'Être" (ou l'ÃĐtat qui est l'affirmation de l'Être)
L'opÃĐration duale * fait apparaÃŪtre sa valeur dynamique d'opÃĐrateur ( | Psy > )* = < Psy |
Toutes leurs combinaisons font apparaÃŪtre la grammaire quantique.
Un exemple est l'application de l'opÃĐrateur < Psy | sur l'ÃĐtat | Psy > donne < Psy|Psy > qui est aussi la projection
de l'ÃĐtat |Psy> sur lui-mÊme et qui vaut donc 1. Ce qui peut se traduire de maniÃĻre triviale par la phrase:
"Psy participe à 100% (100/100=1) à Psy".
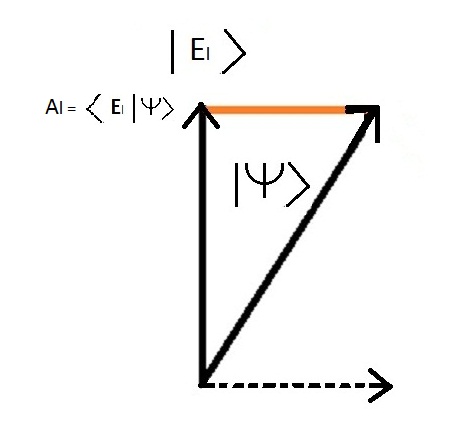
< Psy L | Psy > est quand à lui la projection de l'ÃĐtat gÃĐnÃĐral du systÃĻme sur l'ÃĐtat ÃĐnergÃĐtique liÃĐ de l'exemple de la molÃĐcule H2+
et reprÃĐsente l'amplitude de probabilitÃĐ d'obtenir l'ÃĐtat liÃĐ lors d'une observation.
Al = < Psy L | Psy >
En prenant le carrÃĐ de l'amplitude on obtient la probabilitÃĐ
La probabilitÃĐ de l'ÃĐtat | Psy L > est: Pl = AlÂē = ( < Psy L | Psy > )Âē
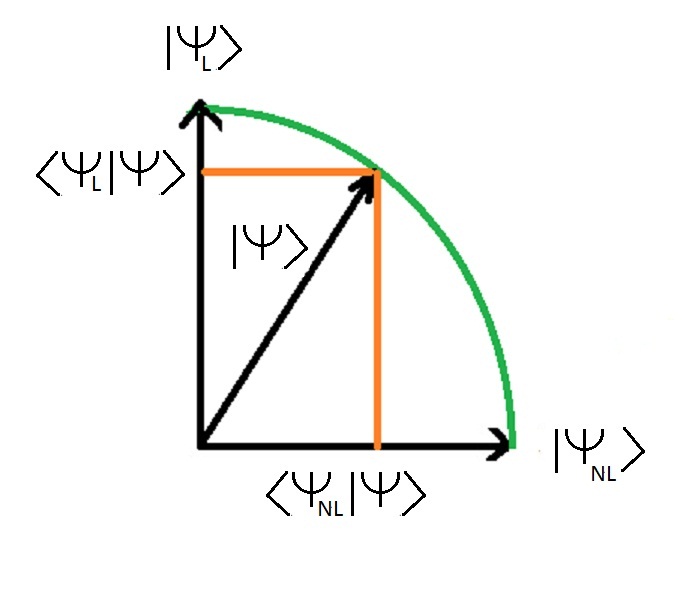
L'image ci-dessous reprÃĐsente la projection de l'ÃĐtat gÃĐnÃĐral | Psy > sur les deux ÃĐtats d'ÃĐnergie | Psy l > et | Psy nl >
(qui sont la mÊme chose que les ÃĐtats | El > et | Enl > c'est juste une diffÃĐrence de notation)
Les deux valeurs < Psy l | Psy > et < Psy nl | Psy > reprÃĐsentent la longueur de l'ÃĐtat | Psy > (qui vaut 1) projetÃĐ sur les ÃĐtats propres | Psy l > et | Psy nl >
< Psy l | Psy > est la projection de l'ÃĐtat | Psy > sur l'ÃĐtat propre | Psy l >
< Psy nl | Psy > est la projection de l'ÃĐtat | Psy > sur l'ÃĐtat propre | Psy nl >
Lorsque nous avons considÃĐrÃĐ les ÃĐtats "acheter du pain" |boulanger> et |pÃĒtissier>
nous avons implicitement considÃĐrÃĐ que nous pouvions observer l'un et l'autre
de maniÃĻre indiffÃĐrente, c'est à dire ayant une probabilitÃĐ d'advenir ÃĐgale.
Mais les caractÃĐristiques du systÃĻme peuvent Être telles que ce n'est pas le cas,
par exemple si le boulanger est plus proche du domicile que le pÃĒtissier et qu'il
fait trÃĻs froid la probabilitÃĐ de l'ÃĐtat |boulanger> sera plus forte que celle
de l'ÃĐtat |pÃĒtissier>.
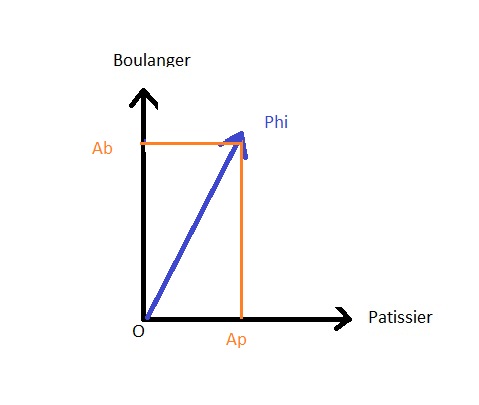
C'est ce qui est reprÃĐsentÃĐ dans l'image ci-dessous oÃđ Ab est supÃĐrieur à Ap. (A est l'amplitude de probabilitÃĐ).
La projection de l'ÃĐtat |Phi> gÃĐnÃĐral sur l'ÃĐtat |boulanger> a la valeur Ab
qui correspond à l'amplitude de probabilitÃĐ d'obtenir cet ÃĐtat à partir de
l'ÃĐtat gÃĐnÃĐral |Phi> de la mÊme façon pour Ap qui est l'amplitude de probabilitÃĐ
d'obtention de l'ÃĐtat |pÃĒtissier>.
Les ÃĐtats propres quantiques sont toujours orthogonaux c'est à dire qu'ils sont
à angle droit et donc suivent la thÃĐorÃĻme de Pythagore
pour le triangle rectangle.
"La somme du carrÃĐ des longueurs des deux cÃītÃĐs est ÃĐgale au carrÃĐ de la longueur de l'hypotÃĐnuse"
Dans notre cas l'hypotÃĐnuse correspond au vecteur d'ÃĐtat |phi> et les deux cÃītÃĐs aux projections
de |phi> sur les deux ÃĐtats propres |boulanger> et | Epicier>.
Le postulat dit que le carrÃĐ de l'amplitude de l'onde est la probabilitÃĐ.
Le fait de considÃĐrer l'ÃĐtat gÃĐnÃĐral du systÃĻme revient à simplement considÃĐrer qu'il existe:
la probabilitÃĐ de l'ÃĐtat effectif du systÃĻme est donc toujours ÃĐgal à 1.
C'est ce que le postulat mentionne en disant que l'ÃĐtat |phi> est normÃĐ et sa norme est toujours
ÃĐgale à 1 par convention puisqu'il s'agit d'une probabilitÃĐ.
MathÃĐmatiquement on note < phi | phi > = 1 = | |phi> | Âē
(la derniÃĻre expression reprÃĐsente le carrÃĐ de la norme du vecteur, la norme du vecteur ÃĐtant sa longueur)
Ensuite cette probabilitÃĐ se divise en plusieurs probabilitÃĐs infÃĐrieures correspondant à chaque
ÃĐtat propre mais avec la contrainte que la somme des carrÃĐs des amplitudes des ÃĐtats propres
du systÃĻme est toujours ÃĐgale à 1 qui est la probabilitÃĐ certaine.
AbÂē+ ApÂē = 1
La somme des probabilitÃĐs de tous les ÃĐtats possibles du systÃĻme doit Être ÃĐgale à 1.
On peut dire que l'existence du systÃĻme se rÃĐpartit sur toutes ses possibilitÃĐs d'exister
mais sans qu'il y ait de perte d'existence afin que son existence soit conservÃĐe.
En effet si la probabilitÃĐ totale diminuait cela voudrait dire que le systÃĻme aurait
moins de chance d'exister et en rÃĐduisant la probabilitÃĐ de son existence à zÃĐro,
celui-ci disparaÃŪtrait !
L'amplitude de l'ÃĐtat ou fonction d'onde peut-Être positive ou nÃĐgative exactement comme
on peut avoir la crÊte ou le creux d'une vague.
L'amplitude de probabilitÃĐ est donc soit nÃĐgative soit positive, c'est ce que nous avons
reprÃĐsentÃĐ dans l'image sur les ÃĐtats liÃĐs et non-liÃĐs de la molÃĐcule d'hydrogÃĻne
par les symboles plus + et moins - . (ÃĐtats molÃĐcule hydrogÃĻne)
Mais la probabilitÃĐ qui est le carrÃĐ de l'amplitude (ou carrÃĐ de la norme )
est donc toujours positive ce qui est normal pour une probabilitÃĐ.
En effet on peut imaginer une probabilitÃĐ certaine, puis moins certaine
jusqu'Ã peu certaine voire nulle mais une probabilitÃĐ nÃĐgative n'a pas de sens.
Par contre l'amplitude de probabilitÃĐ elle, peut Être nÃĐgative.
Supposons alors que l'on ait deux amplitudes de probabilitÃĐ ÃĐgales
mais de signes opposÃĐs se propageant l'une vers l'autre (ce sont des ondes).
Si l'on considÃĻre les probabilitÃĐs lorsque ces amplitudes se trouvent
au mÊme endroit alors les amplitudes de signes opposÃĐs s'annulent
et leur carrÃĐ est aussi nul. La probabilitÃĐ d'observer quelque chose
sera nulle.
Mais si les amplitudes sont sÃĐparÃĐes leur carrÃĐ sera positif
(plus par plus est positif mais moins par moins est aussi positif)
et donc la probabilitÃĐ d'observer quelque chose ne sera plus nulle.
Lorsqu'on parle de mÃĐcanique quantique on pense à son caractÃĻre probabiliste comme un jeu de hasard
mais ce que l'on ignore gÃĐnÃĐralement c'est que ces probabilitÃĐs sont sous-tendues par quelque chose
de beaucoup plus troublant qui est l'amplitude de l'onde de probabilitÃĐ et qui donne
toute sa rÃĐalitÃĐ Ã la mÃĐcanique quantique.
Si on considÃĻre l'expression | Psy L >< Psy L | composÃĐe d'un ket puis d'un bra et qu'on l'applique au ket | Psy > on obtient
| Psy L >< Psy L | Psy > oÃđ < Psy L | Psy > est l'amplitude de probabilitÃĐ d'obtenir l'ÃĐtat | Psy L >
on a donc :
| Psy L >< Psy L | Psy > = | Psy L > Al = Al | Psy L >
on voit que l'ÃĐtat final est l'ÃĐtat | Psy L > associÃĐ Ã la probabilitÃĐ Al
L'expression | Psy L >< Psy L | est donc un opÃĐrateur qui a fait ÃĐvoluer l'ÃĐtat initial | Psy > vers l'ÃĐtat final | Psy L >
et ceci avec une probabilitÃĐ Al.
C'est un opÃĐrateur d'ÃĐvolution qui a fait ÃĐvoluer le systÃĻme vers l'ÃĐtat d'ÃĐnergie liÃĐ lors d'une observation.
Ceci nous amÃĻne naturellement vers le cinquiÃĻme postulat qui dÃĐcrit comment le systÃĻme ÃĐvolue lors d'une mesure.
1.3.2.OpÃĐrateur partition de l'unitÃĐ
ConsidÃĐrons l'opÃĐrateur suivant:
| Psy L >< Psy L | + | Psy nl >< Psy nl |
qui est la somme des opÃĐrateurs d'ÃĐvolution vers les ÃĐtats propres d'une observable (ici l'ÃĐnergie : ÃĐtat liÃĐ et non-liÃĐ).
( | Psy L >< Psy L | + | Psy nl >< Psy nl | ) | Psy >
ou
| Psy L >< Psy L | Psy > + | Psy nl >< Psy nl | Psy >
ce qui donne
| Psy L > Al + | Psy nl > Anl
ou encore
Al | Psy L > + Anl | Psy nl >
ce qui est la dÃĐcomposition de l'ÃĐtat | Psy > en somme de ses ÃĐtats propres d'ÃĐnergie
| Psy > = Al | Psy L > + Anl | Psy nl >
L'opÃĐrateur n'a pas changÃĐ l'ÃĐtat | Psy > mais l'a simplement dÃĐcomposÃĐ en ces diffÃĐrentes parties,
pour cette raison on l'appelle opÃĐrateur "partition de l'unitÃĐ".
Il est intÃĐressant de constater comment la reprÃĐsentation vectorielle de l'ÃĐtat et sa dÃĐcomposition
suivant une base orthogonale permet de reprÃĐsenter naturellement les amplitudes de probabilitÃĐs et par lÃ
les probabilitÃĐs de l'ÃĐvolution du systÃĻme lors d'une mesure.
Mesure : rÃĐduction du paquet d'onde
Si la mesure de la grandeur physique A, Ã l'instant t, sur un systÃĻme reprÃĐsentÃĐ par le vecteur |phi> donne comme rÃĐsultat la valeur propre
An alors l'ÃĐtat du systÃĻme immÃĐdiatement aprÃĻs la mesure est projetÃĐ sur le sous-espace propre associÃĐ Ã An
Ce postulat est aussi appelÃĐ "postulat de rÃĐduction du paquet d'onde".
Tout d'abord ÃĐlucidons cette notion de "sous-espace propre". Il s'agit juste d'une gÃĐnÃĐralisation de la dÃĐcomposition de l'ÃĐtat
dans ses ÃĐtats propres. Reprenons l'exemple du pain avec deux boulangers et un pÃĒtissier.
Si la distinction du type de commerce n'est pas observable (n'est pas une observable du systÃĻme), il n'y aura pas lieu de distinguer
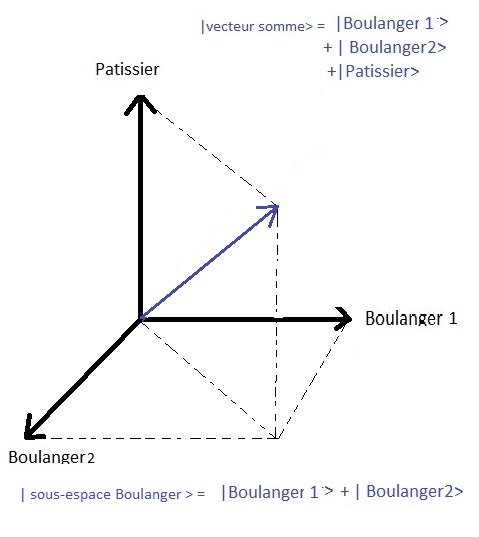
si il s'agit du boulanger 1 ou du boulanger 2 lors d'une mesure, on se contentera de savoir que l'ÃĐtat a ÃĐtÃĐ projetÃĐ vers le sous-espace
propre boulanger qui correspond en fait, dans le schÃĐma ci-dessous, au plan horizontal peuplÃĐ par les boulangers !
Si il existait une observable qui permette d'observer chez quel boulanger le pain a ÃĐtÃĐ achetÃĐ, lors de cette
mesure l'ÃĐtat serait projetÃĐ vers l'un ou l'autre des boulangers, levant l'indÃĐtermination lors de la mesure.
En pratique lorsque plusieurs ÃĐtats propres ont la mÊme valeur propre (mÊme ÃĐnergie) ont dit que
ces ÃĐtats sont dÃĐgÃĐnÃĐrÃĐs. En appliquant au systÃĻme une contrainte d'ÃĐnergie supplÃĐmentaire qui va modifier
l'ÃĐnergie des ÃĐtats dÃĐgÃĐnÃĐrÃĐs de façon qu'il n'y ait plus d'ÃĐgalitÃĐ on lÃĻvera la dÃĐgÃĐnÃĐrescence.
La physique quantique s'occupe essentiellement de comprendre la structure du monde microscopique
qui est essentiellement constituÃĐ de rÃĐsonances (ondes stationnaires) qui sont des ÃĐtats propres de l'opÃĐrateur ÃĐnergie totale
du systÃĻme (Hamiltonien).
Le cinquiÃĻme postulat dit que lors de la mesure, l'ÃĐtat du systÃĻme ÃĐvolue vers l'ÃĐtat dont la valeur propre a ÃĐtÃĐ mesurÃĐe.
C'est ce postulat dit de "rÃĐduction du paquet d'onde" ou de "collapse de la fonction d'onde" qui donne à la reprÃĐsentation
gÃĐomÃĐtrique de projection d'un vecteur sa rÃĐalitÃĐ physique, puisque le systÃĻme ÃĐvolue physiquement dans cette opÃĐration.
C'est probablement la plus grande rÃĐvolution conceptuelle de la mÃĐcanique quantique d'introduire le fait que l'observation du systÃĻme le fait ÃĐvoluer
alors que dans les thÃĐories physiques non-quantiques c'est seulement l'ÃĐquation dynamique qui est responsable de l'ÃĐvolution du systÃĻme.
Traditionnellement l'ÃĐquation dynamique d'une thÃĐorie mÃĐcanique exprime comment l'ÃĐnergie agit sur le systÃĻme pour le transformer.
Dans le cas de la mÃĐcanique quantique une telle ÃĐquation dynamique existe aussi et elle s'appelle l'ÃĐquation de Shroedinger .
On a donc en mÃĐcanique deux mÃĐcanismes pour l'ÃĐvolution: l'action de l'ÃĐnergie dans le temps et l'action de l'observation hors du temps.
C'est cette ÃĐquation qui constitue le sixiÃĻme et dernier postulat de la mÃĐcanique quantique (voir ci-aprÃĻs).
Le cinquiÃĻme postulat quant à lui implique l'observateur du systÃĻme dans l'ÃĐvolution du systÃĻme.
Ainsi en mÃĐcanique quantique l'observateur n'est plus indÃĐpendant du systÃĻme physique.
L'observateur et le systÃĻme physique forment un ensemble indissociable.
On pourrait dire que l'observateur est intriquÃĐ dans le systÃĻme (mais pas au sens de l'intrication quantique qui ne concerne que la fonction d'onde).
On a ÃĐvoquÃĐ plus haut le phÃĐnomÃĻne de l'intrication quantique qui provient du fait qu'un systÃĻme quantique formÃĐ de plusieurs
particules est dÃĐcrit par une fonction d'onde unique (premier postulat) mÊme si les particules sont susceptibles de s'Être ÃĐloignÃĐes dans l'espace physique.
C'est cette implication de la mÃĐcanique quantique qu'Einstein n'a officiellement jamais pu admettre parce qu'Ã son sens elle violait
la limite de propagation de toute interaction physique dÃĐfinie par la vitesse de la lumiÃĻre. Selon la thÃĐorie de la relativitÃĐ d'Einstein
aucune ÃĐnergie ne peut se dÃĐplacer plus vite que la vitesse de la lumiÃĻre. La lumiÃĻre se dÃĐplace ÃĐvidemment à la vitesse de la lumiÃĻre
et elle ne peut faire cela que parce qu'elle est une ÃĐnergie pure, c'est à dire sans masse. Les particules massiques doivent donc forcÃĐment
se dÃĐplacer à une vitesse infÃĐrieure à celle de la lumiÃĻre.
La rÃĐsolution "physique" de ce paradoxe quantique a ÃĐtÃĐ effectuÃĐ par une expÃĐrimentation connue sous le nom d'expÃĐrience_d_Aspect.
On dit que la thÃĐorie quantique est une thÃĐorie non-locale. Les termes utilisÃĐs "non-localitÃĐ" ou "non-sÃĐparabilitÃĐ" sont ÃĐquivalents.
On peut donc dire que la fonction d'onde quantique transcende l'espace physique, elle transcende mÊme l'espace-temps puisque
depuis la thÃĐorie de la relativitÃĐ d'Einstein on doit considÃĐrer l'espace et le temps comme ÃĐtant les aspects d'une
mÊme rÃĐalitÃĐ plus profonde : le continuum espace-temps. Une expÃĐrience plus rÃĐcente effectuÃĐe dans un cadre relativiste et
menÃĐe dans la continuitÃĐ de l'expÃĐrience d'Aspect a confirmÃĐ la validitÃĐ de l'intrication quantique dans le cadre relativiste.
( cf ExpÃĐrience_d_Antoine_Suarez trouvÃĐe sur le site du physicien
Philippe_Guillemant qui offre une vision intÃĐgrant la rÃĐalitÃĐ quantique )
Cette derniÃĻre expÃĐrience est importante car dans une expÃĐrience de physique on ne peut mesurer que des valeurs dans un certain
intervalle. Ainsi dans la premiÃĻre expÃĐrience d'Aspect les dÃĐtecteurs des photons corrÃĐlÃĐs (dans un ÃĐtat quantique unique)
n'ÃĐtaient sÃĐparÃĐs que de quelques mÃĻtres. Cela ÃĐtait suffisant pour dÃĐmontrer que l'intrication quantique ne pouvait pas
Être due à un phÃĐnomÃĻne physique ignorÃĐ (variable cachÃĐe) s'effectuant à une vitesse infra luminique. La vitesse d'un tel
phÃĐnomÃĻne serait forcement supraluminique. Bien qu'une telle vitesse supraluminique soit difficilement acceptable à cause
de la thÃĐorie de la relativitÃĐ d'Einstein, la premiÃĻre expÃĐrience d'Aspect ne permettait pas de rÃĐvoquer complÃĻtement
cette possibilitÃĐ. Avec l'expÃĐrience d'Antoine Suarez c'est chose faite parce que c'est mÊme la possibilitÃĐ d'une causalitÃĐ
entre les dÃĐtections des deux photons corrÃĐlÃĐs qui est supprimÃĐe, parce que les rÃĐfÃĐrentiels relativistes dans lesquels sont
faites les dÃĐtections, ne permettent pas un "avant" et "aprÃĻs", condition essentielle pour une causalitÃĐ: aucun des deux photons
n'est dÃĐtectÃĐ avant ou aprÃĻs l'autre car ces dÃĐtections ne sont pas faites dans les mÊmes rÃĐfÃĐrentiels temporels.
Dans une thÃĐorie quantique relativiste la fonction d'onde ne peut donc plus dÃĐpendre du temps comme on l'a vu dans le premier
postulat. La raison en est que le temps est ramenÃĐ au mÊme niveau que la position c'est à dire une propriÃĐtÃĐ observable du systÃĻme,
et que la fonction d'onde est indÃĐpendante des propriÃĐtÃĐs du systÃĻme (deuxiÃĻme postulat).
L_expÃĐrience_du_chat_de_Shroedinger est une expÃĐrience de pensÃĐe
imaginÃĐe par le physicien Erwin_Shroedinger pour rÃĐflÃĐchir
sur le problÃĻme de la mesure en mÃĐcanique quantique directement liÃĐ avec le cinquiÃĻme postulat.
Vous avez pu constater dans les postulats consacrÃĐs à la mesure (ou observation) que l'on ne rentre pas en dÃĐtail de ce qu'est l'observateur.
Les postulats disent qu'il y a bien un observateur qui fait la mesure mais ne disent rien de plus sur la nature de l'observateur !
Dans cette expÃĐrience, un chat est isolÃĐ dans un caisson de façon à ce qu'on ne puisse l'observer (quantiquement) d'aucune maniÃĻre.
Cela suppose que le chat peut Être considÃĐrÃĐ comme un objet quantique, ce qui n'est pas le cas en pratique bien qu'en thÃĐorie
le chat puisse Être considÃĐrÃĐ Ã priori comme un systÃĻme physique, ÃĐtant composÃĐ d'atomes qui eux le sont et sont bien dÃĐcrits
par la mÃĐcanique quantique.
Dans ce caisson se trouve aussi une fiole contenant un gaz mortel pour le chat et un dÃĐtecteur de particules qui ouvre la
fiole en cas de dÃĐtection d'une particule.
Si une particule est dÃĐtectÃĐe le chat sera mort, si elle n'est pas dÃĐtectÃĐe le chat sera vivant.
Tant que l'on n'a pas observÃĐ l'ÃĐtat de santÃĐ du chat "quantique" celui-ci reste dans un ÃĐtat quantique gÃĐnÃĐral dit de superposition
des ÃĐtats propres observables, que sont | chat vivant > et | chat mort >
on a donc | chat > = | chat vivant > + | chat mort >
Notre systÃĻme quantique est formÃĐ de plusieurs composantes: le chat, le dÃĐtecteur, la particule.
Tout ces sous-systÃĻmes doivent aussi Être considÃĐrÃĐs dans l'ÃĐtablissement de la fonction d'onde, on a donc:
| particule > = | particule prÃĐsente > + | particule absente >
et
| dÃĐtecteur > = | ÃĐtat particule dÃĐtectÃĐe > + | ÃĐtat particule non-dÃĐtectÃĐe >
Les mathÃĐmatiques associÃĐes à la mÃĐcanique quantique montrent que le systÃĻme global que l'on appellera "shroedinger" est :
| shroedinger > = | chat, dÃĐtecteur, particule > = | chat> ÂĪ | dÃĐtecteur > ÂĪ | particule >
oÃđ ÂĪ reprÃĐsente le "produit tensoriel" des vecteurs d'ÃĐtat.
Se retrouvant au sein d'un mÊme ÃĐtat quantique, on dit que ces diffÃĐrents sous-systÃĻmes sont intriquÃĐs.
Ce produit se comporte comme une opÃĐration de produit habituel, il est distributif : A * ( B + C ) = A*B + A*C
En terme quantique on peut donc dÃĐvelopper l'ÃĐtat quantique gÃĐnÃĐral. Commençons seulement par le systÃĻme composÃĐ uniquement du dÃĐtecteur
et de la particule.
| dÃĐtecteur, particule > = | dÃĐtecteur > ÂĪ | particule > = ( | ÃĐtat particule dÃĐtectÃĐe > + | ÃĐtat particule non-dÃĐtectÃĐe > ) ÂĪ ( | particule prÃĐsente > + | particule absente > )
en dÃĐveloppant :
Les deux premiers ÃĐtats sont facilement comprÃĐhensibles, si la particule est prÃĐsente il est logique qu'elle soit dÃĐtectÃĐe et qu'elle ne le soit pas si elle est absente.
Les deux ÃĐtats suivants sont trÃĻs improbables mais existent nÃĐanmoins d'aprÃĻs la mÃĐcanique quantique pour laquelle tout n'est qu'amplitude de probabilitÃĐ.
Pour l'ÃĐtat | shroedinger > complet il faudrait encore dÃĐvelopper avec les ÃĐtats du chat ce qui nous amÃĻnerait à une fonction d'onde comportant huit ÃĐtats propres possibles
dont deux fort probables et six fortement improbables.
Les deux ÃĐtats probables sont:
| chat mort > ÂĪ | ÃĐtat particule dÃĐtectÃĐe > ÂĪ | particule prÃĐsente >
| chat vivant > ÂĪ | ÃĐtat particule non-dÃĐtectÃĐe > ÂĪ | particule absente >
Tant que l'on n'a pas observÃĐ le systÃĻme, ce qui correspond par exemple à ouvrir la boite, on est dans un ÃĐtat de superposition
oÃđ le chat est dans un ÃĐtat vital indÃĐterminÃĐ. C'est là que se trouve le paradoxe.
Mais on peut pousser le raisonnement plus loin et c'est ce qu'Ã fait le physicien EugÃĻne_Wigner prix Nobel de physique.
Il s'agit de la thÃĐorie_de_l_influence_de_la_conscience
Il a considÃĐrÃĐ que l'oeil de l'observateur qui voit le chat mort ou vivant est aussi un systÃĻme quantique avec deux ÃĐtats:
| oeil > = | oeil voit le chat mort > + | oeil voit le chat vivant >
Les ÃĐtats de la fonction d'onde complÃĻte prendraient alors en compte des ÃĐtats "hallucinatoires" oÃđ l'oeil verrait mort, le chat vivant...
Mais on pourrait ainsi continuer à considÃĐrer la chaÃŪne de la mesure jusqu'au cerveau de l'observateur qui est ÃĐgalement composÃĐ d'atomes.
Donc la question est : à quel moment se rÃĐalise effectivement la mesure c'est à dire le collapse de la fonction d'onde et donc le choix
du rÃĐsultat de l'expÃĐrience: chat mort ou vivant.
Wigner dit que rien de matÃĐriel ne peut provoquer le collapse parce que toute la matÃĐrialitÃĐ est susceptible d'Être dÃĐcrite par la
mÃĐcanique quantique et donc fait partie de la fonction d'onde et on peut ÃĐgalement trÃĻs bien considÃĐrer la fonction d'onde de l'univers.
Dans son interprÃĐtation L'observateur est la conscience .
On peut remarquer le lien qui existe entre l'observateur et la fonction d'onde: aucun des deux n'est matÃĐriel !
On pourrait dire que ce qui est matÃĐriel est ce qui se trouve entre les deux: l'observation.
Ceci nous rapproche de la conception de la "rÃĐalitÃĐ indÃĐpendante" ou du "rÃĐel voilÃĐ" introduit par le physicien
Bernard_d_Espagnat pour la comprÃĐhension philosophique de la mÃĐcanique quantique.
Ceci nous rapproche ÃĐgalement de la conception vÃĐdique, dans l'Inde ancienne, de la rÃĐalitÃĐ matÃĐrielle dÃĐcrite comme "Maya" ou l'illusion des sens.
L'observateur conscience et la rÃĐalitÃĐ quantique non-matÃĐrielle crÃĐe la rÃĐalitÃĐ matÃĐrielle phÃĐnomÃĐnologique.
A ce titre le film Matrix reprÃĐsente bien une allÃĐgorie de la rÃĐalitÃĐ, la seule diffÃĐrence, et elle est importante,
vient du fait que ce ne sont pas des machines qui crÃĐent la rÃĐalitÃĐ illusoire mais la conscience elle-mÊme.
Ainsi on peut dÃĐfinir la conscience comme ÃĐtant la mise en relation du sujet avec l'objet par la perception ou connaissance.
La fonction d'onde et la conscience reprÃĐsentent les deux faces d'une mÊme rÃĐalitÃĐ transcendant la matÃĐrialitÃĐ et
à l'origine mÊme de cette matÃĐrialitÃĐ.
ÃĐvidemment les physiciens dans leur ensemble ne vont gÃĐnÃĐralement pas aussi loin dans la vision de la rÃĐalitÃĐ quantique.
La position standard dans ce domaine est l'interprÃĐtation_de_l_ÃĐcole_de_Copenhague.
Cette position ÃĐmerge de la situation de l'observateur humain qui expÃĐrimente un monde classique et le considÃĻre comme la rÃĐfÃĐrence absolue.
On peut dÃĐfinir diffÃĐrents degrÃĐs d'ÃĐloignement de cette position:
Il faut remarquer que ce point de vue n'est plus tenable scientifiquement depuis l'expÃĐrience d'Aspect qui valide la mÃĐcanique
quantique dans ses affirmations les plus troublantes.
En mÊme temps cette mÃĐcanique quantique est la thÃĐorie la plus vÃĐrifiÃĐe de l'histoire des sciences.
Ce point de vue est donc ainsi ramenÃĐ Ã une simple "croyance matÃĐrialiste".
Ce point de vue ÃĐtait nÃĐanmoins celui d'Einstein mais il n'a malheureusement pas vÃĐcu suffisamment longtemps pour
voir la rÃĐsolution par l'expÃĐrience d'Aspect, du paradoxe qu'il a dÃĐfinit avec les physiciens Podolsky et Rosen dans son fameux article:
le Paradoxe_EPR.
Ici le monde classique dans lequel nous vivons ne reprÃĐsente plus la totalitÃĐ du monde car il existe
un monde quantique absolument ÃĐtrange auquel nous n'avons pas accÃĻs mais avec qui nous pouvons traiter par
l'intermÃĐdiaire de la thÃĐorie quantique.
Le monde physique stable que nous connaissons est constituÃĐ uniquement de trois particules quantiques: ÃĐlectron, proton et neutrino.
Ce troisiÃĻme point de vue lÃĻve tous les paradoxes quantiques en disant finalement et simplement qu'il ne faut
pas chercher une interprÃĐtation (classique) de la thÃĐorie quantique mais qu'il faut simplement l'accepter
telle qu'elle est (Copenhague) et finalement reconnaÃŪtre la suprÃĐmatie de sa position.
On peut ainsi prÃĐdire que le modÃĻle quantique ne sera jamais mis en dÃĐfaut. Depuis sa crÃĐation on voit de plus en plus à quel point la rÃĐalitÃĐ quantique
intervient dans la comprÃĐhension du monde qui nous entoure et plus particuliÃĻrement dans le domaine du vivant, systÃĻme macroscopique d'une grande cohÃĐrence... quantique.
Voici deux exemples assez rÃĐcents:
Le problÃĻme central ou pivot entre la rÃĐalitÃĐ quantique et la rÃĐalitÃĐ classique est celui de la dÃĐcohÃĐrence.
La dÃĐcohÃĐrence est le passage d'un fonctionnement quantique à un fonctionnement classique.
Lorsque l'on ÃĐtudie la mÃĐcanique quantique, on nous montre que celle-ci se rÃĐduit aux lois de la mÃĐcanique
classique lorsqu'on la considÃĻre aux ÃĐchelles macroscopiques.
La dÃĐcohÃĐrence est le fait de passer de la description du systÃĻme physique par une fonction d'onde unique
à celui d'un ensemble sÃĐparÃĐ de corpuscules.
La thÃĐorie physique qui s'occupe de dÃĐcrire un ensemble important de corpuscules est la thermodynamique
statistique qui prend ses fondements dans la thÃĐorie quantique à travers les statistiques quantiques de
BÃķse-Einstein et de Fermi-Dirac.
Cette thÃĐorie constituÃĐe au 20iÃĻme siÃĻcle permet de retrouver à partir de considÃĐrations microscopiques
les rÃĐsultats de la thermodynamique macroscopique du 19iÃĻme siÃĻcle.
La thermodynamique opÃĻre dans le monde classique de la dÃĐcohÃĐrence tandis que la mÃĐcanique quantique
opÃĻre dans le monde quantique de la cohÃĐrence ondulatoire.
La dÃĐcohÃĐrence est le passage du monde quantique au monde classique.
MaÃŪtriser la dÃĐcohÃĐrence est le challenge pour produire l'ordinateur quantique.
Alain Aspect dans sa confÃĐrence Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_rÃĐvolution_quantique
admet à ce sujet (à 1H23mn) que si l'ordinateur quantique peut un jour devenir une rÃĐalitÃĐ, il ne voit pas pourquoi le cerveau ne pourrait pas en Être un.
Ainsi les deux rÃĐalitÃĐs non-physiques: la conscience et la fonction d'onde pourraient n'en Être en rÃĐalitÃĐ qu'une seule.
ÃĐvolution temporelle de l'ÃĐtat quantique.
L'ÃĐtat Phi
de tout systÃĻme quantique non-relativiste est une solution de l'ÃĐquation
de SchrÃķdinger dÃĐpendante du temps:
Le sixiÃĻme postulat est l'ÃĐquation de Schroedinger
.
C'est l'ÃĐquation dynamique de la mÃĐcanique quantique.
Elle signifie simplement que c'est l'opÃĐrateur ÂŦ ÃĐnergie totale Âŧ du systÃĻme ou hamiltonien notÃĐ "H", qui est responsable de l'ÃĐvolution du systÃĻme dans le temps.
(Traditionnellement en mÃĐcanique quantique on fait porter un chapeau aux opÃĐrateurs pour les distinguer des autres objets mathÃĐmatiques comme les valeurs propres.)
La forme de l'ÃĐquation montre qu'en appliquant l'opÃĐrateur hamiltonien à la fonction d'onde du systÃĻme, on obtient sa dÃĐrivÃĐe par rapport
au temps c'est-Ã -dire comment elle varie dans le temps.
(pour une variation delta t du temps donc "dt" on a une variation "d | Psy(t) >" de la fonction d'onde).
Donc si on applique l'opÃĐrateur hamiltonien (ÃĐnergie) Ã la fonction d'onde on obtient son ÃĐvolution dans le temps.
Cette ÃĐquation n'est valable que dans le cadre non relativiste.
Dans le cadre relativiste l'ÃĐquation valable est l'ÃĐquation de Klein-Gordon.
L'opÃĐrateur hamiltonien H est composÃĐ de toutes les ÃĐnergies qui interviennent sur le systÃĻme.
Ces ÃĐnergies sont de deux ordres: l'ÃĐnergie cinÃĐtique et l'ÃĐnergie potentielle.
L'ÃĐnergie cinÃĐtique est celle contenue dans une masse en mouvement. Un caillou jetÃĐ dans une vitre la casse en vertu de l'ÃĐnergie
cinÃĐtique qu'elle a acquise lorsqu'on lui a donnÃĐ une certaine vitesse. Si il y a plusieurs vitres successives, plus la vitesse du caillou
sera grande et plus il traversera de vitres.
L'ÃĐnergie potentielle est due aux champs de forces qui s'appliquent sur le systÃĻme. Si on laisse tomber un caillou sur une vitre au sol
celui-ci va acquÃĐrir de la vitesse à cause de l'ÃĐnergie potentielle de gravitation qu'il possÃĻde du fait d'Être ÃĐloignÃĐ de la terre.
Un autre systÃĻme oÃđ il y a transformation cyclique entre l'ÃĐnergie potentielle et l'ÃĐnergie cinÃĐtique est le mouvement d'un satellite
autour d'une planÃĻte, par exemple la lune et la terre. La solution de la mÃĐcanique classique dans ce cas montre que la trajectoire
du satellite est une ellipse, c'est à dire qu'il y a un moment oÃđ la lune est au plus ÃĐloignÃĐ de la terre
(ÃĐnergie potentielle maximum et ÃĐnergie cinÃĐtique minimum, apogÃĐe) et un autre moment oÃđ la lune est au plus proche de la terre
(ÃĐnergie potentielle minimum et ÃĐnergie cinÃĐtique maximum, pÃĐrigÃĐe).
Les systÃĻmes que nous venons de dÃĐcrire sont des systÃĻmes classiques mais ils ont leur correspondance dans le domaine quantique.
Par exemple le modÃĻle du pendule en mÃĐcanique quantique s'appelle l'oscillateur harmonique
et le modÃĻle du satellite correspond au modÃĻle de l'atome d'hydrogÃĻne: un ÃĐlectron satellite d'un proton.
En mÃĐcanique quantique l'ÃĐnergie cinÃĐtique est un opÃĐrateur faisant intervenir la masse, et l'ÃĐnergie potentielle
est bien sÃŧr aussi reprÃĐsentÃĐe par un opÃĐrateur dont la forme dÃĐpendra des ÃĐnergies en prÃĐsence: potentiel ÃĐlectrique, magnÃĐtique, ...
La façon dont la masse intervient dans l'ÃĐquation de Shroedinger, provient des travaux antÃĐrieur de Louis de Broglie
qui a ÃĐtabli la dualitÃĐ onde-corpuscule: Ã chaque particule de matiÃĻre on peut associer un onde dont la frÃĐquence
est proportionnelle à la masse. Ceci à partir des deux formules de l'ÃĐnergie:
E = m cÂē qui est la formule de l'ÃĐnergie de la relativitÃĐ restreinte d'Einstein : la masse est ÃĐquivalente à l'ÃĐnergie
E = h * nu qui est la relation de Planck-Einstein expliquant l'effet photo-ÃĐlectrique : l'ÃĐnergie est proportionelle à la frÃĐquence.
Il est important de comprendre que les ÃĐnergies en prÃĐsence exercent une contrainte sur le systÃĻme c'est à dire sur la
fonction d'onde. Lorsqu'on a affaire à des systÃĻmes oscillatoires comme l'oscillateur harmonique (pendule) ou l'atome d'hydrogÃĻne (le satellite),
la contrainte des ÃĐnergies a pour effet de localiser la fonction d'onde dans une rÃĐgion de l'espace.
Par exemple un systÃĻme classique soumis à aucune force (un mÃĐtÃĐore perdu dans l'espace inter-sidÃĐral oÃđ l'on peut nÃĐgliger
les forces gravitationnelles des ÃĐtoiles) se dÃĐplacera en ligne droite indÃĐfiniment.
L'ÃĐquivalent quantique est une onde plane qui se propage indÃĐfiniment, comme par exemple un photon qui n'est soumis à aucune force (les photons sont des particules sans masse ni charge ÃĐlectrique d'aucune sorte et ne sont donc soumis à aucune force ou ÃĐnergie).
Lorsque la fonction d'onde a une solution cyclique (fonction d'onde localisÃĐe) le temps n'a plus l'effet d'ÃĐloigner indÃĐfiniment
les parties du systÃĻme entre elles. L'ÃĐlectron restera localisÃĐ proche de son noyau qui est le proton dans le cas de l'atome d'hydrogÃĻne.
En mÊme temps si l'onde quantique se propage cycliquement dans une rÃĐgion finie, elle se recouvre elle-mÊme et donc elle interfÃĻre avec elle-mÊme
soit constructivement soit destructivement.
Dans la rÃĐsolution de l'ÃĐquation de Shroedinger de tels systÃĻmes, on voit que le temps n'intervient plus dans la forme de la fonction d'onde
et que c'est seulement l'espace (la position) qui dÃĐtermine la forme de l'onde. On est dans le cas des ondes stationnaires que l'on a dÃĐjÃ
ÃĐvoquÃĐ.
C'est à dire que les endroits oÃđ les interfÃĐrences sont constructrices, sont toujours les mÊmes ainsi que les endroits oÃđ elles sont destructrices.
L'onde stationnaire est un concept puissant qui permet de comprendre comment un phÃĐnomÃĻne statique peut provenir d'un phÃĐnomÃĻne dynamique.
C'est un des ÃĐlÃĐments qui permet d'intÃĐgrer la vision quantique: toute la stabilitÃĐ de la matiÃĻre dont nous faisons l'expÃĐrience provient
d'un enchevÊtrement d'ondes se dÃĐplaçant en permanence mais dont la rÃĐsultante par interfÃĐrence est stable.
Pour l'atome, ceci donne des orbites bien dÃĐfinies dont les formes sont fournies par les fonctions solutions de l'ÃĐquation de Shroedinger, les orbitales atomiques:
les nuages sont les nuages de probabilitÃĐs de prÃĐsence de l'ÃĐlectron. Plus le nuage est dense plus l'amplitude de probabilitÃĐ de prÃĐsence de l'ÃĐlectron est grande.
ReprÃĐsentation de l'amplitude de probabilitÃĐ des ondes stationnaires (harmoniques) de l'oscillateur harmonique. On notera la ressemblance avec
les ÃĐtats de vibration (noeuds et ventres de vibration) d'une corde vibrante.
On remarque que dans le cas quantique (Ã gauche) l'amplitude de probabilitÃĐ des fonctions d'ondes (en rouge) dÃĐcroÃŪt progressivement lorsqu'on
s'ÃĐloigne du centre c'est à dire dans les rÃĐgions oÃđ le potentiel devient plus fort (courbe parabolique en noir) mais n'est jamais totalement nulle.
Donc on a des chances lors d'une observation de trouver la particule dans une rÃĐgion ÃĐloignÃĐe oÃđ l'ÃĐnergie potentielle est plus fort que l'ÃĐnergie cinÃĐtique
alors que classiquement elle serait piÃĐgÃĐe dans la rÃĐgion oÃđ le potentiel est infÃĐrieur à son ÃĐnergie cinÃĐtique.
C'est ce fait qui est à l'origine de l'effet_tunnel qui permet à une particule quantique de traverser
une barriÃĻre de potentiel dont l'ÃĐnergie est supÃĐrieure à l'ÃĐnergie de la particule parce que la fonction d'onde n'est pas nulle de l'autre cÃītÃĐ
de la barriÃĻre permettant à la particule d'y Être observÃĐe. On retrouve ici une consÃĐquence de l'aspect non-local de la fonction d'onde.
C'est la contrainte que l'ÃĐnergie impose à la fonction d'onde de rester localisÃĐe et donc d'interfÃĐrer avec elle-mÊme pour produire des ondes stationnaires
associÃĐes à des valeurs particuliÃĻres de l'ÃĐnergie (valeurs quantifiÃĐes donc) qui est à l'origine du concept de "quantification".
Finalement il faut parler de ce qui est à l'origine mÊme de la thÃĐorie quantique: la constante_de_Planck
qui apparaÃŪt dans l'ÃĐquation de Shroedinger.
Cette constante a ÃĐtÃĐ introduite par le physicien Max_Planck pour expliquer la valeur du rayonnement thermique
de la matiÃĻre en fonction de la tempÃĐrature. La loi observÃĐe que suit ce rayonnement oblige à considÃĐrer que l'ÃĐnergie thermique n'est pas ÃĐmise
de maniÃĻre continue mais par paquet ou "quanta". C'est la premiÃĻre mise en ÃĐvidence du caractÃĻre quantique de la matiÃĻre.
En physique on dÃĐfinit l'action comme ÃĐtant le produit de l'ÃĐnergie par le temps. C'est assez intuitif: lorsqu'une ÃĐnergie agit pendant un
certain temps elle gÃĐnÃĻre une certaine action dont la valeur est proportionnelle à celle de l'ÃĐnergie et à la longueur du temps pendant
laquelle elle agit.
La constante de Planck reprÃĐsente la plus petite action possible dans le monde physique. C'est une constante universelle de la physique
qui caractÃĐrise la nature quantique de la rÃĐalitÃĐ.
La valeur de cette constante est extrÊmement petite: 6,62607004 à 10-34 m2 kg / s mais elle est nÃĐanmoins non-nulle.
0,000000000000000000000000000000000662607004
Lorsque l'on combine cette constante avec d'autres constantes fondamentales comme la vitesse de la lumiÃĻre ou la constante de gravitation universelle,
on dÃĐduit les quantitÃĐs minimales des diffÃĐrentes unitÃĐs de la physique : longueur de Planck, temps de Planck, etc... que l'on appelle les unitÃĐs de Planck.
Ainsi le monde physique tel que dÃĐcrit par la mÃĐcanique quantique possÃĻde une limite dans l'infiniment petit au delà de laquelle on ne peut plus parler
en terme de physique, c'est finalement un bord du monde physique.
S'il y a un bord, une limite, c'est une contrainte quantique naturelle pour la fonction d'onde donc pour la quantification (ce qui est en soi, on l'a vu, une force).
On peut aussi trouver l'origine la plus fondamentale de la quantification dans le fonctionnement de la conscience qui par nature n'est pas continue.
En effet si l'on considÃĻre l'observation par un sujet d'un objet qui est un point de vue dans la conscience, celui-ci n'est possible que par discrimination
de la conscience des diffÃĐrents points de vue possibles. Pour qu'ils soient identifiÃĐs les points de vue doivent Être distincts, sinon il y aurait fusion de tous les points
de vue et il n'y aurait pas vraiment d'observation. La discrimination est la qualitÃĐ de l'intellect qui est en ce sens une propriÃĐtÃĐ fondamentale de la conscience.
On retrouve ainsi les ÃĐlÃĐments prÃĐsents dans les postulats quantique de la mesure.
1.6.Expression poÃĐtique condensÃĐe des postulats
Ce qui suit est une tentative en un seul aphorisme de regrouper l'ensemble des postulats:
"Ce qui est possible s'accomplit, sous l'oeil de la conscience, seulement ce qui est possible s'accomplit."
La mÃĐcanique quantique est la plus grande rÃĐvolution de notre ÃĻre moderne scientifique car elle dÃĐtruit dÃĐfinitivement la position matÃĐrialiste,
ouvrant ainsi la voie à un dÃĐveloppement de l'humanitÃĐ oÃđ science et conscience seront à nouveau rÃĐunies.
La grande difficultÃĐ des scientifiques à accepter le message de la thÃĐorie quantique explique pourquoi si peu de personnes peuvent y avoir accÃĻs.
Ici vous trouverez un rÃĐsumÃĐ de cette situation, analysÃĐe par Jean Staune et reportÃĐ par Bruno Lussato:
bruno_lussato_les_plus_grandes_dÃĐsinformations_de_l_histoire_des_sciences
(blog oÃđ j'ai d'ailleurs laissÃĐ en 2009 un tÃĐmoignage sur la confÃĐrence qu'Alain Aspect a donnÃĐe en 1982 Ã Toulouse alors qu'il faisait le tour de France des universitÃĐs pour prÃĐsenter
le rÃĐsultat de ses travaux.)
Ce prÃĐsent texte aurait pu Être ÃĐcrit et probablement bien mieux par un grand nombre de personnes averties qui font partie de l' "establishment" scientifique
mais leur rÃĐpugnance à le faire m'a conduit d'une part à pouvoir rÃĐserver le nom de domaine quantique.org qui ÃĐtait curieusement disponible et d'autre part
à passer des dizaines d'heures à ÃĐlaborer ce texte.
L'expÃĐrience dÃĐcisive qui à permis de trancher le paradoxe
Einstein-Podolski-Rosen rÃĐalisÃĐ en 1982 par Alain Aspect chercheur et expÃĐrimentateur
au centre d'optique quantique d'Orsay ÃĐtait basÃĐe sur des photons.
Une description dÃĐtaillÃĐe de la thÃĐorie sous-jacente se trouve dans
le livre de Bernard d'Espagnat " A la recherche du rÃĐel" .
Cette mÊme annÃĐe, j'ÃĐtais à l'universitÃĐ et Alain Aspect est
venu prÃĐsenter ses rÃĐsultats à Toulouse, dans l'amphithÃĐÃĒtre Maxwell de l'UniversitÃĐ
Paul Sabatier.
L'Amphi ÃĐtait composÃĐ de trois travÃĐes sÃĐparÃĐes par deux escaliers. La
travÃĐe centrale, la plus importante ÃĐtait remplie de physiciens et d'autres
scientifiques de tout le campus de Rangueil. Sur les autres travÃĐes, il n'y avait personne ! C'ÃĐtait
trÃĻs curieux car ceux qui ÃĐtaient derriÃĻre au fond de la salle voyaient forcÃĐment
moins bien que s'ils s'ÃĐtaient rapprochÃĐs en venant sur les travÃĐes latÃĐrales. Cela
m'a amusÃĐ car je savais pourquoi il en ÃĐtait ainsi mais c'ÃĐtait quand
mÊme impressionnant. Ce qui allait leur Être annoncÃĐ serait comme un coup de massue sur la tÊte.
AprÃĻs avoir prÃĐsentÃĐ des rÃĐsultats de mesures sans ÃĐquivoque, il
a laissÃĐ l'assemblÃĐe sans voix (ou sans voie , l'amphi ÃĐtait rempli de professeurs et
de chercheurs) .
A la fin de la prÃĐsentation, aprÃĻs un instant de silence assez long,
significatif lorsque la parole à ÃĐtÃĐ donnÃĐ Ã une assemblÃĐe de scientifique, un
chercheur s'est levÃĐ (mon prof de relativitÃĐ Ã l'ÃĐpoque Alain Gautier) et à posÃĐ
cette question:
" Et vous trouvez que c'est facile de vivre avec cela maintenant ? " .
Aspect, sur la dÃĐfensive rÃĐpondit qu'il n'avait pas dit ça, qu'il avait fait
une expÃĐrience et que le rÃĐsultat ÃĐtait celui-là , mais qu'il se gardait d'y
donner une interprÃĐtation quelconque.
J'ai appris des annÃĐes plus tard par une personne l'ayant cÃītoyÃĐ qu'il
ÃĐtait pro-einsteinien et qu'il avait escomptÃĐ que la mÃĐcanique quantique
serait mise en dÃĐfaut.
J'ÃĐtais sur une travÃĐe latÃĐrale au troisiÃĻme rang, tout seul et j'ÃĐtais
amusÃĐ car je ne comprenais vraiment pas pourquoi cela leur posait un problÃĻme, oÃđ
plutÃīt je ne le comprenais que trop bien.
Lorsque l'expÃĐrience en ÃĐtait à ses prÃĐmisses mais que l'issue n'ÃĐtait
plus qu'une question de temps, la polÃĐmique est devenue trÃĻs forte, sulfureuse mÊme.
J'avais vu un article dans la revue de vulgarisation Science & Vie
qui prÃĐsentait une contre-expÃĐrience à celle d'Aspect menÃĐe par un physicien italien
qui disait que si l'expÃĐrience d'Aspect confirmerai la mÃĐcanique quantique alors
il arrÊterait la physique car cela n'aurait plus aucun sens pour lui. J'ignore s'il a
tenu parole.
Lorsque la communautÃĐ scientifique des physiciens ÃĐtait en ÃĐtat de choc,
on pouvait se demander ce qu'il allait se passer.
Il a fallu du temps pour que l'information soit digÃĐrÃĐe, on peut voir en
2020 que la situation à passablement ÃĐvoluÃĐ, il suffit de regarder
cette confÃĐrence donnÃĐe à l'ÃĐcole polytechnique par HervÃĐ Zwirn, directeur de
recherche au CNRS
_x_sciences_de_l_homme_et_de_la_sociÃĐtÃĐ_x_shs_mÃĐcanique_quantique_le_monde_existe_t_il
Cette expÃĐrience à eu (ou aurait dÃŧ avoir pour la majoritÃĐ) le mÊme genre
d'effet dans la communautÃĐ des physiciens que la dÃĐcouverte des
ondes hertziennes (ondes ÃĐlectromagnÃĐtiques) qui ont donnÃĐ au concept abstrait du
champ ÃĐlectromagnÃĐtique une rÃĐalitÃĐ beaucoup plus vivante. La dÃĐcouverte de la
non-sÃĐparabilitÃĐ et son observation au niveau physique donne vie au concept de la
rÃĐalitÃĐ indÃĐpendante, c'est à dire d'une rÃĐalitÃĐ indÃĐpendante de l'espace et du temps, c'est Ã
dire de toutes contingences spatio-temporelles, c'est à dire de
toutes contingences physiques.
Une premiÃĻre conclusion que l'on peut apporter au premier postulat de
la mÃĐcanique quantique est que:
La rÃĐalitÃĐ d'un systÃĻme quantique (et in fine, tout systÃĻme est quantique! )
est sous-tendu par un espace abstrait de possibilitÃĐs inobservable en soi (
non physique et indÃĐpendant de toutes contingences spatio-temporelles) mais
nÃĐanmoins rÃĐel, puisque c'est à partir de ce niveau de fonctionnement abstrait qu'ÃĐmerge
la rÃĐalitÃĐ concrÃĻte (observÃĐe) .
Pour rÃĐsumer cela en un mot: il s'agit d'omniprÃĐsence et d'omniscience
puisque cela contient toute l'information sur le systÃĻme physique de maniÃĻre
non-locale.
De plus, pour Être complet, cela est en lien avec l'observateur qui ne
peut ÃĐvidemment Être physique. Les postulats n'incluent bien ÃĐvidemment pas l'observateur
dans le systÃĻme physique mais dÃĐclare son existence nÃĐcessaire pour
qu'une observation ait lieu ou qu'un rÃĐsultat physique soit produit.
L'ÃĐvidence apparaÃŪt alors que l'observateur et la
rÃĐalitÃĐ indÃĐpendante entretiennent un rapport ÃĐtroit: ils sont tous deux non physiques
et interagissent en termes d'information, de connaissance, de perception. Cela
rejoint parfaitement les conceptions du "rÊve du monde" des shamans.
Le film Matrix peut Être à ce sujet, considÃĐrÃĐ comme une allÃĐgorie de
la rÃĐalitÃĐ quantique. La diffÃĐrence avec la rÃĐalitÃĐ est que la
simulation holographique du monde n'est pas fabriquÃĐ par des ordinateurs matÃĐriels mais par
un ordinateur cosmique non matÃĐriel qui s'identifie à la conscience dans sa
conception la plus ÃĐtendue.
On peut donner et on a donnÃĐ Ã cette conscience universelle tous les
noms que l'on veut mais ceux-ci n'ÃĐpuiseront jamais la puissance infinie de
cette Conscience.
On parle alors d'ÃĐtat ÃĐquiprobable.
Dans notre cas on a donc:
Si on applique cet opÃĐrateur au ket | Psy > on a :
Mais si on n'observe pas cette propriÃĐtÃĐ du systÃĻme alors le systÃĻme reste dans cet ÃĐtat de superposition
des fonctions d'ondes boulanger. On dit que l'ÃĐtat est dÃĐgÃĐnÃĐrÃĐ.
Dans ce cinquiÃĻme postulat nous avons vu que la mesure elle-mÊme transformait le systÃĻme.
ConformÃĐment au cinquiÃĻme postulat, lors d'une mesure la fonction d'onde collapse vers un sous-espace propre de maniÃĻre instantanÃĐe affectant
en mÊme temps l'ÃĐtat de toutes les particules composant le systÃĻme.
Cette expÃĐrimentation a prouvÃĐ de maniÃĻre indiscutable que la fonction d'onde ne dÃĐpendait pas de l'espace physique dans lequel nous vivons:
son ÃĐvolution lors du collapse dÃŧ à l'observation s'effectue en tout point de l'espace en mÊme temps.
L'expÃĐrience d'Aspect a ÃĐtÃĐ maintes fois reproduite dans des conditions de plus en plus sophistiquÃĐs pour pousser la mÃĐcanique
quantique dans ses retranchements mais celle-ci n'a jamais cÃĐdÃĐ !
Dans une telle thÃĐorie la fonction d'onde serait | Psy > et non plus | Psy(t) > .
Le temps serait une observable T au mÊme titre que la position P.
La particularitÃĐ de cette expÃĐrience de pensÃĐe complÃĻtement irrÃĐalisable telle que prÃĐsentÃĐe avec un "vrai chat" est de
faire rÃĐflÃĐchir à ce qu'est l'observateur en mÃĐcanique quantique.
| dÃĐtecteur, particule > = | ÃĐtat particule dÃĐtectÃĐe > ÂĪ | particule prÃĐsente >
+ | ÃĐtat particule non-dÃĐtectÃĐe > ÂĪ | particule absente >
+ | ÃĐtat particule non-dÃĐtectÃĐe > ÂĪ | particule prÃĐsente >
+ | ÃĐtat particule dÃĐtectÃĐe > ÂĪ | particule absente >
Si rien de matÃĐriel n'opÃĻre la mesure, il ne reste plus que quelque chose d'immatÃĐriel qui le fait et cela Wigner l'identifie
à la conscience qui identifie finalement ce qu'est l'observateur.
bernard_d_espagnat_physique_quantique_et_rÃĐalitÃĐ_la_rÃĐalitÃĐ_c_est_quoi ;https://www.youtube.com/watch?v=Jd8FiWJ5v8M;
Cette Maya ÃĐtant fabriquÃĐe par les inter-relations infinies entre trois ÃĐlÃĐments : richi, chandas et devatta qui sont le sujet, l'objet et leur
mise en relation, la connaissance (spirituelle: de l'esprit) ou la perception (matÃĐrielle: de la matiÃĻre).
Les triades suivantes sont ÃĐquivalentes:
veda philosophie physique quantique
rishi sujet observateur connaisseur observateur
devatta perception (relation sujet/objet) observation connaissance observable chandas objet observÃĐ connu rÃĐsultat de la mesure: valeur propre de l'observable
Cette position dit qu'entre deux mesures il n'y a pas d'objet et que le seul objet qui existe est "l'objet observÃĐ".
Le terme classique correspond à ce que l'humanitÃĐ perçoit dans son ensemble de la mÊme façon. Mais cette position rentre en conflit avec
la rÃĐalitÃĐ quantique qui est donc perçue comme totalement paradoxale.
C'est à dire que lorsque le systÃĻme a dÃĐcohÃĐrÃĐ, il est descriptible classiquement car l'aspect quantique
s'est ÃĐvanoui.
Lorsque la fonction d'onde d'un ensemble de particules "dÃĐcohÃĻre" dans le collapse de la mesure
l'aspect ondulatoire de la mÃĐcanique quantique disparaÃŪt et il ne reste plus que l'aspect corpusculaire.
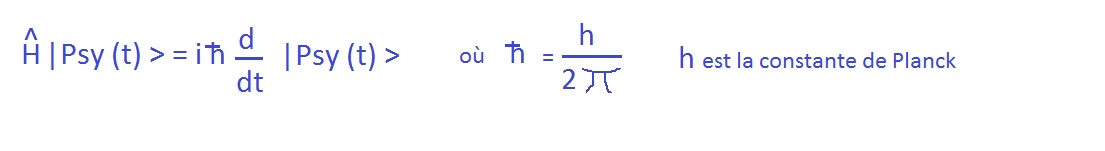
Il est clair que c'est l'ÃĐnergie qui fait ÃĐvoluer les choses. L'ÃĐnergie et le temps sont des grandeurs intrinsÃĻquement liÃĐes.
On dit qu'elles forment un couple de variables conjuguÃĐes.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf
Plus le temps passe plus l'ÃĐnergie potentielle se transforme en ÃĐnergie cinÃĐtique et lorsque le caillou arrive au sol, il casse la vitre
en vertu de l'ÃĐnergie cinÃĐtique qu'il aura acquis au dÃĐtriment de son ÃĐnergie potentielle qu'il aura perdu. Si on le pousse dans un puits
il continuera le mÊme processus jusqu'à ÃĐpuiser totalement son ÃĐnergie potentielle si c'est possible.
Si on considÃĻre le mouvement d'un pendule (un caillou accrochÃĐ Ã un support par une ficelle) celui-ci oscille, c'est à dire qu'à partir
de la position de dÃĐpart (à un certain angle de la verticale) oÃđ le caillou est lÃĒchÃĐ, celui-ci va accÃĐlÃĐrer jusqu'à ce que la ficelle soit à la verticale, puis va ralentir
jusqu'à s'arrÊter de l'autre cÃītÃĐ dans une position symÃĐtrique par rapport à la position de dÃĐpart et à la verticale.
Le pendule transforme son ÃĐnergie potentielle en ÃĐnergie cinÃĐtique puis son ÃĐnergie cinÃĐtique en ÃĐnergie potentielle et cela cycliquement.
Si le systÃĻme ne subit aucune autre force le mouvement ne s'arrÊte pas. En pratique il y a toujours des forces de frottement qui dissipent
l'ÃĐnergie en chaleur jusqu'Ã ÃĐpuisement. Mais ce dernier point n'est vrai qu'en mÃĐcanique classique parce qu'en mÃĐcanique quantique
il n'y a pas de frottement !
Ainsi on voit que dans l'ÃĐquation de Shroedinger est intÃĐgrÃĐ un rÃĐsultat de la relativitÃĐ restreinte d'Einstein.

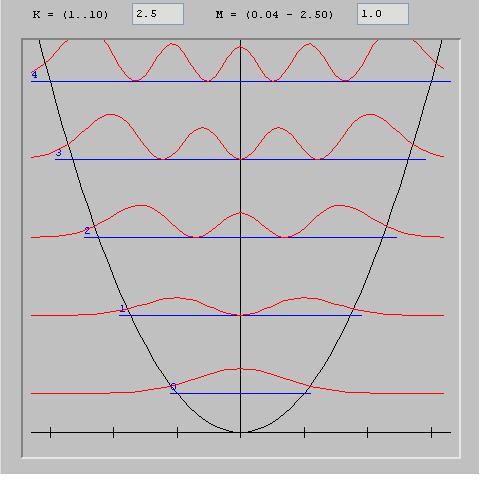
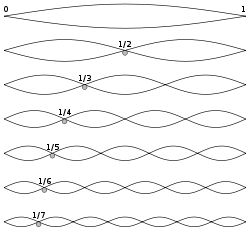
La constante de Planck dÃĐfinit la pixellisation de l'Univers. cf structure du vide quantique
poÃĻme correspondance quantique lien vers les postulats
Ce qui est la fonction d'onde ou vecteur d'ÃĐtat ou "ket" (de bracket , crochet en français) Premier postulat
possible la structure probabiliste de la fonction d'onde, les diffÃĐrentes possibilitÃĐs ÃĐtats propres du ket TroisiÃĻme postulat s'accomplit la dynamique de l'Hamiltonien opÃĐrateur ÃĐnergie totale du systÃĻme responsable de l'ÃĐvolution. DeuxiÃĻme postulat sous l'oeil de la conscience les postulats de la mesure c'est à dire l'intervention nÃĐcessaire de l'observateur QuatriÃĻme postulat seulement ce qui est possible s'accomplit seules les valeurs propres de l'observable peuvent Être obtenues et l'ÃĐtat du systÃĻme est alors l'ÃĐtat propre correspondant. CinquiÃĻme postulat Ce qui est possible s'accomplit l'ÃĐquation de SchrÃķdinger, l'ÃĐquation de la dynamique quantique. SixiÃĻme postulat