Document . les postulats de la mecanique quantique
version available in : en it ru es ja de nl pt fr
date of creation : 20240129- date of update : 20221007- generation date : 20241110_231431
这篇文章详细介绍了 postulats_de_la_mécanique_quantique从简单的数学和几何考虑以及日常生活中的类比中得出的结论.
在物理学中,与数学对象有关的概念被开发出来,以建立理论,使物理世界能够通过其运行规律得到体现.
经典力学或牛顿理论是允许我们在对人类感知敏感的尺度上表示物质的运作的理论,我们称之为宏观的.
在宇宙学尺度上,这一理论通过爱因斯坦的相对论得到了概括。.
广义相对论是最全面处理引力问题的理论.
量子力学是允许我们在微观层面上表示物质的运作的理论,尽管微观和宏观之间的界限在尺度上没有明确的定义,因此我们可以在宏观尺度上有量子行为,如在 laser或 cables_électriques_supraconducteurs 量子理论并不像广义相对论那样处理自然界的一种特定力量,它更像是一种语言.
量子对象的语言.
因此,我们可以将这种语言应用于各种力量或系统,从而将其量化.
这套量子概念围绕着 全面定义量子理论的六个基本假设.nweb超导电力电缆 我们将介绍这六个假设,并试图以一种简单的方式确定它们的含义.
科恩-塔努吉的书"量子力学第一卷"中定义的第一公设的表达方式是 :
在一个固定的时间t,一个物理系统的状态是由数据定义的
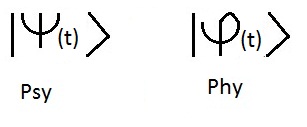
的凯特或波函数或状态矢量指出 |幻想(t)>属于状态空间的"。.
岗位设置 I nweb
希腊字母Psy被用来指定波函数,我们用
也漠不关心的信Phy.

力学的第一个概念涉及到物理系统状态的表述.
这是对研究对象进行定义的一种自然方式.在这里,我们简单地说,该系统存在
并且其状态可以用一个随时间变化的函数来表示
这是因为系统的状态不是先验的静态,而是动态的。.
在经典力学中,物理系统是由"物质点"代表的.
一个复杂的系统将由一组连接的材料点来表示
它们之间形成一个固体或非固体物体 (刚性或非刚性连接,例如:晶体或气体).
第一个公设简单地指出,系统在某一特定时间的状态是唯一的
并属于一个可能的状态集合,该集合被归为
数学上称为"状态空间".
我们说的是空间而不是简单的集合,因为量子态是一个矢量
这是一个数学对象,表示空间中的一个方向.
我们都知道三维空间 (长、宽、高或深,取决于前两个维度的方向)
它是我们生活的物理空间.
量子系统"生存"的状态空间不是一个物理空间,是一个抽象的空间 (希尔伯特空间)
它的维度是无限的,以代表即使是简单的物理系统也存在的无限的可能状态.
让我们用日常生活中的一个例子来做个比喻吧
了解量子系统是如何被建模的.
想象一下,一个人安静地坐在自己的公寓里,突然间
意识到她必须要出去买面包了.
她准备离开,在她的脑海中,她仍然对这个地方犹豫不决。 她去买面包的地方.
她可以选择街边的一家面包店,或者是一家也做面包的糕点店。
与她同在一条街上的人.
下楼出口,可以说有两种状态 在他的脑海中,有两种可能,分别对应于以下两个选项 买面包.这些选项可以以量子化的方式注意到:
状态1: |面包师>
状态2: |糕点店>
这个人的心理状态是这两种可能性的组合:
|状况> = |面包师> + |糕点店>
这两种状态是完全不相容的:或者她买了面包 在面包师那里,或在糖果师那里.这两种可能性都有 没有共同点,他们没有共同点.几何学上 它们将被称为是正交的 (垂直)和空间的几何表现 (的国家,所以)将是:
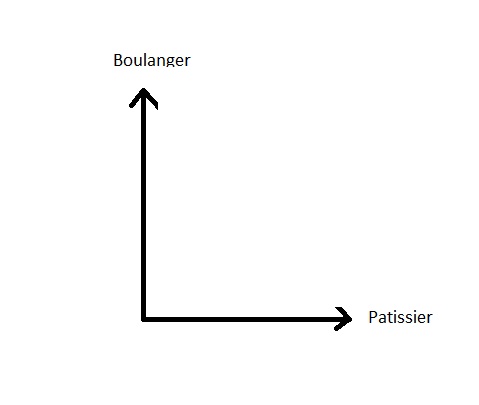
因此,我们有两个非常不同的方向,它们没有任何共同之处.
如果箭头 (向量)贝克向箭头倾斜 (向量)糕点店
那么这就意味着,要从
面包师与去买东西有点联系
在糕点店,情况并非如此,它们是两个
不兼容的选项:正交,即成直角:他们在领导方面没有任何共同点.
另一方面,系统的状态,即思想的状态
的人是两个状态的所谓线性组合.
我们说,我们有一个混合的状态.真正的混合状态并不是
并不对应于任何可观察到的东西:我们不知道
不是买面包的地方.
这两种可能性的线性组合对应的是
为代表可观察状态的两个向量之和.
两个向量之和的实现方式如下 :我们做
从第一个向量和第二个向量的末端来看
从第一项的开始到结束的总和
的第二个.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
据说状态空间是一个矢量空间,即一个方向的空间。 这意味着在几何表示法中,我们可以移动矢量而不改变它们 自然,它们仍然是相同的矢量:它们指向同一个方向.也是为了简化 表示,所有的向量都从同一点开始,以表明只有 在这个空间存在的方向.这被称为矢量空间,与之相对的是 到一个点的空间,这在数学上被称为仿生空间. (的屏幕上。 你正在阅读的这篇文字是一个仿生空间的例子,像素代表该空间中的点。.状态总和向量 img)
几何表示显然是在一个点的空间中完成的,因为一个矢量空间
是一个纯粹的抽象概念,只能用点来表示我们所感知的空间。 (职位)不同的.
但这并不存在于状态空间中,在那里,一个向量在不同时间的所有表现都是
表示空间中的位置对应于矢量空间中的一个矢量.
因此,状态可以表示如下 :
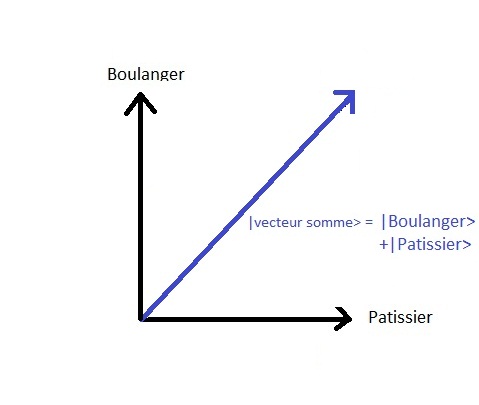
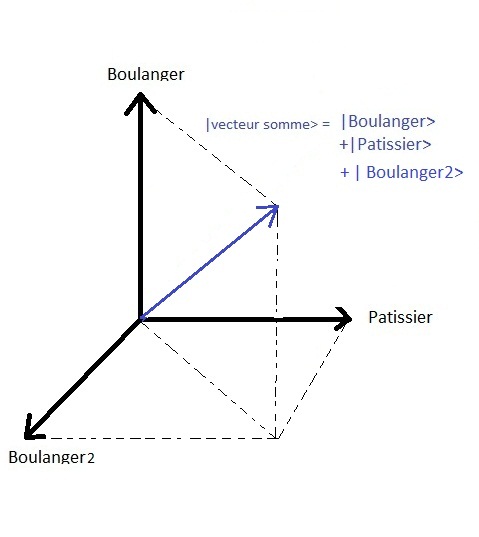
这里状态空间的维度为2.如果有第三种选择
与相邻街道的另一个面包师 |烘焙师2 >那么状态空间将是三维的,等等。.
在物理学中,双态系统可以用同样的方式来建模.
这就是电离氢分子的情况.氢气分子
是由两个氢核组成,即两个质子
而它被电离的事实意味着一个电子已经从它身上被移除。
它自然而然地拥有了这两者中的一个.比如说
因为它是简单的 :***到一个电子***.
电子的两种可能的位置状态是 : - 要么电子以原子核为中心 1 - 要么电子以原子核为中心 2
几何表示法是:
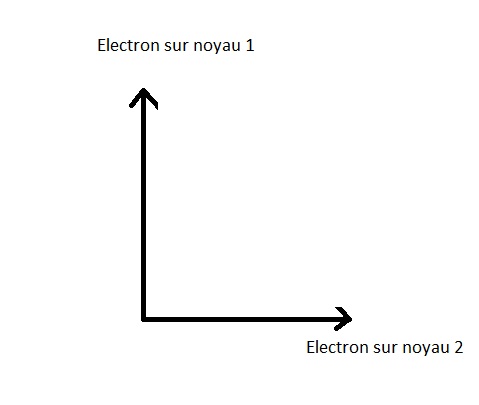
很明显,电子不能被发现 (或者说是被发现,即 :被观察)在核心1和核心2上同时出现,这些状态是正交的。.
在定理的表达中,同义词被用来指定状态矢量,它被称为无所谓地
状态向量、波函数或酮体.这些不同的名称对应于状态向量的不同数学方面.
我们将在第二个公设的解释中看到波函数方面,在第三个公设中看到"ket"方面。.
综上所述,量子态由给定的向量表示 (方向)在一个向量空间中 (的方向),
这个向量被称为"状态向量"。.
在经典力学中,状态是由"物质点"表示的,它是由其物理特性定义的 位置和速度.
需要注意的是,在量子力学中,系统的状态是完全独立于系统的状态的。
系统的物理特性.状态的定义是抽象的,可以说是"非物理的"。.
这将在通过"状态矢量表征基础"的概念介绍以下公设时详细说明.
但可以注意到,第一个公设使状态矢量只取决于时间而不取决于位置
这就是空间.这意味着波函数是非局部的.
显然,相对论告诉我们,时间和空间形成了一个连续体,因此,如果一个表述的
量子力学至少考虑到了狭义相对论,状态矢量不取决于
的时间.这个理论就是量子电动力学或电磁场的量子理论.
狭义相对论与电磁学有很大关系,因为爱因斯坦提出了这一理论
以消除麦克斯韦的电磁理论所带来的悖论.
量子概念不是由纯粹的想象力来构思的.相反,它们是在实验的火焰中被锻造出来的。
微观物理学,需要这些概念的正确表达.
虽然完全抽象,但量子态是真实的.
正是这种量子状态的现实,往往仍然是最难承认的,即使它是不可避免的.
物质的运作,也就是最具体的东西,是由完全抽象的东西支配的。.
然而,要绕过这个困难是不可能的,因为这个量子概念是特别牢固的.
认知情况有点类似于电磁波的发现.这些波首次在理论上被
通过结合麦克斯韦描述电场和磁场的方程发现的.
他们的组合提供了一个具有恒定速度的波传播方程.这是一个抽象的概念
和新的,但实验表明,电场和磁场确实产生波
可以控制和使用,这导致了无线电通信的出现.
我们已经看到,这个速度是测量的光速.
同样地,非常抽象的波函数概念在以下方面变得非常具体了intrication_quantique 并催生出了 \"技术领域\"。 cryptographie_quantique
第二条公设
.
Postulat_II
"任何可观察的物理量'a'都是由作用于状态空间的算子'A'描述的;这个操作者是一个可观察的.
" 在经典力学中,我们已经看到,决定其状态的是材料点的属性、其速度和位置.
例如,网球场上的球或太阳系中的行星的速度和位置.
宏观物体的位置和速度在每个瞬间都是确定的,这完全定义了系统的状态.
网球在空间中的演变在每一时刻都决定了比赛的状态,如果球在运动中,"出"或不在运动中,或在接网后在地面上不动。.
而正是其国家的历史决定了比赛和结果。.
另一方面,在量子力学中,还原为粒子的系统的一般状态,如前面例子中的电子,不再与一个特定的位置或速度相关,而是与所有可能的位置或速度的混合物相关。.
此外,我们不能像经典力学那样同时观察系统的所有属性.
如果系统处于位置状态,它就不处于能量状态,反之亦然。.
在面包的例子中,我们有位置状态,即面包师和糖果师,它们表明面包的购买地点,但正如我们将看到的,这些不是能量状态。.
正如在氢分子的例子中,电子位于核1或核2的事实代表了位置状态,但这些本身并不是分子的能量状态。.
在一个量子系统中,不同的属性共享相同的状态空间,但对应于不同属性的状态不一定由空间中的相同方向来表示.
这意味着,如果空间是二维的,那么将有两种可能的位置状态,但也有两种可能的能量状态,而且能量状态的方向与位置状态不一样。.
在氢分子的情况下 (电离)可能的能量状态是:
|状况:能源> = |相关国家> |非约束状态>
在氢分子的"动态或能量"表示中.
系统的一般状态完全独立于其属性,因此对于面包,我们可以写成:
|状况> = |确定> |放弃> = |面包师> |面包师>
对于氢分子调用El (相关国家)和Enl (非约束状态)是能量状态,P1和P2是位置状态,我们有:
|状况> = |ǞǞǞ > |启迪 > = |P1 > |P2 >
状态独立于其可观察的属性,并且可以不受这些属性的影响来表达,这是量子力学的一个基本特征.
这些属性由数学算子表示,当应用于量子态时,确定该属性的可能状态.
数学中的运算符是使广义上的数值演变的东西.
例如,对于加法,运算符"3 "应用于"2",得到"3 2"。="5"我们通过应用运算符"3",将数值从"2"改为"5"。 (加值三) 在量子力学中,算子使状态发生演变.
该公设说,算子"作用于"状态空间.
设P为位置算子,E为能量算子 (在现实中,能量算子被表示为H,用于 hamiltonien_zh这是汉密尔顿在一般力学中定义的总能量函数,即作用于系统的所有能量的总和).
根据第二个公设,这些运算符代表相应的属性 (位置和能量)的系统.
通过应用 (使其发挥作用)氢分子状态上的位置算子,我们有:
P |身份 > = |P1 >或P |身份 > = |P2 >.
在状态上应用算子意味着观察与算子相对应的属性,这里是指位置.
以同样的方式与能量算子.
H |身份 > = |ǞǞǞ > 或H |身份 > = |启迪 >.
我们可以看到,当我们对一个状态应用一个运算符时,我们使这个状态向属于这个特定运算符的状态演变,我们称这个状态为 "干净的状态"的操作者.
其结果可以是系统和操作者的任何可能状态 (被测财产).
国家 粘合的分子"^。是能量算子的一个特征态,而 *核心的电子1***。是算子位置的一个特征状态.
对于处于结合态的氢分子来说,电子在两个氢核之间的位置是不确定的.
能量特征态可以说是位置态的线性组合,可以表示为:
|ǞǞǞ > = |P1 > |P2 >
这两个位置状态可以说加起来是一个能量状态:当电子被两个核共享时,分子就被束缚住了,这两个位置态被说成是建设性地相互影响,形成"束缚"的能量状态。.
以同样的方式,未绑定的状态将被表示为 |启迪 > = |P1 >- |P2 >
据说,这两个位置状态会发生破坏性的干涉,从而产生能量状态"无束缚"。.
如果我们再拿面包来比喻,这个人的心理状态是在去买面包师或糕点师的面包之间犹豫不决,但也在去买面包或不买面包之间犹豫不决。.
可以说,出去买面包的决心是一种 interférence_zh的所有可能性去买面包,而放弃是一种 interférence_zh破坏性的这些相同的可能状态.
我们考虑可能发生在系统上的所有可能性,这些可能性都包含在状态空间中。.
从几何学上看,这可以表示为以下几点:
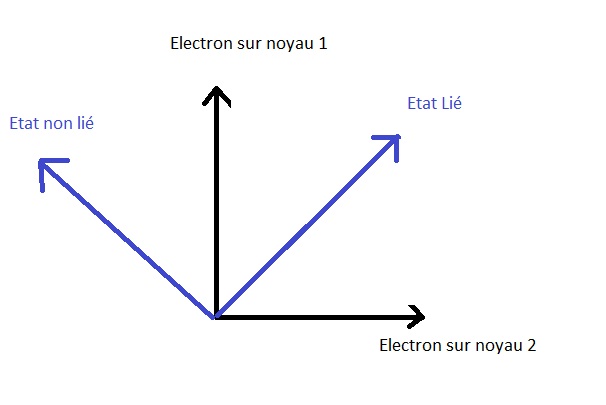
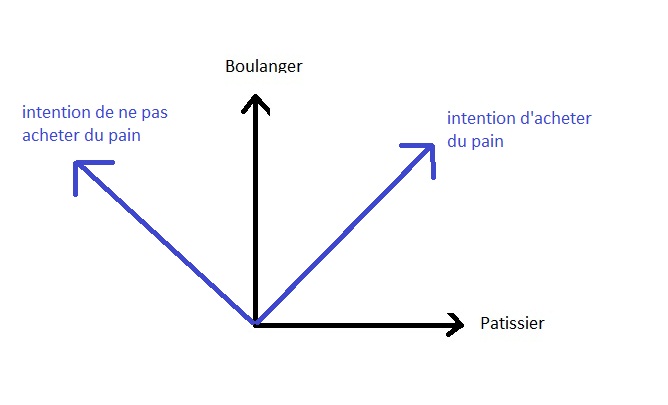 可以看出,可观察到的能量状态是 (分子的结合或未结合状态)也是正交的,因为它们对应的是相互不兼容的可能的能源选择.
可以看出,可观察到的能量状态是 (分子的结合或未结合状态)也是正交的,因为它们对应的是相互不兼容的可能的能源选择.
系统的状态 (状态向量)本身独立于它在状态空间的表示,无论是能量还是位置.
与一个算子相关的特征状态被说成是代表状态向量的基础 (这里的蓝色或黑色底座) 因此,对于状态向量,我们有一个位置算子的表示基础和一个能量算子的不同表示基础.
ǞǞǞ principe_d_incertitude_de_Heisenberg直接来自于量子力学的定理.
我们已经看到,一般来说,两个观测变量的特征状态并不由相同的向量来表示,例如,一个能量状态将由一个线性组合来表示 (叠加)的位置状态.
在这种情况下,很明显,在同一个测量过程中,不可能同时观察到一个系统的位置属性和能量属性,因为它们的特征状态是不相容的。.
在数学上,我们说,运算符不切换.
这意味着,如果两个运算符以不同的顺序连续应用于系统,那么最终状态将是不同的。.
实际上,在量子实验中,大量的粒子被观察到,这就给出了一个全局性的统计结果,其中似乎能量值越精确,位置越不精确,反之亦然。.
状态向量和波函数的区别在于,状态向量与物理空间无关,而波函数则不然,因为它在物理空间中传播。.
在量子力学中,波函数被说成是状态向量在物理空间中的投影.
在下面的图片中,我们已经表示了波浪的方面 (波函数)的量子态
想象出波是如何通过加减法进行破坏性或建设性的干扰的.
波的基本功能是相同的,无论它是一个量子波、一个
电磁波或例如水体表面的波浪 (隐约可见).
一个波浪总是有一个波谷和波峰的震荡 (的波浪)围绕着一个平均数值 (水面).
优点加起来 (以及最少的)而且正负相减,相互抵消。.
例如,如果一个波谷与另一个波的波峰相遇,两者相互抵消,留下
重叠点处的平坦水面.
原子或分子的波态对应于 ondes_stationnaires_zh
这是不传播的波,但主要是在有限的区域内保持局部。
的空间,这里围绕着氢核.

因此,第二个公设介绍了应用于状态的运算符,以转换它们.
因此我们可以说,状态矢量代表了量子现实的静态方面,而算子代表了这一现实的动态方面.
第三、第四和第五条公设描述了观察量子系统的过程本身.
第三个假设
.
Postulat_III
衡量标准 :观察物的可能值 "对一个物理量A的测量只能给出所有可能的观察物A的一个特征值.
" 我们已经看到,量子系统的一个属性的可观察状态被称为"特征态"。 (这个可观察到的).
每个"特征态"都有一个相关的"特征值",这是测量的结果.
例如,对于氢分子来说,如果分子处于结合态或非结合态,它将是分子的能级不同。.
在面包的比喻中,人们可以想象,结果是购买面包时钱包里的钱数减少的变化.
特征值是一个数字,而特征状态是,正如我们所看到的,一个矢量.
到目前为止,我们只使用了矢量的方向,它也与状态空间的一个维度相关,因为这是关于量子状态的最重要的概念.
在数学中,与一个矢量相关的自然值是它的长度.
这个长度是抽象的 (它不是物理空间,所以不能用米来衡量).
由于这个原因,一个指长度或尺度的更普遍的术语被创造出来,因此被称为"标度值"。.
因此,标量是与矢量的长度相关的数值.
如果我们把一个向量的长度乘以一个数字,我们将得到一个长度是初始值的倍数的向量,它将处于不同的尺度上,它的新值"scalar"。.
因此,我们在这里使用能量算子观察系统的能量.
我们已经看到,在这种情况下,对状态的能量算子的应用同时给出了两种可能的能量状态:
H适用于 |身份 >将给国家 |ǞǞǞ > (链接)与能量El相关的状态是 |启迪 > (为不相关的)与能源相关的 Enl (能量是能量算子的特征值).
逻辑运算符"或" (或非排他性)在量子力学的状态空间中,由注意到的向量的加法来表示""。.
因此,我们有:
H |身份 > =ǞǞǞ |ǞǞǞ > 启迪 |启迪 >
全局状态是可能的特征状态的叠加,其中El和Enl分别代表两个状态的能量值,正如我们已经看到的那样.
为了表示在测量过程中只可能有一个值的事实,我们使用矢量的一个属性,称为投影.
以下是全球状态投影的图像 |诗意>关于能量状态"结合分子"的问题 |ǞǞǞ >
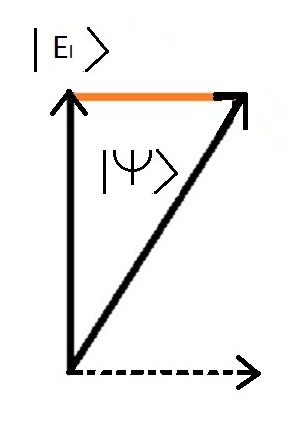 当对系统的物理性质进行测量时,假定测量给出一个唯一的值,这个值对应于系统的一个特定状态,称为"特征状态",得到的值被称为"特征值"。.
当对系统的物理性质进行测量时,假定测量给出一个唯一的值,这个值对应于系统的一个特定状态,称为"特征状态",得到的值被称为"特征值"。.
在前面的等式中,我们增加了可能性而不是数值,所以我们没有E =El Enl,添加一个向量的工作方式不像添加一个值那样。 (标量).
我们稍后将看到,增加可能性不会导致能量的总和,而是导致能量的平均值,即数值的总和 (El Enl)除以增加的值的数量 (ii 2).
因此,平均能量值将是E = (El Enl)/2.
在现实中,它比这更微妙,因为能量的平均值也取决于每个能量状态存在的概率,所以它是一个由每个状态的概率加权的平均值.
这正是第四条公设的主题.
Postulat_IV
出生公设 :波函数的概率解释 "当在归一化状态"phi"的系统上测量物理量A时,其概率P (一个)以获得相应的可观测变量A的特征值An,即为 |Cn|².
其中Cn是波函数投影到特征态上的振幅 |phi n>对应于观察到的特征值An.
到目前为止,我们只谈到了状态、可观测的特征态及其相关的特征值.
按照惯例,任何状态向量的长度都是1,原因是状态向量传达了系统的存在。 (第一个假设)而就概率而言,对该系统存在的肯定对应于一种确定性.
在概率中,确定性是1.
当你有1/1的机会时,任何事情都有可能发生 (1除以1等于1)我们是在肯定的.
小于1的概率比完全确定的概率更不确定.
例如,只玩一个格子就能赢得彩票的机会是1除以几百万。.
这意味着,最终只有一个人或几乎一个人将在抽奖中赢得百万奖金。 ! 在量子方面的平局是"对赢家的观察"。.
波函数的振幅与状态矢量的长度相同.
我们已经看到,一个标量是一个简单的数字值.
这一称呼也出现在与由几个数字组成的更复杂的数值的比较中,如向量,当用数字表示时,需要使用几个数字。.
(如果我们沿着这条路线发展,我们就会得出物理学中非常常用的"张量"的概念,弹性的张量,时空的曲率的张量...推测四 nweb).
_
当一个向量投射到另一个向量时,从第一个向量到第二个向量所携带的长度是一个数字.
因此,我们已经进行了一个操作,将一个数字与两个向量联系起来,我们称之为标量,以表明两个向量的这种操作的特定结果并不像向量相加那样给出第三个向量,而是一个数字。 (标量).
这种操作被称为标量乘积: 标量积是一种运算,从两个向量中可以得到一个数字.
这个数字是一个矢量在另一个矢量上的正交投影长度。.
英文单词"bracket"指的是字符"。<" et ">" 这些括号在数学中传统上用来表示一个数量的平均值.
能源的平均值将被注意到,例如 < E >.
我们已经看到,量子态也被称为"ket"注意到了 |ket > 括号的另一部分是"bra",它是一个特殊的运算符,请注意 <文胸 | 它是物理学家 Paul_Dirac这是这个词一分为二的起源,以便在取平均值的操作中出现运算符和矢量的动态。.
如果我们将"bra"应用于"ket",我们可以得到 <文胸 |ket >这是由应用运算符产生的数字 <文胸|关于国家 |ket>或国家的预测 |文胸>关于国家 |ket>.
在这里,我们有一个胸罩和ket之间的双重关系.
对于一个国家来说 (ou ket)"|犬类 ><犬类 |" 两者之间的二元性被表示为镜子中的图像 Ket是一个矢量,而Bra是一个算子,将Bra应用于Ket,得到一个数字.
一般来说,在一个表达式中,ket右边的东西是一个运算符,一个运算符对一个状态的结果 (向量)是另一个国家 (向量)一个代表测量结果的数字或一个概率.
每一个ket都有一个相应的bra,允许从ket到bra的操作被称为hermitic conjugation,并以星号表示。.
因此 ( |犬类 > ) = <犬类 |或 ( <犬类 | ) = |犬类 > 或 |文胸> = (ket>Paul Dirac nweb) <经营者| = (身份>Paul Dirac nweb)*因此,胸罩是动态的方面 (经营者)杜凯特 (身份)产生表现的 (测量结果 ).
这可以类比于《吠陀经》中的一句箴言,宇宙的创造者说: "在自己身上转来转去,我一次又一次地创造"。.
同样的形式也可以在《创世纪》的第一个创造故事中看到: 就有了光,就有了光,就有了D.
上帝看到光是好的.
<让我们有光 |而光是 > =和D.
上帝看到光是好的.
<或 |光²。 |木桶 > =D.
上帝看到光是好的.
事实上,D.
上帝看到光是好的,这显然是一个观察的结果.
我们可以把这一切称为量子的字母和语法.
字母表只由一个字母组成 |犬类 >而这是"的存在"。 (或者说是对存在的肯定的状态) 双重操作*显示其动态操作值 ( |犬类 > ) = <犬类 | 它们的所有组合产生了量子语法.
一个例子是操作者的应用 <犬类 |关于国家 |犬类 >给予 <诗意|犬类 >的投影,这也是 |诗意>在自身上,因此是1.
这可以微妙地转化为以下句子:"Psy 100%参与。 (100/100=1)to Psy".
<犬类 L |犬类 >是系统的一般状态对H2分子的约束能量状态的投影,表示在观察期间获得约束状态的概率振幅。.
ǞǞǞ = <犬类 L |犬类 > 取振幅的平方得出概率 状态的概率 |犬类 L >是:プラス =Al² = ( <犬类 L |犬类 > )² 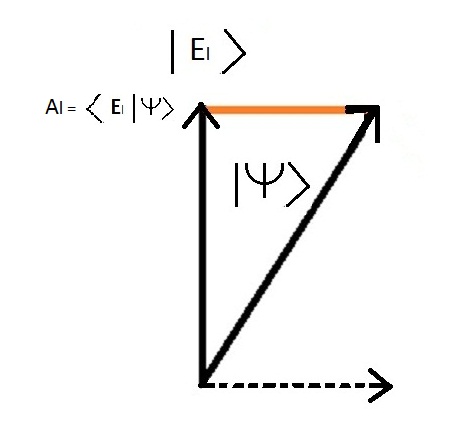
下面的图片代表了一般状态的投影 |犬类 >在两个能量状态上 |犬类 l >和 |狗狗 nl > (这是与国家相同的 |ǞǞǞ >和 |启迪 >这只是符号上的差异)
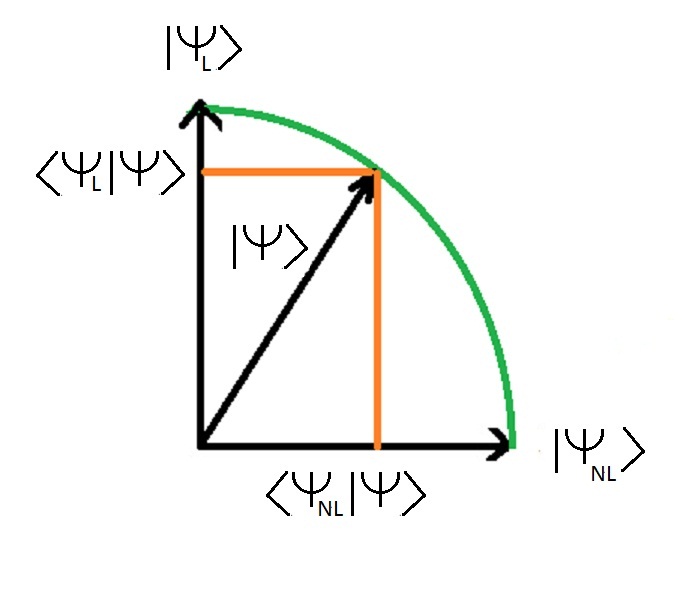 这两个值 <犬类 l |犬类 >和 <狗狗 nl |犬类 >是状态的长度 |犬类 > (这是个1)对自身报表的预测 |犬类 l >和 |狗狗 nl > <犬类 l |犬类 >是状态的投射 |犬类 >关于清洁状态 |犬类 l > <狗狗 nl |犬类 >是状态的投射 |犬类 >关于清洁状态 |狗狗 nl >
这两个值 <犬类 l |犬类 >和 <狗狗 nl |犬类 >是状态的长度 |犬类 > (这是个1)对自身报表的预测 |犬类 l >和 |狗狗 nl > <犬类 l |犬类 >是状态的投射 |犬类 >关于清洁状态 |犬类 l > <狗狗 nl |犬类 >是状态的投射 |犬类 >关于清洁状态 |狗狗 nl >
当我们考虑到各州"买面包"的时候 |面包师>和 |面包师>我们隐含地认为,我们可以以无所谓的方式观察一个和另一个,也就是说,发生的概率相同。.
这就是所谓的等价交换状态.
但系统的特点可能使情况并非如此,例如,如果面包师比糕点师离家更近,而且天气非常寒冷,那么状态的概率 |面包师>将比国家的更强大 |面包师>.
这在下图中得到了体现,Ab大于Ap.
(A是概率振幅).
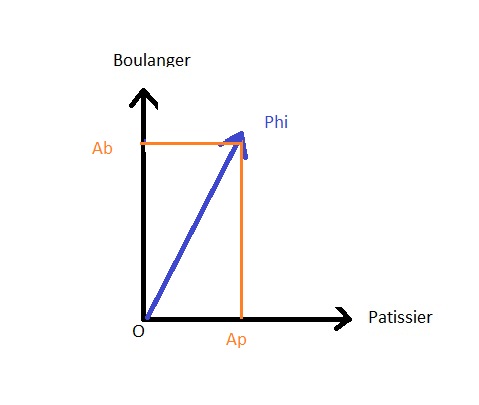 国家的预测 |菲>国家的总体情况 |面包师>的值为Ab,它对应于从一般状态获得该状态的概率振幅 |菲>同样适用于Ap,它是获得状态的概率的振幅 |面包师>.
国家的预测 |菲>国家的总体情况 |面包师>的值为Ab,它对应于从一般状态获得该状态的概率振幅 |菲>同样适用于Ap,它是获得状态的概率的振幅 |面包师>.
量子特征态总是正交的,也就是说,它们彼此成直角,因此按照 . Pythagore
为直角三角形.
"两边长度的平方之和,等于斜边长度的平方"。 在我们的例子中,斜边对应的是状态向量 |斐尔>和双方对 |斐尔>在两个特征状态上 |面包师>和 |纪念品>.
该定理说,波幅的平方是指概率.
考虑系统的一般状态意味着简单地考虑有:因此,系统的实际状态的概率总是等于1.
这就是公设所提到的,说国家 |斐尔>是规范化的,而且根据惯例它的规范总是等于1,因为它是一个概率.
在数学上我们注意到 <斐尔 |斐尔 > =1 = | |斐尔> |² (最后一个表达式表示矢量规范的平方,矢量的规范是它的长度。) 然后这个概率被分成几个较低的概率,对应于每个特征态,但有一个约束条件,即系统的特征态振幅的平方之和总是等于1,这是一定的概率。.
在我们的案例中,我们有:
Ab² Ap² =1 系统所有可能状态的概率之和必须等于1.
可以说,系统的存在遍布其所有存在的可能性,但没有任何存在的损失,所以它的存在被保存下来了。.
事实上,如果总概率降低,这将意味着该系统存在的机会减少,通过将其存在的概率降低到零,它将消失。 ! 状态或波函数的振幅可以是正的或负的,就像波的波峰或波谷一样。.
因此,概率振幅要么是负的,要么是正的,这就是我们在氢分子的结合态和非结合态的图片中用符号加号和减号表示的------。 .
(. états molécule hydrogène 毕达哥拉斯式) 但是,作为振幅的平方的概率 (或标准的平方 )因此总是正的,这对一个概率来说是正常的.
的确,我们可以想象一个确定的概率,然后是一个不太确定的概率,然后是一个不确定的概率,甚至是一个零的概率,但一个负的概率是没有意义的。.
另一方面,概率振幅可以是负的.
假设我们有两个相等的概率振幅,但符号相反,并向对方传播 (他们是波浪).
如果我们考虑当这些振幅在同一个地方时的概率,那么相反符号的振幅就会抵消,它们的平方也为零.
观察到的东西的概率将为零.
但如果振幅是分开的,它们的平方将是正的 (多多益善,但少少益善也是积极的。)因此,观察到的东西的概率将不再是零.
当我们谈论量子力学时,我们认为它的概率特性是一种机会游戏,但我们通常忽视的是,这些概率是由一些更令人不安的东西支撑的,这就是概率波的振幅,它使量子力学具有现实性。.
如果我们考虑表达式 |犬类 L ><犬类 L | 由 \"Ket \"和 \"Bra \"组成,适用于 \"Ket\"。 |犬类 > 我们得到 |犬类 L ><犬类 L |犬类 > 其中 <犬类 L |犬类 > 是获得状态的概率振幅 |犬类 L > 所以我们有 : |犬类 L ><犬类 L |犬类 > = |犬类 L >ǞǞǞ =ǞǞǞ |犬类 L > 我们看到,最终的状态是 |犬类 L > 与概率相关的 ǞǞǞ 表达方式 |犬类 L ><犬类 L | 因此,是一个改变了初始状态的操作者 |犬类 > 到最终状态 |犬类 L > 而这一概率为 ǞǞǞ.
它是一个演化算子,在观察过程中使系统演化到约束能量状态.
这很自然地把我们引向第五个公设,它描述了系统在测量过程中的演变情况.
考虑以下运算符:
|犬类 L ><犬类 L | |狗狗 nl ><狗狗 nl | 这是对一个可观测的特征态的演化算子的总和 (这里的能量 :绑定和非绑定状态).
如果我们将这个算子应用于ket |犬类 >在一个 :
( |犬类 L ><犬类 L | |狗狗 nl ><狗狗 nl | ) |犬类 > 或 |犬类 L ><犬类 L |犬类 > |狗狗 nl ><狗狗 nl |犬类 > 这导致了 |犬类 L >ǞǞǞ |狗狗 nl >Anl 甚至是 ǞǞǞ |犬类 L > Anl |狗狗 nl > 这是对状态的分解 |犬类 >在其自身能量状态的总和中 |犬类 > =ǞǞǞ |犬类 L > Anl |狗狗 nl > 操作员没有改变状态 |犬类 >而是简单地将其分解为各个部分,为此,它被称为"单位分割算子"。.
值得注意的是,状态的矢量表示及其根据正交基础的分解可以自然地表示概率的振幅,从而在测量过程中系统演变的概率。.
Postulat_V
衡量标准 :波包还原 如果在时间t,对由矢量代表的系统进行物理量A的测量 |斐尔>的结果是特征值An,那么测量后系统的状态立即被投射到与An相关的特征空间上。 这个定理也被称为"波包还原定理"。.
首先,让我们来阐释一下这个"子特征空间"的概念.
它只是将状态分解为其特征状态的一般化.
让我们回到有两个面包师和一个糕点师的面包例子上.
如果无法观察到贸易类型的区别 (不是系统的可观察因素)在测量的情况下,不需要区分是面包师1还是面包师2,只要知道状态被投射到面包师自己的子空间就足够了,事实上,在下图中,它对应于面包师所居住的水平面 ! 如果有一种可观察的东西允许我们观察面包是从哪个面包师那里买的,在这个测量过程中,状态将被投射到某个面包师那里,从而解除测量的不确定性。.
但如果系统的这一属性没有被观察到,那么系统仍然处于这种贝克波函数的叠加状态.
该状态被说成是变质的.
在实践中,当几个特征态具有相同的特征值时 (同样的能量)已经说过,这些状态是退化的.
通过对系统施加一个额外的能量约束,改变退行状态的能量,使其不再相等,退行现象就会被消除。.
量子物理学本质上关注的是理解微观世界的结构,而微观世界本质上是由谐振构成的。 (驻波)它们是系统总能量算子的特征状态 (汉密尔顿).
 第五条公设指出,在测量过程中,系统的状态会向其特征值被测量的状态演变.
第五条公设指出,在测量过程中,系统的状态会向其特征值被测量的状态演变.
正是这个所谓的"波包还原"或"波函数坍缩"的定理,使矢量投影的几何表示具有物理现实性,因为系统在这个操作中物理地演化了.
这可能是量子力学最伟大的概念革命,引入了对系统的观察导致其演变的事实,而在非量子物理理论中,只有动态方程负责系统的演变。.
传统上,机械理论的动态方程表达了能量如何作用于系统,使其发生转变.
在这第五条公设中,我们已经看到,测量本身改变了系统.
在量子力学的情况下,这样的动态方程也存在,被称为 薛定谔方程 .
因此,在力学上,有两种进化机制:时间内能量的作用和时间外观察的作用.
正是这个方程构成了量子力学的第六个也是最后一个定理 (见下文).
第五个公设涉及系统的观察者在系统的演化中的作用.
因此在量子力学中,观察者不再是独立于物理系统的了.
观察者和物理系统构成一个不可分割的整体.
可以说,观察者被嵌入了系统中 (但不是在量子纠缠的意义上,它只涉及波函数).
我们在上面提到了量子纠缠现象,它产生于这样一个事实:由几个粒子组成的量子系统由一个单一的波函数来描述 (第一个假设)即使这些粒子很可能在物理空间中移走了.
根据第五项公设,在测量过程中,波函数塌缩到一个适当的子空间,同时影响到组成系统的所有粒子的状态。.
正是爱因斯坦正式不能承认的量子力学的这种含义,因为在他看来,它违反了由光速定义的任何物理相互作用的传播极限.
根据爱因斯坦的相对论,没有任何能量可以超过光速。.
光显然是以光速传播的,它能做到这一点是因为它是纯能量,即没有质量。.
因此,质量粒子必然以低于光速的速度运动.
这个量子悖论的"物理"解决方案是由一个被称为 \"的实验进行的。expérience_d_Aspect.
这个实验无可争辩地证明,波函数不依赖于我们所处的物理空间:它在由于观察而发生的塌陷过程中的演变在空间的任何一点上同时发生.
阿斯佩克特的实验在越来越复杂的条件下被多次复制,以将量子力学推向其极限,但它从未屈服。 ! 量子理论被说成是一种非局部理论.
所用的术语"非局部性"或"非分离性"是等同的.
因此,我们可以说,量子波函数超越了物理空间,它甚至超越了时空,因为自爱因斯坦的相对论以来,我们必须将空间和时间视为同一更深层现实的方面。 :时空连续体.
继阿斯佩克特的实验之后,最近在相对论框架下进行的一项实验证实了量子纠缠在相对论框架下的有效性.
(cf Expérience_d_Antoine_Suarez在该物理学家的网站上发现 Philippe_Guillemant它提供了一个整合量子现实的愿景 ) 这最后一个实验很重要,因为在物理实验中,人们只能在一定范围内测量数值.
因此,在第一个Aspect实验中,相关光子的检测器 (在一个单一的量子态中)相距只有几米.
这足以证明,量子纠缠不可能是由未知的物理现象造成的 (隐藏变量)以亚光速.
这种现象的速度必然是超光速的.
尽管由于爱因斯坦的相对论,这样的超光速很难被接受,但阿斯佩克的第一个实验并没有完全否定这种可能性.
安托万-苏亚雷斯的实验是这样做的,因为它甚至抑制了两个相关光子的检测之间的因果关系的可能性,因为检测所处的相对论参照系不允许有"前"和"后",这是因果关系的基本条件:两种光子都没有被检测到,因为这些检测不是在相同的时间范围内进行的。.
因此,在相对论的量子理论中,波函数不能再依赖于时间,正如我们在第一个公设中看到的那样.
原因是,时间被降低到与位置相同的水平,即系统的可观测属性,而波函数与系统的属性无关 (第二个前提).
在这样一个理论中,波函数将是 |犬类 >而不再是 |诗意(t) > .
时间将是一个可观察的T,与位置P的方式相同.
L_expérience_du_chat_de_Shroedinger是一个由物理学家设计的思想实验。 Erwin_Shroedinger思考与第五公设直接相关的量子力学中的测量问题.
这个用"真猫"提出的完全不现实的思想实验的特殊性在于让你思考量子力学中的观察者是什么?.
你已经在关于措施的定理中看到了 (或观察)我们并没有详细说明观察者是什么。.
这些假设说有一个进行测量的观察者,但对观察者的性质没有更多的说明。 ! 在这个实验中,一只猫被隔离在一个盒子里,这样它就不能被观察到。 (量化的)以任何方式.
这假设了猫可以被视为一个量子物体,而实际情况并非如此,尽管在理论上,猫可以被先验地视为一个物理系统,它是由原子组成的,并且被量子力学很好地描述了。.
在这个房间里还有一个小瓶,里面装有对猫来说是致命的气体,还有一个粒子检测器,如果检测到一个粒子就会打开小瓶。.
如果检测到一个粒子,猫就会死,如果没有检测到,猫就会活。.
只要我们没有观察到猫的健康状态"语气",它就一直处于一种一般的量子状态,被称为可观察的特征态的叠加,这些特征态是 |活猫 > 和 |聊天室 > 所以我们有 |聊天 > = |活猫 > |聊天室 > 我们的量子系统是由几个部分组成的:猫,探测器,粒子.
所有这些子系统在建立波函数时也必须加以考虑,因此我们有: |粒子 > = |粒子存在 > |不存在的粒子 > 和 |传感器 > = |探测到的状态粒子 > |未检测到的粒子状态 > 与量子力学相关的数学知识表明,我们将称之为"薛定谔"的全局系统是 : |碎碎念 > = |猫,探测器,粒子 > = |聊天>¤ |传感器 >¤ |粒子 > 其中¤是状态向量的"张量乘积"。.
由于它们被发现处于相同的量子态,这些不同的子系统被说成是错综复杂的.
这个产品的行为与普通的产品交易一样,它是可分配的。 :A * (B C ) =A*B A*C 因此,在量子方面,我们可以发展出一般的量子状态.
让我们从仅由检测器和粒子组成的系统开始吧.
|探测器,粒子 > = |传感器 >¤ |粒子 > = ( |探测到的状态粒子 > |未检测到的粒子状态 > )¤ ( |粒子存在 > |不存在的粒子 > ) 通过发展 :
|探测器,粒子 > = |探测到的状态粒子 > ¤ |粒子存在 >
|未检测到的粒子状态 >¤ |不存在的粒子 >
|未检测到的粒子状态 >¤ |粒子存在 >
|探测到的状态粒子 > ¤ |不存在的粒子 >
Erwin Shroedinger nweb 前两种状态很容易理解,如果粒子存在,那么它被检测到是合乎逻辑的,如果它不存在,就不会被检测到。.
以下两种状态是非常不可能的,但根据量子力学,一切都只是一个概率振幅,还是存在的.
对国家来说 |碎碎念 > 完成后,有必要进一步发展猫的状态,这将导致我们得到一个具有八个可能的特征状态的波函数,其中两个是高度可能的,六个是高度不可能的。.
两个可能的状态是:
|聊天室 >¤ |探测到的状态粒子 >¤ |粒子存在 > |活猫 >¤ |未检测到的粒子状态 >¤ |不存在的粒子 > 只要我们没有观察到这个系统,例如相当于打开盒子,我们就处于一种叠加状态,猫处于一种不确定的生命力状态。.
矛盾就在这里.
但我们可以进一步推理,这就是物理学家的做法 Eugène_Wigner诺贝尔物理学奖.
这就是 théorie_de_l_influence_de_la_conscience 他认为,观察者的眼睛看到猫的死活,也是一个有两种状态的量子系统: |橄榄油 > = |眼见为实 > |眼见为实 > 然后,完整的波函数的状态将考虑到"幻觉"的状态,在这种状态下,眼睛会看到死的,猫是活的...
但我们可以继续考虑测量链,直到观察者的大脑,它也是由原子组成的.
因此,问题是 :当测量实际进行时,即波函数的坍缩,从而选择实验的结果:死或活的猫.
维格纳说,没有任何物质可以引起坍缩,因为所有物质都容易被量子力学描述,因此是波函数的一部分,人们也可以很好地考虑宇宙的波函数.
如果没有任何物质的东西来操作测量,那就只剩下非物质的东西来操作,而这一点维格纳将其与意识相提并论,最终确定观察者是什么。.
在他的解释中 观察者就是意识 .
注意观察者和波函数之间的联系:这两点都不重要 ! 可以说,物质的东西是位于两者之间的东西。:观察.
这使我们更接近物理学家提出的"独立的现实"或"隐蔽的现实"的概念 Bernard_d_Espagnat对量子力学的哲学理解.
bernard_d_espagnat_physique_quantique_et_réalité_la_réalité_c_est_quoi ;检索自 \"https://www.
youtube.
com/watch?v=Jd8FiWJ5v8M; 这也使我们更接近古印度的吠陀观念,即把物质现实描述为"Maya"或感官的幻觉。.
这个玛雅是由三个元素之间的无限相互关系构成的 :richi、chandas和devatta是主体、客体和它们的关系、知识。 (精神:心灵的)或感知 (材料:的材料).
意识观察者和非物质的量子现实创造了现象学的物质现实.
在这方面,电影《黑客帝国》是一个现实的寓言,唯一不同的是,创造虚幻现实的不是机器,而是意识本身,这一点很重要。.
因此,意识可以被定义为主体通过感知或知识与客体的关系.
以下三段式是等价的:
samhita_tab_zh
维达 哲学 量子物理学
立志 主题 观察者 行家 观察者
devatta 感知 (主体/客体关系) 观察 知识 可观察的 昌达斯 对象 观察到的 已知 测量结果:观察者的特征值
波函数和意识代表了同一现实的两面,超越了物质性和
在这种物质性的起源处.
显然,物理学家作为一个整体,对量子现实的看法一般不会走得那么远。.
这个领域的标准位置是interprétation_de_l_école_de_Copenhague.
这个立场说,在两个测量之间没有物体,唯一存在的物体是"被观察的物体"。.
这一立场来自于人类观察者的情况,他们经历了一个经典的世界,并认为它是绝对的参考。.
经典一词对应的是整个人类以同样的方式感知到的东西.但这一立场与
量子现实,因此被认为是完全矛盾的.
可以定义与该位置的不同程度的距离:
- 第一度完全专注于这个位置,拒绝承认有其他的东西。
绝对客观的物质现实.这就是唯物主义的观点.
应该指出的是,自从阿斯佩克特的实验验证了力学,这种观点在科学上已经站不住脚了
在其最令人不安的声明中.
同时,这个量子力学是科学史上验证最多的理论.
这种观点因此被简化为一个简单的"唯物主义信念"。.
不过,这也是爱因斯坦的观点,但不幸的是,他没有活够,所以
看到阿斯佩克特实验解决了他与物理学家波多尔斯基和罗森在其著名文章中定义的悖论。:
的 Paradoxe_EPR.
- 第二个层次是对哥本哈根学派的解释,目前仍只有少数人知道。
少数人,主要是物理学家和哲学家的知情人.
在这里,我们所处的古典世界不再代表世界的全部,因为有
一个绝对陌生的量子世界,我们无法进入,但我们可以通过以下方式处理它
通过量子理论.
- 第三度认为,经典世界是由原子本身构成的粒子组成的
古典世界的基础是量子世界。
因此,它应该合法地成为绝对的参照物。.
我们知道的稳定的物理世界只由三个量子粒子组成:电子、质子和中微子.
这第三个观点消除了所有的量子悖论,最后简单地说,我们不能
不求解释 (经典)量子理论,但人们不得不接受它。
因为它是 (哥本哈根)并最终承认其地位的优越性.
因此可以预言,量子模型永远不会出现故障.自其诞生以来,人们已经越来越清楚地认识到量子现实是如何
在理解我们周围的世界,特别是在生命领域,一个具有高度一致性的宏观系统方面进行了干预。...量子.
最近的两个例子是:
Postulat_VI 量子态的时间演变.
国家 . Phi
任何非相对论的量子系统都是随时间变化的薛定谔方程的一个解:
_ H |菲(t)> =i h/2*pi d |菲(t)>/ dt _
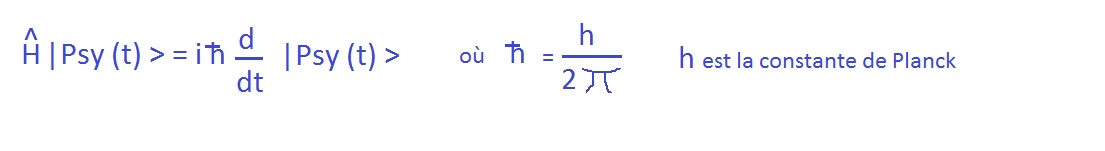 第六条公设是. équation de Schrödinger
.
第六条公设是. équation de Schrödinger
.
这就是量子力学的动态方程.
它只是意味着,它是系统的 \"总能量 \"算子,或哈密尔顿,注意到"H",它对系统在时间上的演变负责.
(传统上,在量子力学中,算子被赋予一个帽子,以区别于其他数学对象,如特征值.薛定谔方程) 方程的形式表明,通过将哈密尔顿算子应用于系统的波函数,我们可以得到其相对于时间的导数,即它在时间上的变化情况.
(对于时间的delta t变化,所以"dt"我们有一个变化"d |诗意(t) >"的波函数).
因此,如果我们应用汉密尔顿算子 (能源)我们得到了它在时间上的演变。.
很明显,是能量使事情发生。.
能量和时间是有内在联系的.
它们被称为形成一对共轭变量.
这个方程只在非相对论的框架内有效.
在相对论框架下,有效方程是克莱因-戈登方程.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf 哈密顿算子H是由介入系统的所有能量组成的.
这些能量有两种:动能和势能.
动能是指运动的质量中所包含的能量.
扔进窗户的小石子,在给定的速度下,凭借获得的动能将窗户打碎。.
如果有几个连续的玻璃板,石头的速度越大,它将通过的玻璃板就越多。.
势能是由于适用于系统的力场造成的.
如果一个小石子掉在地上的窗台上,它将获得速度,因为它与地球的距离使其拥有的重力势能。.
时间越长,势能转化为动能的越多,当小石子到达地面时,它凭借获得的动能打破了窗户,而它失去的势能却被削弱了。.
如果你把它推入井中,它将继续同样的过程,直到它的势能完全耗尽,如果这有可能的话。.
如果我们考虑钟摆的运动 (鹅卵石)后者摆动,即从起始位置 (与垂直方向成一定角度)鹅卵石掉落的地方,鹅卵石会加速,直到绳子垂直,然后减速,直到它停在另一边与起始位置对称且垂直的位置。.
摆子将其势能转化为动能,再将其动能转化为势能,这样循环往复.
如果系统不受任何其他力的影响,运动不会停止.
在实践中,总是有摩擦力将能量耗散成热能,直至耗尽。.
但这最后一点只在经典力学中是正确的,因为在量子力学中没有摩擦。 ! 另一个在势能和动能之间存在循环转换的系统是卫星围绕行星的运动,例如月球和地球。.
在这种情况下,经典力学的解决方案表明,卫星的轨迹是一个椭圆,也就是说,有一个时刻,当月亮离地球最远的时候 (最大势能和最小动能,远地点)和另一个时间,当月球离地球最近的时候 (最小势能和最大动能,近地点).
我们刚才描述的系统是经典系统,但它们在量子领域有其对应关系.
例如,量子力学中的钟摆模型被称为谐波振荡器,卫星模型对应于氢原子模型:质子的电子卫星.
在量子力学中,动能是一个涉及质量的算子,而势能当然也由一个算子表示,其形式将取决于所涉及的能量:电、磁势。 ...
质量参与薛定谔方程的方式,来自于路易-德-布罗格利的早期工作,他建立了波-体二象性:对于每一个物质粒子,我们可以联想到一个频率与质量成正比的波。.
这是以两个能量公式为基础的:E =m c²,这是爱因斯坦的狭义相对论的能量公式 :的质量相当于能量E =h * nu,这是解释光电效应的普朗克-爱因斯坦关系。 :能量与频率成正比.
因此我们看到,在薛定谔方程中,集成了爱因斯坦狭义相对论的一个结果.
重要的是要理解,所涉及的能量对系统施加了一个约束,即对波函数的约束.
在处理震荡系统时,如谐波震荡器 (铅笔盒)或氢原子 (卫星)能量约束的效果是将波函数定位在一个空间区域内.
例如,一个不受力的经典系统 (迷失在星际空间的流星,那里的恒星引力可以忽略不计。)将会无限期地直线移动.
量子等价物是一种无限期传播的平面波,例如不受任何力影响的光子。 (光子是没有质量或任何种类的电荷的粒子,因此不受任何力或能量的影响。).
当波函数有一个循环解时 (本地化波函数)时间不再具有使系统的各部分无限期地远离对方的效果.
电子将保持在靠近其原子核的位置,在氢原子的情况下是质子。.
同时,如果量子波在有限区域内循环传播,它就会与自己重叠,因此会与自己发生建设性或破坏性的干扰.
在求解这类系统的薛定谔方程时,可以看到时间不再介入波函数的形式,只有空间 (位置)这决定了波的形状.
这种情况是 ondes_stationnaires_zh这一点已经提到了.
这就是说,干扰具有建设性的地方总是与干扰具有破坏性的地方相同。.
驻波是一个强大的概念,它使我们能够理解一个静态现象是如何从动态现象中产生的.
这是允许整合量子观的要素之一:我们所体验到的物质的所有稳定性都来自于不断运动的波的纠缠,但其干扰结果是稳定的。.
对于原子来说,这给出了定义明确的轨道,其形状由薛定谔方程的解函数提供,即原子轨道: 这些云是电子存在的概率的云.
云层越密,电子出现的概率越大.
 驻波的概率振幅的表示方法 (谐波)的谐波振荡器.
驻波的概率振幅的表示方法 (谐波)的谐波振荡器.
注意与振动状态的相似性 (振动结点和腹部)振弦之声.
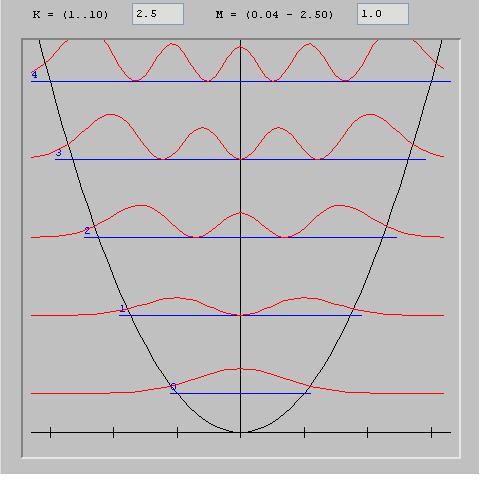
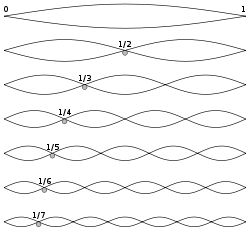 我们注意到,在量子情况下 (左边)波函数的概率振幅 (红色的)随着人们远离中心而逐渐减少,即在电位变得更强的地区 (黑色的抛物线)但从未完全为零.
我们注意到,在量子情况下 (左边)波函数的概率振幅 (红色的)随着人们远离中心而逐渐减少,即在电位变得更强的地区 (黑色的抛物线)但从未完全为零.
因此,粒子有可能在势能高于动能的遥远区域被发现,而传统上它会被困于势能低于动能的区域。.
这一事实是导致effet_tunnel它允许量子粒子穿过能量高于粒子能量的势垒,因为势垒另一侧的波函数不为零,允许粒子在那里被观察到。.
这是波函数的非局部方面的结果.
这是能量对波函数施加的约束,使其保持本地化,从而与自身相互作用,产生与特定能量值相关的驻波。 (因此,量化的价值)这就是"量化"概念的起源.
最后,有必要谈一下量子理论的起源是什么:的 constante_de_Planck这出现在薛定谔方程中.
这个常数是由物理学家提出的 Max_Planck以解释物质的热辐射值与温度的关系.
这种辐射所遵循的观察规律迫使我们考虑,热能不是连续发射的,而是以数据包或"量子"的形式发射的。.
这是物质的量子性质的第一个证据.
在物理学中,行动被定义为能量和时间的乘积。.
它是相当直观的:当一种能量在一定时间内起作用时,它产生一定的作用,其值与能量的值和它起作用的时间长度成正比。.
普朗克常数代表物理世界中最小的可能行动.
它是物理学的一个普遍常数,是现实的量子性质的特征。.
这个常数的值是非常小的: 6.62607004 × 10-34 m2 kg / s 但它仍然是非零的.
0,000000000000000000000000000000000662607004 当这个常数与其他基本常数如光速或万有引力常数相结合时,可以推导出不同物理学单位的最小数量 :普朗克长度,普朗克时间,等等。...
这被称为普朗克单位.
因此,量子力学所描述的物理世界在无限小的范围内有一个极限,超过这个极限我们就不能再用物理学来说话,它最终是物理世界的一个边缘.
如果有一个边缘,一个极限,它是波函数的一个自然的量子约束,因此也是量子化的一个约束 (正如我们所看到的,这本身就是一种力量).
普朗克常数定义了宇宙的像素化.
量化的最根本起源也可以在意识的运作中找到,而意识在本质上是不连续的.
事实上,如果我们考虑一个主体对作为意识中的一个观点的对象的观察,这只有通过对不同的可能的观点的意识的区分才有可能.
为了使它们被识别,观点必须是截然不同的,否则所有的观点都会合并,就不会有真正的观察。.
辨别力是智力的品质,在这个意义上,它是意识的一个基本属性。.
因此,我们发现存在于测量的量子定理中的元素.
以下是将所有的假设合并为一个箴言的尝试:
"在良知的注视下,有可能完成的事情才会被完成.
"
1.5.1.箴言的分析
诗 量子匹配 链接到定理
什么是 波函数或状态向量或"ket" (来自支架,法语中的钩子) . Premier postulat
可能的 波函数的概率结构,不同可能性的特征态的酮体 . Troisième postulat 完成了 负责演化的系统的哈密顿算子总能量的动态变化. . Deuxième postulat 在良知的注视下 测量的假设,即观察者的必要干预 . Quatrième postulat 惟其如此,方能成事 只有可观测的特征值可以得到,那么系统的状态就是相应的特征状态. . Cinquième postulat 可能的事情已经完成 薛定谔方程,量子力学方程. . Sixième postulat
量子力学是我们现代科学时代最伟大的革命,因为它明确地摧毁了唯物主义的立场,从而为人类的发展开辟了道路,科学和意识将重新结合在一起。.
科学家们在接受量子理论的信息方面有很大的困难,这也解释了为什么很少有人能接触到它。.
在此,你将看到由Jean Staune分析并由Bruno Lussato报道的这一情况的摘要。: bruno_lussato_les_plus_grandes_désinformations_de_l_histoire_des_sciences
(2009年,我在博客上留下了关于阿兰-阿斯佩克1982年在图卢兹举行的会议的记述,当时他正在法国的大学里巡回演讲,介绍他的工作成果.布鲁诺-卢萨托:科学史上最大的错误信息 nweb) 这篇文字本可以由大量属于科学"建制"的有识之士来写,而且可能写得更好,但他们不愿意这样做,一方面使我能够保留域名量子.
另一方面,我花了几十个小时来阐述这个可能仍有待改进的文本。...
解决爱因斯坦-波多尔斯基-罗森模仿的决定性实验
由奥赛量子光学中心的研究员和实验者阿兰-阿斯佩克特于1982年制作的。
是以光子为基础的.
对基础理论的详细描述可以在《中国的世界》一书中找到。 作者:Bernard d'Espagnat "A la recherche du réel".
同一年,我在大学里,阿兰-阿斯佩克特来介绍
在图卢兹,在保罗-萨巴蒂尔大学的麦克斯韦圆形剧场,它的结果是这样的.
在提出明确的测量结果后,他离开了
无声的集会 (讲堂上坐满了教授和研究人员).
在演讲结束时,在一段重要的沉默时间后,当开始发言时,发言者说 在大会上,只有一位研究人员站了起来 (我的相对论老师)并提出这个问题:
而你现在觉得很容易接受这个事实吗?.
阿斯佩克特在辩护中回答说,他没有这样说过,他已经做了
实验,结果是这样的,但他很注意不要
作出任何解释.
多年后,我从一个曾经和他在一起的人那里得知,他是
亲爱因斯坦的人,他曾预计量子力学会受到挑战.
我在第三排的边厢里,独自一人,我感到很好笑,因为我不明白
为什么他们有问题,或者说我太明白了.
当实验处于起步阶段,但结果只是时间问题。
争论已经变得非常强烈,甚至充满了硫磺味.
当物理学家的科学界处于震惊之中时,我们
不知道会发生什么.
信息的消化需要时间,我们可以在2020年看到,形势 已经有了相当大的发展,看看这个在巴黎综合理工学院的讲座就知道了。 作者:Hervé Zwirn,国家科学研究中心的研究主任
_x_sciences_de_l_homme_et_de_la_société_x_shs_mécanique_quantique_le_monde_existe_t_il
这一经历对 (或者说,对于大多数人来说,应该有)的同类效果。
物理学家认为,无线电波的发现 (电磁波)有的人
赋予抽象的电磁场概念以更生动的现实意义.
不可分离性的发现及其在
物理层面赋予独立现实的概念以生命,即
一个独立于空间和时间的现实,即所有的
时空突发事件,即所有物理突发事件.
从力学的第一个公设可以得出的第一个结论是 就是说:
量子系统的现实 (而最终,所有的系统都是量子化的!X 人类和社会科学 X Shs 量子力学 世界是否存在 Nwebs)的基础是
由一个本身无法观察到的抽象的可能性空间来决定。 (非物理性的和
不受所有时空突发事件的影响)但仍然是真实的,因为它是
从这个抽象的功能层面,具体的现实出现了 (观察到的).
用一个词来概括它:它是无所不在、无所不晓的,因为它包含了
以非本地方式提供关于物理系统的所有信息.
此外,为了完整起见,这与观察者有关,这显然不可能是物理的.
这些假设显然不包括物理系统中的观察者
但宣布它的存在对于观察的发生或对于一个人来说是必要的。
产生物理结果.
很明显,观察者和独立的现实有一种密切的关系:
它们都是非物质性的,并在信息、知识、感知方面相互作用。.
这与萨满们对"世界之梦"的构想完全吻合。.
在这方面,电影《黑客帝国》可以被看作是量子现实的一个寓言。.
与现实的区别在于,全息模拟的世界不是制造出来的
是由物质的计算机,而是由非物质的宇宙计算机,它确定自己是
在最广泛的概念中对意识的认识.
这个宇宙意识可以而且已经被赋予了任何你喜欢的名字
但这些将永远不会耗尽这个意识的无限力量.