I postulati della meccanica quantistica
versione disponibile in : en ru zh es ja de nl pt fr
data di creazione : 20240129- data di aggiornamento : 20221007- data di generazione : 20241110_231431
Questo articolo presenta in dettaglio il postulats_de_la_mécanique_quantique da semplici considerazioni matematiche e geometriche e da analogie tratte dalla vita quotidiana.
In fisica, i concetti relativi agli oggetti matematici sono sviluppati per stabilire teorie che permettono di rappresentare il mondo fisico attraverso le sue leggi di funzionamento..
La meccanica classica o teoria di Newton è la teoria che ci permette di rappresentare il funzionamento della materia su scale sensibili alla percezione umana, che chiamiamo macroscopiche..
Su scala cosmologica questa teoria è generalizzata attraverso le teorie relativistiche di Einstein.
La relatività generale è la teoria che tratta in modo più completo la forza di gravità ..
La meccanica quantistica è la teoria che ci permette di rappresentare il funzionamento della materia a livello microscopico, anche se il confine tra il microscopico e il macroscopico non è chiaramente definito in termini di scala, per cui possiamo avere comportamenti quantistici a scale macroscopiche, come nella laser o il cables_électriques_supraconducteurs La teoria quantistica non si occupa di una particolare forza della natura, come la relatività generale, ma è piuttosto un linguaggio.
Il linguaggio degli oggetti quantistici.
Possiamo quindi applicare questo linguaggio a varie forze o sistemi, quantificandoli..
L'insieme dei concetti quantistici ruota intorno a sei postulati fondamentali che definiscono compiutamente la teoria quantistica.cavi di potenza superconduttori nweb Presenteremo questi sei postulati e cercheremo di identificare il loro significato in modo semplice.
L'espressione del primo postulato, come definito nel libro di Cohen-Tanoudji " Meccanica Quantistica Volume 1" è :
Ad un tempo fisso t, lo stato di un sistema fisico è definito dai dati
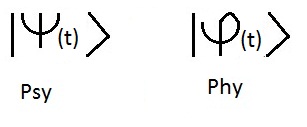
di un ket o di una funzione d'onda o di un vettore di stato notato |psy(t)> appartenenti allo spazio degli stati".
Postulato I nweb
La lettera greca Psy viene utilizzata per indicare la funzione d'onda, noi usiamo
anche indifferentemente la lettera Phy.
Il primo concetto di meccanica riguarda la rappresentazione dello stato del sistema fisico.
Questo è un modo naturale di definire l'oggetto dello studio.. Qui diciamo semplicemente che il sistema esiste
e che il suo stato può essere rappresentato da una funzione dipendente dal tempo
Questo perché lo stato del sistema non è a priori statico, ma dinamico..
In meccanica classica, il sistema fisico è rappresentato dal ^punto materiale"..
Un sistema complesso sarà rappresentato da un insieme di punti materiali collegati tra loro.
tra di loro per formare un oggetto solido o non solido. (connessioni rigide o non rigide, ad es.: cristallo o gas).
Il primo postulato afferma semplicemente che lo stato del sistema in un dato momento è unico.
e appartiene a un insieme di possibili stati raggruppati in un insieme
matematica chiamata \"spazio degli stati\"..
Parliamo di spazio e non semplicemente di un insieme perché lo stato quantistico è un vettore
che è un oggetto matematico che rappresenta una direzione in uno spazio.
Tutti conosciamo lo spazio tridimensionale (lunghezza, larghezza, altezza o profondità , a seconda dell'orientamento delle prime due dimensioni)
È lo spazio fisico in cui viviamo.
Lo spazio degli stati in cui vivono i sistemi quantistici non è uno spazio fisico, ma uno spazio astratto. (Spazio di Hilbert)
e la sua dimensione è infinita per rappresentare l'infinità di stati possibili che esistono anche per sistemi fisici semplici.
Facciamo un'analogia con un esempio tratto dalla vita quotidiana
capire come viene modellato un sistema quantistico.
Immaginate una persona seduta tranquillamente nel proprio appartamento e che all'improvviso
si rende conto che deve uscire per comprare il pane.
Si prepara ad andarsene e nella sua mente c'è ancora qualche esitazione sul posto.
dove va a comprare il pane.
Può scegliere tra un panificio più avanti nella strada o una pasticceria che fa anche
che si trova più in basso rispetto a lei.
Scendendo le scale per uscire, si può dire che ci sono due stati possibili nella sua mente che corrispondono alle due opzioni di comprare il pane. Queste opzioni possono essere annotate in modo quantistico:
stato 1: |fornaio>
stato 2: |pasticciere>
Lo stato d'animo della persona è una combinazione di queste due possibilità :
| Stato> = |fornaio> + |pasticciere>
I due stati sono completamente incompatibili: o compra il pane dal fornaio o dal pasticciere. Entrambe queste possibilità hanno nulla in comune, non condividono nulla. Geometricamente si dirà che sono ortogonali (perpendicolare) e rappresentazione geometrica nello spazio (degli Stati così) sarà :
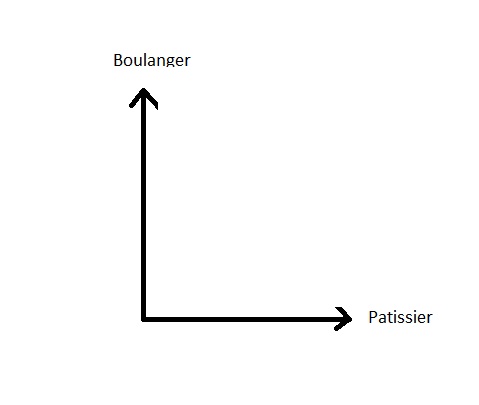
Abbiamo quindi due direzioni ben distinte, che non hanno nulla in comune.
Se la freccia (vettore) Baker era orientato verso la freccia (vettore) pasticciere
allora significherebbe che l'acquisto da
il fornaio è un po' legato all'andare a comprare
in pasticceria, che non è il caso, sono due
opzioni incompatibili: ortogonali, cioè ad angolo retto: non condividono nulla in termini di leadership.
D'altra parte, lo stato del sistema, cioè lo stato mentale, è un'altra cosa.
della persona è una cosiddetta combinazione lineare dei due stati.
Diciamo che abbiamo una miscela di stati. Il vero stato misto non
non corrisponde a nulla di osservabile: non lo sappiamo
non dove si compra il pane.
La combinazione lineare delle due possibilità corrisponde a
alla somma dei due vettori che rappresentano gli stati osservabili.
La somma di due vettori è realizzata come segue : lo facciamo
Dalla fine del primo vettore e del secondo vettore
somma risultante dall'inizio della prima e che termina verso la fine
del secondo.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
Lo spazio degli stati è stato definito uno spazio vettoriale, cioè uno spazio di direzioni, ciò implica che nella rappresentazione geometrica possiamo spostare i vettori senza modificarli natura, rimangono gli stessi vettori: puntano nella stessa direzione. Anche per semplificare nella rappresentazione, tutti i vettori vengono fatti partire dallo stesso punto per indicare che solo le direzioni esistono in questo spazio. Questo è chiamato spazio vettoriale in contrapposizione a ad uno spazio di punti che in matematica è chiamato spazio affine. ( Lo schermo sul quale che state leggendo questo testo è un esempio di spazio affine in cui i pixel rappresentano i punti di quello spazio.vettore somma di stati img)
La rappresentazione geometrica avviene ovviamente in uno spazio di punti, perché uno spazio vettoriale
è una pura astrazione e può essere rappresentata solo nello spazio che percepiamo con i punti (posizioni) diverso.
Ma questo non esiste nello spazio degli stati, dove tutte le rappresentazioni di un vettore a diverse
le posizioni nello spazio di rappresentazione corrispondono a un singolo vettore nello spazio vettoriale.
Pertanto lo stato può essere rappresentato come segue :
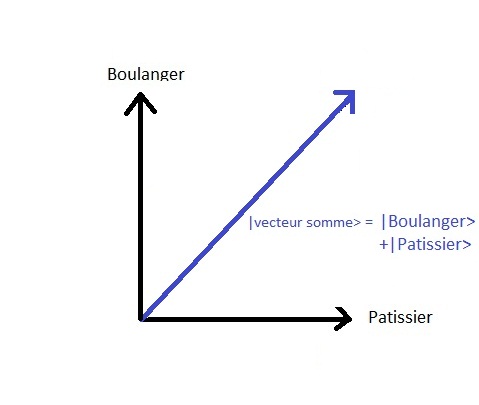
Qui la dimensione dello spazio degli stati è di due. Se ci fosse una terza opzione
con un altro panettiere in una strada adiacente | fornaio2 > allora lo spazio degli stati sarebbe di dimensione tre, ecc..
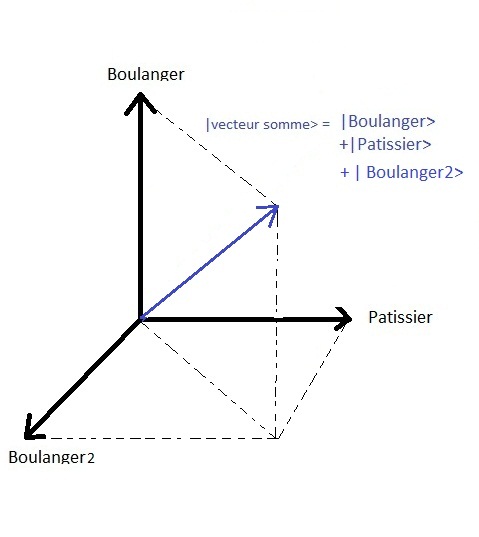
In fisica, i sistemi a due stati possono essere modellizzati allo stesso modo.
Questo è il caso della molecola di idrogeno ionizzato. La molecola di idrogeno
è composto da due nuclei di idrogeno, cioè da due protoni
e il fatto che sia ionizzato significa che un elettrone è stato rimosso da esso
dei due possiede naturalmente. Per esempio
perché è semplice : ad un singolo elettrone..
I due possibili stati posizionali dell'elettrone sono :
La rappresentazione geometrica è:
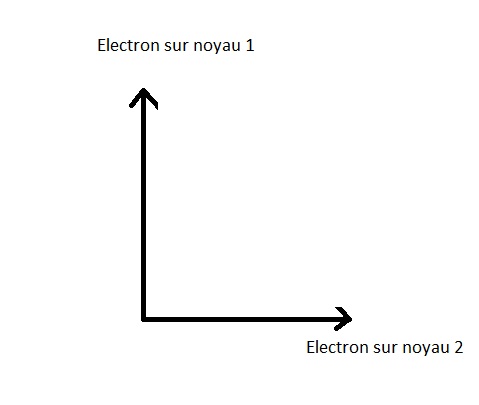
È chiaro che l'elettrone non può essere trovato (o piuttosto di essere trovato, ossia : essere osservato) contemporaneamente sul core 1 e sul core 2, questi stati sono ortogonali.
Nell'espressione del postulato, si utilizzano sinonimi per designare il vettore di stato, che viene chiamato indifferentemente
vettore di stato, funzione d'onda o ket. Questi diversi nomi corrispondono a diversi aspetti matematici del vettore di stato..
Vedremo l'aspetto della funzione d'onda nella spiegazione del secondo postulato e l'aspetto del ^ket" nel terzo..
In sintesi, lo stato quantistico è rappresentato da un dato vettore (direzione) in uno spazio vettoriale (delle direzioni),
questo vettore è chiamato ^vettore di stato^.
Nella meccanica classica, lo stato è rappresentato dal ^punto materiale" che è definito dalle sue proprietà fisiche posizione e velocità .
È importante notare che nella meccanica quantistica lo stato del sistema è totalmente indipendente dallo stato del sistema.
le proprietà fisiche del sistema. Lo stato è definito in modo astratto e si potrebbe dire \"non fisico\"..
Ciò sarà illustrato in dettaglio nella presentazione dei seguenti postulati attraverso la nozione di ^base di rappresentazione del vettore di stato"..
Ma si può notare che il primo postulato fa dipendere il vettore di stato solo dal tempo e non dalla posizione
che è lo spazio. Ciò significa che la funzione d'onda non è locale..
Ovviamente la relatività ci insegna che il tempo e lo spazio formano un continuum e quindi se una formulazione di
La meccanica quantistica tiene conto almeno della relatività speciale, il vettore di stato non dipende da
del tempo. Questa teoria è l'elettrodinamica quantistica o teoria quantistica del campo elettromagnetico..
La relatività speciale è molto legata all'elettromagnetismo per il fatto che Einstein ha elaborato questa teoria.
per eliminare i paradossi che la teoria elettromagnetica di Maxwell sollevava.
I concetti quantistici non sono stati concepiti per pura immaginazione. Piuttosto, sono stati forgiati nel fuoco della sperimentazione.
della microfisica che richiedeva la corretta rappresentazione di questi concetti..
Sebbene sia totalmente astratto, lo stato quantistico è comunque reale..
È questa realtà dello stato quantistico che spesso resta la cosa più difficile da ammettere, anche se è inevitabile.
Il funzionamento della materia, che è la cosa più concreta, è governato da qualcosa di totalmente astratto..
Tuttavia, è impossibile aggirare questa difficoltà , poiché questo concetto quantistico è straordinariamente solido..
La situazione cognitiva è in qualche modo simile alla scoperta delle onde elettromagnetiche. Queste onde sono state prima teoricamente
scoperto combinando le equazioni di Maxwell che descrivono i campi elettrico e magnetico.
La loro combinazione ha fornito un'equazione di propagazione delle onde con velocità costante. Era una nozione astratta
e nuovi, ma gli esperimenti hanno dimostrato che i campi elettrici e magnetici producono effettivamente onde
che potevano essere controllati e utilizzati, il che ha portato alle comunicazioni radio.
Abbiamo visto che questa velocità è la velocità misurata della luce.
Allo stesso modo, il concetto molto astratto di funzione d'onda è diventato molto concreto inintrication_quantique e ha dato origine all'area tecnologica di cryptographie_quantique
Postulat_II
Ogni quantità fisica osservabile 'a' è descritta da un operatore 'A' che agisce nello spazio degli stati.; questo operatore è un osservabile.
" Nella meccanica classica abbiamo visto che sono le proprietà del punto materiale, la sua velocità e la sua posizione a determinare il suo stato..
Ad esempio, la velocità e la posizione di una pallina su un campo da tennis o di un pianeta nel sistema solare..
La posizione e la velocità di un oggetto macroscopico sono determinate ad ogni istante e questo definisce completamente lo stato del sistema..
L'evoluzione della pallina da tennis nello spazio definisce in ogni momento lo stato del gioco, se la pallina è in movimento, "out" o no o immobile a terra dopo aver preso la rete..
Ed è la storia dei suoi Stati a definire la partita e il suo esito..
D'altra parte, in meccanica quantistica, lo stato generale di un sistema ridotto a una particella, come l'elettrone dell'esempio precedente, non è più associato a una particolare posizione o velocità , ma a un insieme di tutte le possibili posizioni o velocità ..
Inoltre, non possiamo osservare tutte le proprietà del sistema allo stesso tempo, come avviene nella meccanica classica..
Se il sistema è in uno stato posizionale, non è in uno stato energetico e viceversa..
Nell'esempio del pane abbiamo degli stati posizionali che sono il panettiere e il pasticcere, che indicano il luogo in cui il pane viene acquistato, ma come vedremo non sono stati energetici..
Come nell'esempio della molecola di idrogeno, il fatto che l'elettrone si trovi sul nucleo 1 o sul nucleo 2 rappresenta degli stati posizionali, ma questi non sono di per sé stati energetici della molecola..
In un sistema quantistico le diverse proprietà condividono lo stesso spazio di stato, ma gli stati corrispondenti alle diverse proprietà non sono necessariamente rappresentati dalle stesse direzioni nello spazio..
Ciò significa che se lo spazio è bidimensionale, ci saranno due possibili stati posizionali ma anche due possibili stati energetici e che gli stati energetici non hanno le stesse direzioni degli stati posizionali..
Nel caso della molecola di idrogeno (ionizzato) i possibili stati energetici sono:
| Stato:energia> = |Stato correlato> + |stato non vincolato>
nella rappresentazione ^dinamica o energetica" della molecola di idrogeno.
Lo stato generale del sistema è completamente indipendente dalle sue proprietà , quindi per il pane possiamo scrivere:
| Stato> = |determinazione> + |rinuncia> = |fornaio> + |pasticciere>
Per la molecola di idrogeno chiamando El (Stato correlato) e Enl (stato non vincolato) gli stati energetici e P1 e P2 gli stati di posizione, abbiamo:
| Stato> = | Il > + | Enl > = | P1 > + | P2 >
Il fatto che lo stato sia indipendente dalle sue proprietà osservabili e possa essere espresso indipendentemente da esse è una caratteristica fondamentale della meccanica quantistica..
Le proprietà sono rappresentate da operatori matematici che, applicati allo stato quantistico, determinano gli stati possibili per quella proprietà ..
Un operatore in matematica è ciò che fa evolvere un valore in senso lato.
Ad esempio, per l'addizione l'operatore "3 " applicato a "2" dà "3 2"="5" abbiamo cambiato il valore da "2" a "5" applicando l'operatore "3 " (aggiunta del valore tre) In meccanica quantistica l'operatore fa evolvere lo stato.
Il postulato dice che l'operatore "agisce" sullo spazio di stato.
Sia P l'operatore di posizione e E l'operatore di energia. (in realtà l'operatore energetico è indicato con H per hamiltonien_it che è la funzione energia totale definita in meccanica generale da Hamilton come la somma di tutte le energie che agiscono sul sistema).
Secondo il secondo postulato, questi operatori rappresentano le corrispondenti proprietà (posizione ed energia) del sistema.
Applicando (far funzionare le cose) l'operatore di posizione sullo stato della molecola di idrogeno abbiamo:
P | stato > = | P1 > o P | stato > = | P2 >.
Applicare l'operatore sullo stato significa osservare la proprietà corrispondente all'operatore, in questo caso la posizione.
Allo stesso modo con l'operatore energetico.
H | stato > = | Il > o H | stato > = | Enl >.
Possiamo vedere che quando applichiamo un operatore a uno stato, facciamo evolvere questo stato verso uno stato appartenente a questo particolare operatore, che chiamiamo stato Stato pulito dell'operatore.
Il risultato può essere qualsiasi stato possibile per il sistema e per l'operatore. (la proprietà misurata).
Lo Stato Molecola legata... è un autostato dell'operatore energetico, mentre l'autostato Un elettrone sul nucleo 1. è un autostato dell'operatore posizione.
Per la molecola di idrogeno allo stato legato, l'elettrone si trova in una posizione indeterminata tra i due nuclei di idrogeno..
Si può dire che l'autostato energetico è una combinazione lineare di stati posizionali, che può essere rappresentata come:
| Il > = | P1 > | P2 >
Si può dire che i due stati posizionali si sommano ad uno stato energetico: quando l'elettrone è condiviso dai due nuclei, la molecola è legata, si dice che i due stati posizionali interferiscono costruttivamente per formare lo stato energetico " legato".
allo stesso modo in cui lo stato non vincolato sarà rappresentato da | Enl > = | P1 >- | P2 >
si dice che i due stati posizionali interferiscono in modo distruttivo per creare lo stato energetico ^non vincolato"..
Se riprendiamo l'analogia con il pane, lo stato d'animo della persona è un'esitazione tra l'andare a comprare il pane dal fornaio o dal pasticcere, ma anche tra l'andare a comprare il pane o non comprare il pane..
Si può dire che la determinazione ad andare a comprare il pane è una interférence_it di tutte le possibilità per andare a comprare il pane, mentre la rinuncia è una interférence_it distruttivo di questi stessi stati possibili.
Consideriamo tutte le possibilità che possono accadere al sistema e che sono tutte incluse nello spazio degli stati..
Geometricamente questo può essere rappresentato come segue:
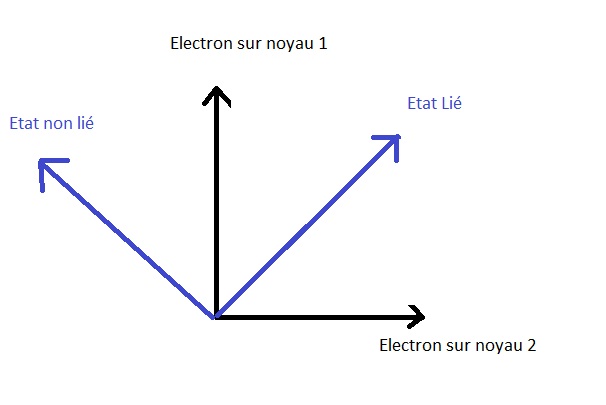
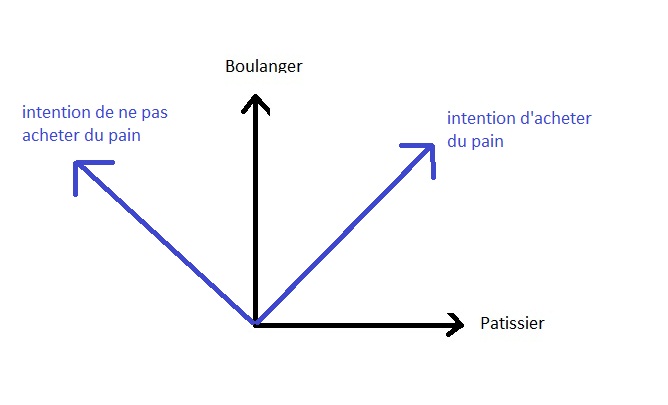Si può notare che gli stati energetici osservabili (stati legati o non legati della molecola) sono anche ortogonali perché corrispondono a possibili opzioni energetiche che sono incompatibili tra loro.
Lo stato del sistema (vettore di stato) è di per sé indipendente dalla sua rappresentazione nello spazio degli stati, sia per quanto riguarda l'energia che la posizione..
Gli autostati associati a un operatore sono detti una base per la rappresentazione del vettore stato (qui base blu o nera) Quindi, per il vettore di stato, abbiamo una base di rappresentazione per l'operatore di posizione e una base di rappresentazione diversa per l'operatore di energia.
1.1.2.Principio di inerzia di Heisenberg
Il principe_d_incertitude_de_Heisenberg segue direttamente dai postulati della meccanica quantistica.
Abbiamo visto che in generale gli autostati di due osservabili non sono rappresentati dagli stessi vettori e che uno stato energetico, ad esempio, sarà rappresentato da una combinazione lineare (sovrapposizione) di stati posizionali.
In questo caso, è chiaro che è impossibile osservare sia la proprietà della posizione che la proprietà dell'energia di un sistema durante la stessa misurazione, poiché i loro autostati sono incompatibili..
Matematicamente diciamo che gli operatori non commutano.
Ciò significa che se i due operatori vengono applicati successivamente al sistema in un ordine diverso, lo stato finale sarà diverso..
In pratica, in un esperimento quantistico, viene osservato un gran numero di particelle che danno un risultato statistico globale in cui risulta che più preciso è il valore dell'energia, meno precisa è la posizione e viceversa..
1.1.3.Rappresentazione della funzione d'onda nello spazio fisico
La differenza tra il vettore di stato e la funzione d'onda è che il vettore di stato è indipendente dallo spazio fisico, mentre la funzione d'onda non lo è, perché si propaga nello spazio fisico..
In meccanica quantistica, si dice che la funzione d'onda è una proiezione del vettore di stato nello spazio fisico..
Nell'immagine sottostante, abbiamo rappresentato l'aspetto dell'onda (funzione d'onda) di stati quantistici
visualizzare come l'onda interferisce in modo distruttivo o costruttivo per addizione o sottrazione.
Il funzionamento fondamentale di un'onda è lo stesso, sia che si tratti di un'onda quantistica, sia che si tratti di un'onda di
elettromagnetico o, ad esempio, un'onda sulla superficie di un corpo idrico (vaguelettes).
Un'onda ha sempre una depressione e un picco di oscillazione. (dell'onda) intorno a un valore medio (la superficie piatta dell'acqua).
I vantaggi si sommano (così come il meno) e i plus e i minus si sottraggono e si annullano a vicenda.
Per esempio, se la depressione di un'onda incontra il picco di un'altra onda, le due si annullano a vicenda, lasciando
la superficie piana dell'acqua nel punto di sovrapposizione.
1.1.3.1.Stati della molecola di idrogeno
Gli stati d'onda di un atomo o di una molecola corrispondono a ondes_stationnaires_it
che sono onde che non si propagano ma rimangono principalmente localizzate in una regione limitata
dello spazio, in questo caso intorno ai nuclei di idrogeno.
Il secondo postulato introduce quindi gli operatori che vengono applicati agli stati per trasformarli.
Possiamo quindi dire che il vettore di stato rappresenta l'aspetto statico della realtà quantistica, mentre l'operatore rappresenta l'aspetto dinamico di questa stessa realtà ..
Il terzo, il quarto e il quinto postulato descrivono il processo stesso di osservazione di un sistema quantistico..
Postulat_III
Misura : I valori possibili di un'osservabile " La misura di una grandezza fisica A può dare solo un autovalore dell'osservabile A corrispondente tra tutti i valori possibili..
" Abbiamo visto che gli stati osservabili di una proprietà di un sistema quantistico sono chiamati "stati indigeni". (di questa osservabile).
Ogni ^stato di autovalori" ha un ^valore di autovalori" associato, che è il risultato della misurazione..
Ad esempio, per la molecola di idrogeno sarà il livello energetico della molecola ad essere diverso se la molecola si trova nello stato legato o non legato..
Nell'analogia del pane, si può immaginare che il risultato sia la variazione della quantità di denaro nel borsellino che è diminuita quando il pane è stato acquistato..
L'autovalore è un numero, mentre l'autostato è, come abbiamo visto, un vettore..
Finora abbiamo utilizzato solo la direzione del vettore, che è anche associata a una dimensione dello spazio di stato, poiché questa è la nozione più importante relativa allo stato quantistico..
In matematica il valore naturale associato ad un vettore è la sua lunghezza.
Questa lunghezza è astratta (non è uno spazio fisico e quindi non si misura in metri).
Per questo motivo è stato creato un termine più generale che si riferisce alla lunghezza o alla scala, da cui il nome ^valore scalare"..
Lo scalare è quindi il valore numerico associato alla lunghezza di un vettore.
Se moltiplichiamo la lunghezza di un vettore per un numero otterremo un vettore la cui lunghezza è un multiplo del valore iniziale, sarà in una scala diversa, il suo nuovo valore "scalare"..
Osserviamo quindi l'energia del sistema utilizzando l'operatore energetico.
Abbiamo visto che in questo caso l'applicazione dell'operatore energetico sullo stato dà i due possibili stati energetici contemporaneamente:
H applicato al | stato > darà lo stato | Il > (al link) associato all'energia El è lo stato | Enl > (per i non correlati) associato all'energia Enl (le energie sono gli autovalori dell'operatore di energia).
L'operatore logico "o" (o non esclusivo) è rappresentato in meccanica quantistica nello spazio degli stati dall'addizione dei vettori noti " ".
Abbiamo quindi:
H | stato > = Il | Il > Enl | Enl >
Lo stato globale è una sovrapposizione dei possibili autostati dove El ed Enl rappresentano, come abbiamo visto, i valori energetici dei due stati rispettivamente.
Per rappresentare il fatto che durante una misurazione è possibile ottenere un solo valore, si utilizza una proprietà dei vettori chiamata proiezione..
Di seguito è riportata l'immagine della proiezione di stato globale |Psy> sullo stato energetico della molecola legata | Il >
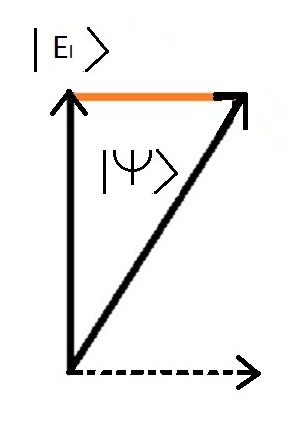Quando la proprietà fisica viene misurata sul sistema, il postulato è che la misurazione fornisca un valore unico e che questo valore corrisponda a un particolare stato del sistema chiamato ^stato di autovalore^, il valore ottenuto viene chiamato ^valore di autovalore^..
Nell'equazione precedente si aggiungono possibilità e non valori, quindi non si ha E = El Enl, l'aggiunta di un vettore non funziona come l'aggiunta di un valore (scalare).
Vedremo in seguito che sommando le possibilità non si otterrà la somma delle energie, ma il valore medio dell'energia che è la somma dei valori (ici El Enl) diviso per il numero di valori aggiunti (ici 2).
Il valore medio dell'energia sarebbe quindi E = (El Enl)/2.
In realtà è un po' più sottile di così, perché il valore medio dell'energia dipende anche dalla probabilità di esistenza di ogni stato di energia, quindi è un valore medio ponderato per la probabilità di ogni stato..
È proprio questo l'oggetto del quarto postulato.
Postulat_IV
Postulato di nascita : interpretazione probabilistica della funzione d'onda "Quando si misura la grandezza fisica A su un sistema nello stato normalizzato "phi", la probabilità P (Un) per ottenere l'autovalore An dell'osservabile A corrispondente è |Cn|².
Dove Cn è l'ampiezza della funzione d'onda proiettata sull'autostato |phi n> corrispondente all'autovalore osservato An.
Finora abbiamo parlato solo di stati, autostati osservabili e autovalori associati..
Per convenzione, la lunghezza di qualsiasi vettore di stato è 1, perché il vettore di stato trasmette l'esistenza del sistema. (prima ipotesi) e che, in termini di probabilità , l'affermazione dell'esistenza del sistema corrisponde a una certezza.
In probabilità la certezza è 1.
Quando si ha una possibilità su 1 di ottenere qualcosa (1 diviso 1 è uguale a 1) siamo nella certezza.
Una probabilità inferiore a 1 è meno certa di una piena certezza..
Ad esempio, la possibilità di vincere alla lotteria giocando una sola griglia è pari a 1 diviso per qualche milione..
Ciò significa che alla fine solo uno o quasi uno vincerà i milioni dell'estrazione. ! Il sorteggio in termini quantistici è ^l'osservazione del vincitore"..
L'ampiezza della funzione d'onda è uguale alla lunghezza del vettore di stato.
Abbiamo visto che uno scalare è un semplice valore numerico.
Questa denominazione compare anche rispetto a valori numerici più complessi composti da più numeri, come il vettore che, se rappresentato numericamente, richiede l'uso di più numeri.
(se seguiamo questa linea di sviluppo arriviamo al concetto di ^tensore" molto utilizzato in fisica, tensore dell'elasticità , della curvatura dello spazio-tempo...Postulato IV nweb).
_
Quando si proietta un vettore su un altro, la lunghezza trasportata dal primo al secondo è un numero.
Abbiamo così effettuato un'operazione che associa un numero a due vettori, che chiamiamo scalare per indicare che il risultato particolare di questa operazione di due vettori non dà un terzo vettore come nell'addizione di vettori ma un numero (scalare).
Questa operazione è chiamata prodotto scalare: Il prodotto scalare è un'operazione che, a partire da due vettori, dà un numero.
Questo numero è la lunghezza proiettata ortogonalmente di un vettore sull'altro..
La parola inglese "bracket" si riferisce ai caratteri "<" et ">Queste parentesi sono tradizionalmente utilizzate in matematica per rappresentare il valore medio di una quantità .. L'immagine sottostante rappresenta la proiezione dello stato generale | Cani > sui due stati energetici | Cani l > e | Cani nl > (che sono gli stessi degli stati | Il > e | Enl > è solo una differenza di notazione)
Quando abbiamo considerato gli stati " comprare pane" |fornaio> e |fornaio> abbiamo implicitamente ritenuto di poter osservare l'uno e l'altro in modo indifferente, cioè con un'uguale probabilità di verificarsi.
La somma dei quadrati delle lunghezze dei due lati è uguale al quadrato della lunghezza dell'ipotenusa. Nel nostro caso l'ipotenusa corrisponde al vettore di stato |phi> ed entrambi i lati al |phi> sui due autostati |fornaio> e | Epicier>.
1.2.1.Operatore dell'evoluzione
Se consideriamo l'espressione | Cani L >< Cani L | composto da un ket e da un reggiseno e applicato al ket | Cani > otteniamo | Cani L >< Cani L | Cani > dove < Cani L | Cani > è l'ampiezza di probabilità di ottenere lo stato | Cani L > quindi abbiamo : | Cani L >< Cani L | Cani > = | Cani L > Al = Al | Cani L > vediamo che lo stato finale è il | Cani L > associato alla probabilità Al L'espressione | Cani L >< Cani L | è quindi un operatore che ha modificato lo stato iniziale | Cani > allo stato finale | Cani L > e questo con una probabilità Al.
1.2.2.Partizione dell'operatore dell'unitÃ
Si consideri il seguente operatore:
| Cani L >< Cani L | | Cani nl >< Cani nl | che è la somma degli operatori di evoluzione verso gli autostati di un'osservabile (qui l'energia : stato vincolato e non vincolato).
È interessante notare come la rappresentazione vettoriale dello stato e la sua decomposizione secondo una base ortogonale permetta di rappresentare in modo naturale le ampiezze delle probabilità e quindi le probabilità dell'evoluzione del sistema durante una misurazione..
Postulat_V
Misura : riduzione del pacchetto d'onda Se la misura della grandezza fisica A, al tempo t, su un sistema rappresentato dal vettore |phi> risulta l'autovalore An, allora lo stato del sistema subito dopo la misurazione viene proiettato sull'autospazio associato ad An Questo postulato è anche chiamato ^postulato di riduzione dei pacchetti di onde"..
È probabilmente la più grande rivoluzione concettuale della meccanica quantistica l'introduzione del fatto che l'osservazione del sistema ne provoca l'evoluzione, mentre nelle teorie fisiche non quantistiche è solo l'equazione dinamica a essere responsabile dell'evoluzione del sistema.
Tradizionalmente l'equazione dinamica di una teoria meccanica esprime come l'energia agisce sul sistema per trasformarlo.
L_expérience_du_chat_de_Shroedinger è un esperimento di pensiero ideato dal fisico Erwin_Shroedinger riflettere sul problema della misurazione in meccanica quantistica direttamente collegato al quinto postulato.
Si noti il legame tra l'osservatore e la funzione d'onda: nessuno dei quali è materiale ! Si potrebbe dire che ciò che è materiale è ciò che sta tra i due: osservazione.
La funzione d'onda e la coscienza rappresentano due facce di una stessa realtà che trascende la materialità e la
all'origine di questa materialità .
Ovviamente i fisici nel loro complesso non si spingono così lontano nella loro visione della realtà quantistica..
La posizione standard in quest'area è lainterprétation_de_l_école_de_Copenhague.
Questa posizione emerge dalla situazione dell'osservatore umano che sperimenta un mondo classico e lo considera come riferimento assoluto..
Si possono definire diversi gradi di distanza da questa posizione:
Va notato che questo punto di vista non è più scientificamente sostenibile da quando l'esperimento di Aspect, che ha convalidato la meccanica, è stato approvato.
Allo stesso tempo, la meccanica quantistica è la teoria più verificata nella storia della scienza..
Questo punto di vista si riduce quindi a una semplice credenza ^materialista^..
Questo era tuttavia il punto di vista di Einstein, che purtroppo non è vissuto abbastanza a lungo per
vedere la risoluzione, tramite l'esperimento Aspect, del paradosso che aveva definito con i fisici Podolsky e Rosen nel suo celebre articolo:
il Paradoxe_EPR.
In questo caso il mondo classico in cui viviamo non rappresenta più la totalità del mondo perché ci sono
un mondo quantistico assolutamente strano al quale non abbiamo accesso ma con il quale possiamo confrontarci con
attraverso la teoria quantistica.
Il mondo fisico stabile che conosciamo è costituito solo da tre particelle quantistiche: elettrone, protone e neutrino.
Questo terzo punto di vista elimina tutti i paradossi quantistici affermando, infine e semplicemente, che non bisogna
non cercare un'interpretazione (classico) della teoria quantistica, ma che si deve semplicemente accettare
come è (Copenaghen) e finalmente riconoscere la supremazia della sua posizione.
Si può quindi prevedere che il modello quantistico non sarà mai messo in discussione.. Fin dalla sua nascita, è diventato sempre più chiaro come la realtà quantistica
interviene nella comprensione del mondo che ci circonda e più in particolare nel campo della vita, un sistema macroscopico di grande coerenza... quantistico.
Due esempi abbastanza recenti sono:
Postulat_VI evoluzione temporale dello stato quantistico. _ H |Phi(t)> = i h/2*pi d |Phi(t)> / dt _
0,000000000000000000000000000000000662607004 Quando questa costante viene combinata con altre costanti fondamentali come la velocità della luce o la costante di gravitazione universale, si possono dedurre le quantità minime delle diverse unità della fisica : Lunghezza di Planck, tempo di Planck, ecc....
1.5.Espressione poetica condensata di postulati
Il seguente è un tentativo di combinare tutti gli assunti in un unico aforisma:
Ciò che è possibile si compie, sotto l'occhio della coscienza si compie solo ciò che è possibile..
La meccanica quantistica è la più grande rivoluzione della nostra era scientifica moderna perché distrugge definitivamente la posizione materialista, aprendo così la strada a uno sviluppo dell'umanità in cui scienza e coscienza saranno di nuovo unite.
L'esperimento decisivo che ha risolto la parodia Einstein-Podolski-Rosen
realizzato nel 1982 da Alain Aspect, ricercatore e sperimentatore presso il centro di ottica quantistica di Orsay
era basato sui fotoni.
Una descrizione dettagliata della teoria sottostante si trova nel libro
di Bernard d'Espagnat ^A la recherche du réel".
Nello stesso anno, ero all'università e Alain Aspect è venuto a presentare
i suoi risultati a Tolosa, nell'anfiteatro Maxwell dell'Università Paul Sabatier.
Dopo aver presentato i risultati inequivocabili delle misurazioni, ha lasciato
l'assemblea senza voce (l'aula magna era gremita di professori e ricercatori).
Al termine della presentazione, dopo un significativo momento di silenzio, quando è stata aperta la parola, l'oratore ha detto
è stato dato all'assemblea, solo un ricercatore si è alzato in piedi (il mio insegnante di relatività ) e ha posto questa domanda:
E per te è facile convivere con questo?.
Aspect, sulla difensiva, rispose che non aveva detto questo, che aveva fatto
un esperimento e che il risultato è stato quello, ma che ha fatto attenzione a non
dare qualsiasi interpretazione.
Anni dopo ho appreso da una persona che era stata con lui che era
pro-Einsteina e che si aspettava che la meccanica quantistica venisse messa in discussione.
Ero in terza fila, nell'area laterale, tutto solo, e mi divertivo perché non capivo
perché avevano un problema, o meglio lo capivo fin troppo bene..
Quando l'esperimento era agli inizi, il risultato era solo una questione di tempo,
la polemica è diventata molto forte, addirittura sulfurea.
Quando la comunità scientifica dei fisici era in stato di shock, noi
si chiedeva cosa sarebbe successo.
C'è voluto del tempo per far digerire le informazioni, ma nel 2020 possiamo vedere che la situazione
si è evoluto parecchio, basta dare un'occhiata a questa conferenza tenuta all'Ecole Polytechnique
di Hervé Zwirn, direttore della ricerca del CNRS
_x_sciences_de_l_homme_et_de_la_société_x_shs_mécanique_quantique_le_monde_existe_t_il
Questa esperienza ha (o che avrebbe dovuto avere per la maggioranza) lo stesso tipo di effetto nel
fisici che la scoperta delle onde radio (onde elettromagnetiche) che hanno
dare al concetto astratto di campo elettromagnetico una realtà molto più vivida.
La scoperta della non-separabilità e la sua osservazione nella
livello fisico dà vita al concetto di realtà indipendente, vale a dire
di una realtà indipendente dallo spazio e dal tempo, cioè da tutte le
le contingenze spazio-temporali, cioè tutte le contingenze fisiche.
Una prima conclusione che si può trarre dal primo postulato della meccanica
è che:
La realtà di un sistema quantistico (e alla fine, tutti i sistemi sono quantistici! x scienze umane e sociali x shs meccanica quantistica il mondo esiste nwebs) è sostenuta da
da uno spazio astratto di possibilità che non è osservabile di per sé (non fisico e
indipendente da tutte le contingenze spazio-temporali) ma comunque reale, poiché è
Da questo livello astratto di funzionamento emerge la realtà concreta. (osservato).
Per riassumere in una parola: è l'onnipresenza e l'onniscienza poiché contiene
tutte le informazioni sul sistema fisico in modo non locale.
Inoltre, per completezza, questo è legato all'osservatore, che ovviamente non può essere fisico..
Risulta evidente che l'osservatore e la realtà indipendente hanno una stretta relazione:
sono entrambi non fisici e interagiscono in termini di informazione, conoscenza, percezione.
In questo senso, il film Matrix può essere visto come un'allegoria della realtà quantistica..
A questa coscienza universale si può dare e si è dato il nome che si vuole.
Il valore medio dell'energia sarà notato, ad esempio < E >.
Abbiamo visto che lo stato quantistico è chiamato anche "ket" notato | ket > l'altra parte della parentesi è la "bra" che è un operatore particolare notato < reggiseno | È il fisico Paul_Dirac che è all'origine di questa separazione in due di questa parola per far apparire una dinamica di operatore e vettore nell'operazione di assunzione del valore medio.
Se applichiamo la ^bra^ al ^ket^ otteniamo < reggiseno | ket > che è il numero che risulta dall'applicazione dell'operatore
Qui abbiamo una duplice relazione tra reggiseno e ket.
Per uno Stato (ou ket) "| Cani >" le bra sera "< Cani |La dualità tra i due è rappresentata come l'immagine in uno specchio Il ket è un vettore mentre il bra è un operatore, applicando il bra al ket si ottiene un numero..
In generale, in un'espressione, ciò che si trova a destra del ket è un operatore, il risultato di un operatore su uno stato (vettore) è un altro stato (vettore) un numero che rappresenta il risultato di una misurazione o una probabilità .
Per ogni ket c'è un reggiseno corrispondente e l'operazione che permette di passare dal ket al reggiseno si chiama coniugazione ermetica ed è segnalata da una stella.
Così ( | Cani > ) * = < Cani | o (
Ciò può essere analogamente collegato a un aforisma vedico in cui il creatore dell'universo parla: Mi sono ripiegato su me stesso e ho creato ancora e ancora..
La stessa forma si ritrova anche nel primo racconto della creazione, nella Genesi.: sia la luce e ci fu la luce e D.
Dio vide che la luce era buona.
< che ci sia luce | e la luce era > = e D.
Dio vide che la luce era buona.
< o | luce². | barile > = D.
Dio vide che la luce era buona.
Il fatto che D.
Dio vide che la luce era buona è chiaramente il risultato di un'osservazione.
Potremmo chiamare tutto questo alfabeto quantistico e sintassi.
L'alfabeto è composto da una sola lettera | Cani > e questo è l'essere... (o lo stato che è l'affermazione dell'essere) La doppia operazione * mostra il suo valore di operatore dinamico ( | Cani > )* = < Cani | Tutte le loro combinazioni danno luogo alla grammatica quantistica.
Un esempio è l'applicazione dell'operatore < Cani | sullo stato | Cani > dà < Psy|Cani > che è anche la proiezione del |Psy> su se stesso ed è quindi 1.
Questo può essere banalmente tradotto nella seguente frase: Psy partecipa al 100%. (100/100=1) a Psy".
< Cani L | Cani > è la proiezione dello stato generale del sistema sullo stato energetico vincolato dell'esempio della molecola H2 e rappresenta l'ampiezza della probabilità di ottenere lo stato vincolato durante un'osservazione.
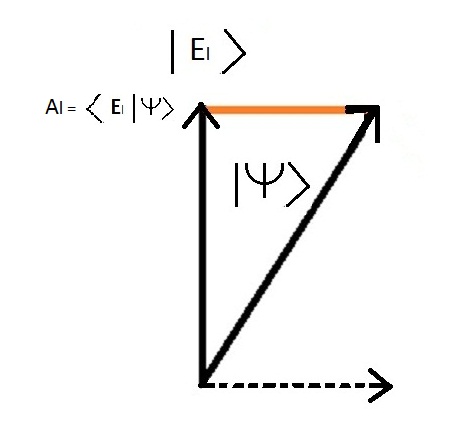
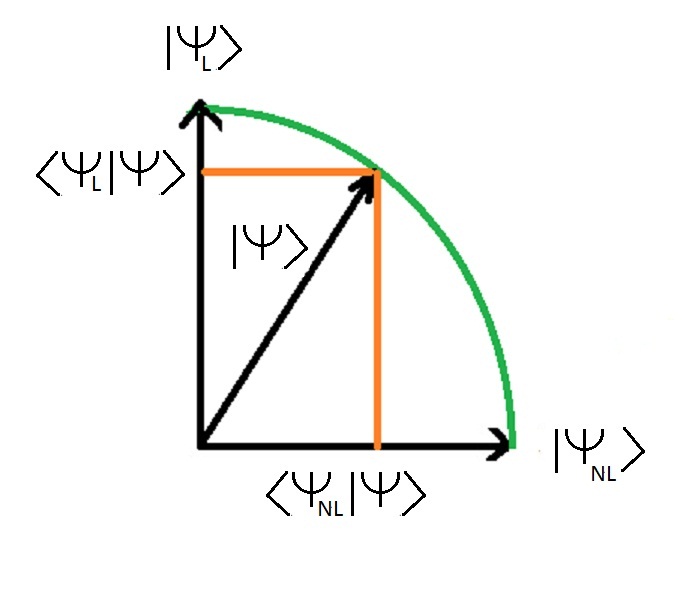Al = < Cani L | Cani > Prendendo il quadrato dell'ampiezza si ottiene la probabilità La probabilità dello stato | Cani L > è: Pl = Al² = ( < Cani L | Cani > )² 
I due valori < Cani l | Cani > e < Cani nl | Cani > sono la lunghezza dello stato | Cani > (che è 1) proiettato sulle proprie dichiarazioni | Cani l > e | Cani nl > < Cani l | Cani > è la proiezione dello stato | Cani > sullo stato pulito | Cani l > < Cani nl | Cani > è la proiezione dello stato | Cani > sullo stato pulito | Cani nl >
Questo è noto come stato equiprobabile.
Ma le caratteristiche del sistema possono essere tali da non farlo, ad esempio se il panettiere è più vicino a casa del pasticciere e fa molto freddo la probabilità dello stato |fornaio> sarà più forte di quello dello Stato |fornaio>.
Questo è rappresentato nell'immagine sottostante, dove Ab è maggiore di Ap.
(A è l'ampiezza di probabilità ).
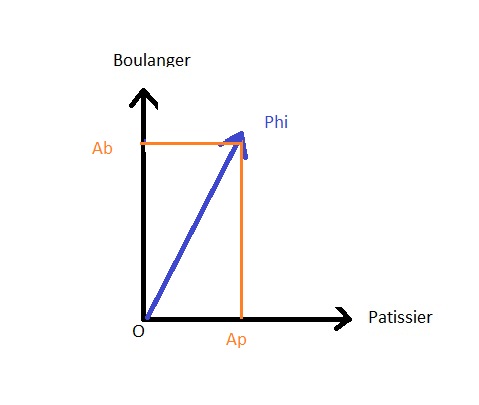La proiezione dello Stato |Phi> generale sullo Stato |fornaio> ha il valore Ab che corrisponde all'ampiezza della probabilità di ottenere questo stato dallo stato generale |Phi> Lo stesso vale per Ap che è l'ampiezza della probabilità di ottenere lo stato |fornaio>.
Gli autostati quantistici sono sempre ortogonali, cioè si trovano ad angolo retto l'uno rispetto all'altro e quindi seguono la . Pythagore
per il triangolo rettangolo.
Il postulato dice che il quadrato dell'ampiezza dell'onda rappresenta la probabilità .
Considerare lo stato generale del sistema significa semplicemente considerare che c'è: la probabilità dello stato effettivo del sistema è quindi sempre uguale a 1.
Questo è ciò che il postulato menziona affermando che lo stato |phi> è normato e la sua norma è sempre uguale a 1 per convenzione, poiché è una probabilità .
Matematicamente notiamo < phi | phi > = 1 = | |phi> | ² (l'ultima espressione rappresenta il quadrato della norma del vettore, essendo la norma del vettore la sua lunghezza) Questa probabilità viene poi suddivisa in diverse probabilità inferiori corrispondenti a ciascun autostato, ma con il vincolo che la somma dei quadrati delle ampiezze degli autostati del sistema sia sempre uguale a 1, che è la probabilità certa.
Nel nostro caso abbiamo:
Ab² Ap² = 1 La somma delle probabilità di tutti gli stati possibili del sistema deve essere uguale a 1.
Si può dire che l'esistenza del sistema è distribuita su tutte le sue possibilità di esistenza, ma senza alcuna perdita di esistenza, in modo da preservare la sua esistenza..
Infatti, se la probabilità totale diminuisse, ciò significherebbe che il sistema avrebbe meno possibilità di esistere e, riducendo a zero la probabilità della sua esistenza, scomparirebbe. ! L'ampiezza dello stato o della funzione d'onda può essere positiva o negativa, proprio come il picco o la depressione di un'onda..
L'ampiezza della probabilità è quindi negativa o positiva, il che è ciò che abbiamo rappresentato nell'immagine degli stati legati e non legati della molecola di idrogeno con i simboli più e meno -. .
(. états molécule hydrogène Pitagorico) Ma la probabilità che è il quadrato dell'ampiezza (o il quadrato dello standard ) è quindi sempre positivo, il che è normale per una probabilità .
Infatti, possiamo immaginare una probabilità certa, poi una meno certa, poi una incerta o addirittura una nulla, ma una probabilità negativa è priva di significato..
D'altra parte, l'ampiezza della probabilità può essere negativa.
Supponiamo poi di avere due ampiezze di probabilità uguali ma di segno opposto che si propagano l'una verso l'altra (sono onde).
Se consideriamo le probabilità quando queste ampiezze si trovano nello stesso punto, allora le ampiezze di segno opposto si annullano e anche il loro quadrato è pari a zero.
La probabilità di osservare qualcosa sarà pari a zero.
Ma se le ampiezze sono separate, il loro quadrato sarà positivo. (il più per il più è positivo, ma anche il meno per il meno è positivo) e quindi la probabilità di osservare qualcosa non sarà più pari a zero.
Quando si parla di meccanica quantistica si pensa al suo carattere probabilistico come a un gioco d'azzardo, ma ciò che generalmente si ignora è che queste probabilità sono sostenute da qualcosa di molto più inquietante, che è l'ampiezza dell'onda di probabilità e che dà alla meccanica quantistica la sua realtà .
È un operatore di evoluzione che ha fatto evolvere il sistema verso lo stato di energia vincolata durante un'osservazione..
Questo ci porta naturalmente al quinto postulato, che descrive l'evoluzione del sistema durante la misurazione..
Se applichiamo questo operatore a ket | Cani > su un :
( | Cani L >< Cani L | | Cani nl >< Cani nl | ) | Cani > o | Cani L >< Cani L | Cani > | Cani nl >< Cani nl | Cani > che si traduce in | Cani L > Al | Cani nl > Anl o anche Al | Cani L > Anl | Cani nl > che è la decomposizione dello stato | Cani > nella somma dei propri stati energetici | Cani > = Al | Cani L > Anl | Cani nl > L'operatore non ha modificato lo stato | Cani > ma l'ha semplicemente scomposta nelle sue singole parti, per questo motivo è chiamato operatore di ^partizione unitaria"..
Prima di tutto, chiariamo la nozione di ^sottospazio-eigeni"..
Si tratta solo di una generalizzazione della scomposizione dello stato nei suoi autostati.
Torniamo all'esempio del pane con due panettieri e un pasticcere.
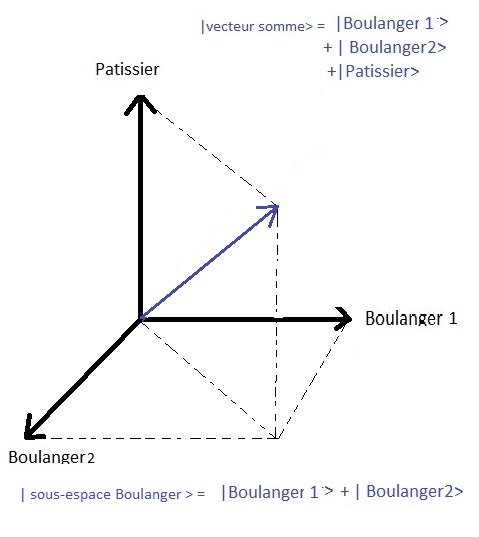
Se la distinzione della tipologia di commercio non è osservabile (non è un'osservabile del sistema)Nel caso di una misurazione, non sarà necessario distinguere se si tratta del panettiere 1 o del panettiere 2, sarà sufficiente sapere che lo stato è stato proiettato nel sottospazio proprio del panettiere, che di fatto corrisponde, nel diagramma sottostante, al piano orizzontale popolato dai panettieri ! Se ci fosse un osservabile che ci permettesse di osservare da quale panettiere è stato comprato il pane, durante questa misurazione lo stato verrebbe proiettato su uno o l'altro panettiere, eliminando l'indeterminatezza della misurazione..
Ma se questa proprietà del sistema non viene osservata, il sistema rimane in questo stato di sovrapposizione delle funzioni d'onda di Baker..
Lo stato è detto degenerato.
In pratica, quando più autostati hanno lo stesso autovalore (stessa energia) hanno detto che questi stati sono degenerati.
Applicando un ulteriore vincolo energetico al sistema che modificherà l'energia degli stati degenerati in modo che non vi sia più uguaglianza, la degenerazione verrà rimossa..
La fisica quantistica si occupa essenzialmente di comprendere la struttura del mondo microscopico che è essenzialmente costituito da risonanze (onde stazionarie) che sono autostati dell'operatore di energia totale del sistema (Hamiltonien).
Il quinto postulato afferma che durante la misurazione lo stato del sistema evolve verso lo stato il cui autovalore è stato misurato..
È questo cosiddetto postulato della ^riduzione del pacchetto d'onda^ o ^collasso della funzione d'onda" che dà alla rappresentazione geometrica di una proiezione vettoriale la sua realtà fisica, poiché il sistema si evolve fisicamente in questa operazione.
In questo quinto postulato abbiamo visto che la misurazione stessa trasforma il sistema.
Anche nel caso della meccanica quantistica esiste un'equazione dinamica di questo tipo, denominata l'equazione di Shroedinger .
In meccanica, ci sono quindi due meccanismi per l'evoluzione: l'azione dell'energia nel tempo e l'azione dell'osservazione fuori dal tempo.
Questa equazione costituisce il sesto e ultimo postulato della meccanica quantistica. (vedi sotto).
Il quinto postulato coinvolge l'osservatore del sistema nell'evoluzione del sistema stesso..
Nella meccanica quantistica, quindi, l'osservatore non è più indipendente dal sistema fisico..
L'osservatore e il sistema fisico formano un tutt'uno inscindibile.
Si potrebbe dire che l'osservatore è incorporato nel sistema (ma non nel senso dell'entanglement quantistico, che riguarda soltanto la funzione d'onda).
Abbiamo già accennato al fenomeno dell'entanglement quantistico, che nasce dal fatto che un sistema quantistico composto da più particelle è descritto da un'unica funzione d'onda (prima ipotesi) anche se è probabile che le particelle si siano allontanate nello spazio fisico.
Secondo il quinto postulato, durante una misurazione la funzione d'onda collassa in un proprio sottospazio influenzando istantaneamente lo stato di tutte le particelle che compongono il sistema..
È questa l'implicazione della meccanica quantistica che Einstein ufficialmente non avrebbe mai potuto ammettere perché, a suo avviso, violava il limite di propagazione di qualsiasi interazione fisica definito dalla velocità della luce..
Secondo la teoria della relatività di Einstein, nessuna energia può viaggiare più veloce della luce..
La luce viaggia ovviamente alla velocità della luce e può farlo solo perché è pura energia, cioè senza massa..
Le particelle di massa devono quindi necessariamente muoversi a una velocità inferiore a quella della luce..
La risoluzione ^fisica" di questo paradosso quantistico è stata effettuata da un esperimento noto come ilexpérience_d_Aspect.
Questo esperimento ha dimostrato in modo inconfutabile che la funzione d'onda non dipende dallo spazio fisico in cui viviamo.: la sua evoluzione durante il collasso dovuto all'osservazione avviene in qualsiasi punto dello spazio e allo stesso tempo.
L'esperimento di Aspect è stato replicato molte volte in condizioni sempre più sofisticate per spingere la meccanica quantistica ai suoi limiti, ma non ha mai ceduto. ! Si dice che la teoria quantistica sia una teoria non locale.
I termini usati ^non-località ^ o ^non-separabilità ^ sono equivalenti.
Possiamo quindi dire che la funzione d'onda quantistica trascende lo spazio fisico, anzi trascende lo spazio-tempo, poiché dalla teoria della relatività di Einstein dobbiamo considerare lo spazio e il tempo come aspetti della stessa realtà più profonda. : il continuum spazio-temporale.
Un esperimento più recente, condotto in ambito relativistico e successivo all'esperimento di Aspect, ha confermato la validità dell'entanglement quantistico in ambito relativistico.
( cf Expérience_d_Antoine_Suarez trovato sul sito web del fisico Philippe_Guillemant che offre una visione che integra la realtà quantistica ) Quest'ultimo esperimento è importante perché in un esperimento di fisica si possono misurare solo valori all'interno di un certo range.
Pertanto, nel primo esperimento Aspect, i rivelatori per fotoni correlati (in un singolo stato quantistico) erano a pochi metri l'uno dall'altro.
Ciò è bastato a dimostrare che l'entanglement quantistico non può essere dovuto a un fenomeno fisico sconosciuto. (variabile nascosta) a velocità subluminale.
La velocità di un tale fenomeno sarebbe necessariamente superluminale.
Sebbene una tale velocità superluminale sia difficilmente accettabile a causa della teoria della relatività di Einstein, il primo esperimento di Aspect non ha scartato completamente questa possibilità .
Con l'esperimento di Antoine Suarez questo avviene perché è addirittura la possibilità di una causalità tra le rilevazioni dei due fotoni correlati che viene soppressa, in quanto i quadri di riferimento relativistici in cui vengono effettuate le rilevazioni non consentono un ^prima^ e un ^dopo^, condizione essenziale per la causalità .: Nessuno dei due fotoni viene rilevato prima o dopo l'altro, perché i rilevamenti non avvengono negli stessi tempi..
In una teoria quantistica relativistica la funzione d'onda non può quindi più dipendere dal tempo come abbiamo visto nel primo postulato.
Il motivo è che il tempo è ridotto allo stesso livello della posizione, cioè a una proprietà osservabile del sistema, e la funzione d'onda è indipendente dalle proprietà del sistema. (seconda premessa).
In tale teoria la funzione d'onda sarebbe | Cani > e non più | Psy(t) > .
Il tempo sarebbe un'osservabile T allo stesso modo della posizione P.
La particolarità di questo esperimento di pensiero completamente irrealistico, presentato con un gatto ^reale^, è quella di far riflettere su cosa sia l'osservatore nella meccanica quantistica..
Nei postulati sulla misura si è visto che (o osservazione) che non entriamo nel dettaglio di ciò che l'osservatore è.
I postulati dicono che esiste un osservatore che effettua la misurazione, ma non dicono nulla di più sulla natura dell'osservatore. ! In questo esperimento, un gatto viene isolato in una scatola in modo da non poter essere osservato. (quantificato) in qualsiasi modo.
Questo presuppone che il gatto possa essere considerato come un oggetto quantistico, cosa che non avviene nella pratica, anche se in teoria il gatto può essere considerato a priori come un sistema fisico, essendo composto da atomi che sono e sono ben descritti dalla meccanica quantistica.
In questa camera si trova anche una fiala contenente un gas letale per il gatto e un rilevatore di particelle che apre la fiala se viene rilevata una particella..
Se viene rilevata una particella, il gatto è morto, se non viene rilevata, il gatto è vivo..
Finché non abbiamo osservato lo stato di salute del gatto ^quantico" esso rimane in uno stato quantistico generale noto come sovrapposizione di autostati osservabili, che sono | gatto vivo > e | chat mort > quindi abbiamo | chat > = | gatto vivo > | chat mort > Il nostro sistema quantistico è costituito da diversi componenti: il gatto, il rivelatore, la particella.
Tutti questi sottosistemi devono essere considerati anche nella definizione della funzione d'onda, quindi abbiamo: | particella > = | particella presente > | particella assente > e | sensore > = | particella di stato rilevata > | stato della particella non rilevata > La matematica associata alla meccanica quantistica mostra che il sistema globale che chiameremo ^shroedinger" è : | shroedinger > = | gatto, rivelatore, particella > = | chat> ¤ | sensore > ¤ | particella > dove ¤ è il ^prodotto tensoriale" dei vettori di stato.
Poiché si trovano nello stesso stato quantistico, si dice che questi diversi sottosistemi sono intricati..
Questo prodotto si comporta come una normale transazione di prodotto, è distributivo. : A * ( B C ) = A*B A*C In termini quantistici possiamo quindi sviluppare lo stato quantistico generale.
Cominciamo con il sistema costituito solo dal rivelatore e dalla particella.
| rivelatore, particella > = | sensore > ¤ | particella > = ( | particella di stato rilevata > | stato della particella non rilevata > ) ¤ ( | particella presente > | particella assente > ) sviluppando :
| rivelatore, particella > = | particella di stato rilevata > ¤ | particella presente >
| stato della particella non rilevata > ¤ | particella assente >
| stato della particella non rilevata > ¤ | particella presente >
| particella di stato rilevata > ¤ | particella assente >
Erwin Shroedinger nweb I primi due stati sono facilmente comprensibili, se la particella è presente è logico che venga rilevata e se non è presente non viene rilevata..
I due stati seguenti sono altamente improbabili, ma esistono comunque secondo la meccanica quantistica, per la quale tutto è solo un'ampiezza di probabilità .
Per lo Stato | shroedinger > completo sarebbe necessario sviluppare ulteriormente con gli stati del gatto, il che ci porterebbe a una funzione d'onda con otto possibili autostati, due dei quali altamente probabili e sei altamente improbabili.
I due stati probabili sono:
| chat mort > ¤ | particella di stato rilevata > ¤ | particella presente > | gatto vivo > ¤ | stato della particella non rilevata > ¤ | particella assente > Finché non abbiamo osservato il sistema, il che corrisponde ad esempio all'apertura della scatola, siamo in uno stato di sovrapposizione in cui il gatto si trova in uno stato vitale indeterminato..
Qui sta il paradosso.
Ma possiamo spingere il ragionamento più in là e questo è ciò che ha fatto il fisico Eugène_Wigner Premio Nobel per la Fisica.
Questo è il théorie_de_l_influence_de_la_conscience Egli considerò che l'occhio dell'osservatore che vede il gatto vivo o morto è anch'esso un sistema quantistico con due stati: | oeil > = | l'occhio vede il gatto morto > | l'occhio vede il gatto vivo > Gli stati della funzione d'onda completa prenderebbero quindi in considerazione gli stati ^allucinatori" in cui l'occhio vedrebbe morto, il gatto vivo...
Ma potremmo continuare a considerare la catena di misurazione fino al cervello dell'osservatore, che è anch'esso composto da atomi.
Quindi la domanda è : quando la misurazione viene effettivamente effettuata, cioè il collasso della funzione d'onda e quindi la scelta del risultato dell'esperimento: gatto vivo o morto.
Wigner dice che nulla di materiale può causare il collasso perché tutta la materialità è suscettibile di descrizione da parte della meccanica quantistica e quindi fa parte della funzione d'onda e si può benissimo considerare anche la funzione d'onda dell'universo.
Se nulla di materiale opera la misurazione, rimane solo qualcosa di immateriale che lo fa, e questo Wigner lo identifica con la coscienza, che infine identifica ciò che l'osservatore è.
Nella sua interpretazione L'osservatore è la coscienza .
Questo ci avvicina alla concezione di ^realtà indipendente^ o ^realtà velata^ introdotta dal fisico Bernard_d_Espagnat per la comprensione filosofica della meccanica quantistica.
bernard_d_espagnat_physique_quantique_et_réalité_la_réalité_c_est_quoi ;Recuperato da \" https://www.
youtube.
com/watch?v=Jd8FiWJ5v8M; Questo ci avvicina anche alla concezione vedica dell'antica India della realtà materiale, descritta come ^Maya^ o illusione dei sensi..
Questa Maya è formata dalle infinite interrelazioni tra tre elementi : richi, chanda e devatta che sono il soggetto, l'oggetto e la loro relazione, la conoscenza (spirituale: della mente) o la percezione (materiale: del materiale).
L'osservatore della coscienza e la realtà quantistica non materiale creano la realtà materiale fenomenologica.
In questo senso, il film Matrix è un'allegoria della realtà , con l'unica differenza, importante, che non sono le macchine a creare la realtà illusoria, ma la coscienza stessa..
Pertanto, la coscienza può essere definita come la relazione del soggetto con l'oggetto attraverso la percezione o la conoscenza..
Le seguenti triadi sono equivalenti:
samhita_tab_it
veda filosofia fisica quantistica
rishi soggetto osservatore conoscitore osservatore
devatta percezione (relazione soggetto/oggetto) osservazione conoscenza osservabile chandas oggetto osservato conosciuto risultato della misurazione: autovalore dell'osservabile
Questa posizione dice che tra due misure non c'è alcun oggetto e che l'unico oggetto che esiste è ^l'oggetto osservato"..
Il termine classico corrisponde a ciò che l'umanità nel suo insieme percepisce allo stesso modo. Ma questa posizione è in conflitto con
realtà quantistica, che viene quindi percepita come totalmente paradossale.
nelle sue dichiarazioni più inquietanti.
e che, in quanto tale, dovrebbe legittimamente essere il riferimento assoluto.
Il problema centrale o cardine tra la realtà quantistica e quella classica è quello della decoerenza..
La decoerenza è il passaggio da un'operazione quantistica a una classica..
Ciò significa che quando il sistema è decoertificato, è descrivibile classicamente perché l'aspetto quantistico è scomparso..
Quando si studia la meccanica quantistica, ci viene mostrato che essa si riduce alle leggi della meccanica classica quando viene considerata su scale macroscopiche.
La decoerenza è il fatto di passare dalla descrizione del sistema fisico da parte di una singola funzione d'onda a quella di un insieme separato di corpuscoli.
Quando la funzione d'onda di un insieme di particelle ^decoerge" nel collasso della misurazione, l'aspetto ondulatorio della meccanica quantistica scompare e rimane solo l'aspetto particellare..
La teoria fisica che si occupa di descrivere un grande insieme di corpuscoli è la termodinamica statistica, che ha le sue basi nella teoria quantistica attraverso le statistiche quantistiche di Böse-Einstein e Fermi-Dirac..
Questa teoria, sviluppata nel XX secolo, permette di recuperare i risultati della termodinamica macroscopica del XIX secolo a partire da considerazioni microscopiche..
La termodinamica opera nel mondo classico della decoerenza, mentre la meccanica quantistica opera nel mondo quantistico della coerenza d'onda..
La decoerenza è il passaggio dal mondo quantistico al mondo classico..
Padroneggiare la decoerenza è la sfida per produrre il computer quantistico.
Alain Aspect nella sua conferenza Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_révolution_quantique ammette a questo proposito (al 1H23mn) Se il computer quantistico può diventare un giorno una realtà , non vede alcun motivo per cui il cervello non possa diventarlo..
Così le due realtà non fisiche: la coscienza e la funzione d'onda potrebbero essere la stessa cosa..
Lo Stato . Phi
di un qualsiasi sistema quantistico non relativistico è una soluzione dell'equazione di Schrödinger dipendente dal tempo: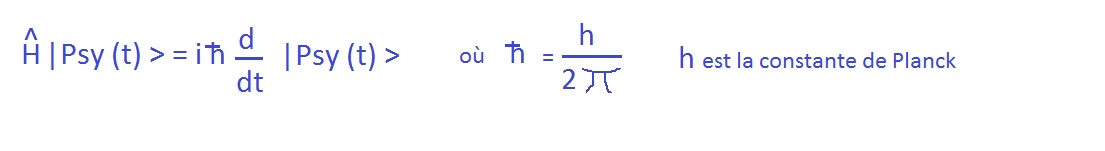 
Il sesto postulato è il. équation de Schrödinger
.
Questa è l'equazione dinamica della meccanica quantistica.
Significa semplicemente che è l'operatore \"energia totale\" del sistema, o Hamiltoniana, nota "H", che è responsabile dell'evoluzione del sistema nel tempo.
(Tradizionalmente, in meccanica quantistica, agli operatori viene dato un cappello per distinguerli da altri oggetti matematici come gli autovalori.equazione di Schrödinger) La forma dell'equazione mostra che, applicando l'operatore hamiltoniano alla funzione d'onda del sistema, si ottiene la sua derivata rispetto al tempo, cioè come varia nel tempo.
(per una variazione delta t del tempo così "dt" abbiamo una variazione "d | Psy(t) >" della funzione d'onda).
Quindi se applichiamo l'operatore hamiltoniano (energia) alla funzione d'onda otteniamo la sua evoluzione nel tempo.
È chiaro che è l'energia a far accadere le cose..
Energia e tempo sono intrinsecamente legati.
Si dice che formano una coppia di variabili coniugate.
Questa equazione è valida solo in ambito non relativistico.
In ambito relativistico l'equazione valida è l'equazione di Klein-Gordon.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf L'operatore hamiltoniano H è composto da tutte le energie che intervengono sul sistema.
Queste energie sono di due tipi: energia cinetica ed energia potenziale.
L'energia cinetica è l'energia contenuta in una massa in movimento..
Un sasso lanciato attraverso una finestra la rompe in virtù dell'energia cinetica che ha acquisito a una certa velocità ..
Se ci sono più lastre di vetro successive, maggiore è la velocità della pietra, più lastre di vetro attraverserà ..
L'energia potenziale è dovuta ai campi di forza che si applicano al sistema..
Se un sasso viene lasciato cadere su un vetro a terra, acquisterà velocità grazie all'energia potenziale gravitazionale che possiede a causa della sua distanza dalla terra..
Più passa il tempo, più l'energia potenziale si trasforma in energia cinetica e quando il sasso raggiunge il suolo, rompe la finestra in virtù dell'energia cinetica acquisita a scapito dell'energia potenziale, che ha perso..
Se lo si spinge in un pozzo, continuerà lo stesso processo fino a quando la sua energia potenziale non sarà completamente esaurita, se ciò è possibile..
Se consideriamo il movimento di un pendolo (un sasso attaccato a un supporto da una corda) quest'ultima oscilla, cioè dalla posizione iniziale (con un certo angolo rispetto alla verticale) quando il sasso viene lasciato cadere, il sasso accelera fino a quando la corda è verticale, quindi rallenta fino a fermarsi dall'altra parte in una posizione simmetrica a quella di partenza e verticale..
Il pendolo trasforma la sua energia potenziale in energia cinetica e poi la sua energia cinetica in energia potenziale, e questo ciclicamente.
Se il sistema non è sottoposto ad altre forze, il movimento non si arresta..
In pratica ci sono sempre forze di attrito che dissipano l'energia in calore fino all'esaurimento..
Ma quest'ultimo punto è vero solo nella meccanica classica, perché nella meccanica quantistica non c'è attrito. ! Un altro sistema in cui si verifica una trasformazione ciclica tra energia potenziale e cinetica è il moto di un satellite intorno a un pianeta, ad esempio la luna e la terra..
La soluzione della meccanica classica in questo caso mostra che la traiettoria del satellite è un'ellisse, vale a dire che c'è un momento in cui la luna è al massimo della sua distanza dalla terra (energia potenziale massima ed energia cinetica minima, apogeo) e un altro momento in cui la luna è più vicina alla terra (energia potenziale minima ed energia cinetica massima, perigeo).
I sistemi appena descritti sono sistemi classici, ma hanno la loro corrispondenza nel dominio quantistico.
Ad esempio, il modello del pendolo in meccanica quantistica è chiamato oscillatore armonico e il modello del satellite corrisponde al modello dell'atomo di idrogeno.: un elettrone satellite di un protone.
In meccanica quantistica, l'energia cinetica è un operatore che coinvolge la massa e l'energia potenziale è naturalmente rappresentata da un operatore la cui forma dipende dalle energie coinvolte.: potenziale elettrico e magnetico, ...
Il modo in cui la massa è coinvolta nell'equazione di Shroedinger deriva dal precedente lavoro di Louis de Broglie che stabilì la dualità onda-corpuscolo: ad ogni particella di materia possiamo associare un'onda la cui frequenza è proporzionale alla massa.
Questo si basa sulle due formule energetiche: E = m c² che è la formula dell'energia della relatività speciale di Einstein : la massa è equivalente all'energia E = h * nu che è la relazione di Planck-Einstein che spiega l'effetto fotoelettrico : l'energia è proporzionale alla frequenza.
Vediamo quindi che nell'equazione di Shroedinger è integrato un risultato della relatività speciale di Einstein.
È importante capire che le energie in gioco esercitano un vincolo sul sistema, cioè sulla funzione d'onda.
Quando si ha a che fare con sistemi oscillatori come l'oscillatore armonico (pendolino) o l'atomo di idrogeno (le satellite)L'effetto del vincolo energetico è quello di localizzare la funzione d'onda in una regione dello spazio.
Per esempio, un sistema classico non sottoposto a forze (una meteora persa nello spazio interstellare, dove le forze gravitazionali delle stelle possono essere trascurate) si muoverà in linea retta all'infinito.
L'equivalente quantistico è un'onda piana che si propaga indefinitamente, come un fotone che non è soggetto ad alcuna forza. (i fotoni sono particelle prive di massa o di carica elettrica di qualsiasi tipo e quindi non sono soggetti ad alcuna forza o energia).
Quando la funzione d'onda ha una soluzione ciclica (funzione d'onda localizzata) il tempo non ha più l'effetto di allontanare le parti del sistema l'una dall'altra all'infinito.
L'elettrone rimarrà vicino al suo nucleo, che nel caso dell'atomo di idrogeno è il protone..
Allo stesso tempo, se l'onda quantistica si propaga ciclicamente in una regione finita, si sovrappone e quindi interferisce con se stessa in modo costruttivo o distruttivo..
Risolvendo l'equazione di Shroedinger di tali sistemi, si vede che il tempo non interviene più nella forma della funzione d'onda e che è soltanto lo spazio (la posizione) che determina la forma dell'onda.
Questo è il caso di ondes_stationnaires_it che è già stato menzionato.
Ciò significa che i luoghi in cui l'interferenza è costruttiva sono sempre gli stessi in cui è distruttiva..
L'onda stazionaria è un concetto potente che ci permette di capire come un fenomeno statico possa nascere da un fenomeno dinamico..
Questo è uno degli elementi che permette l'integrazione della visione quantistica.: tutta la stabilità della materia che sperimentiamo deriva da un groviglio di onde che si muovono continuamente ma la cui risultante di interferenza è stabile.
Per l'atomo, questo dà orbite ben definite le cui forme sono fornite dalle funzioni di soluzione dell'equazione di Shroedinger, gli orbitali atomici: le nuvole sono le nuvole di probabilità di presenza dell'elettrone.
Quanto più densa è la nube, tanto maggiore è la probabilità che l'elettrone sia presente.
Rappresentazione dell'ampiezza di probabilità delle onde stazionarie (armoniche) dell'oscillatore armonico.
Si noti la somiglianza con gli stati vibrazionali (Nodi e pance vibranti) di una corda vibrante.
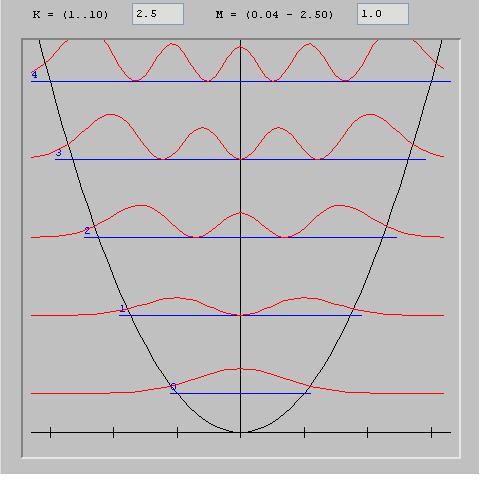
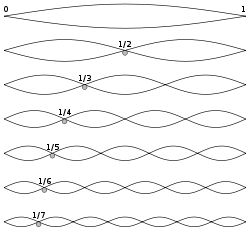Notiamo che nel caso quantistico (sinistra) l'ampiezza di probabilità delle funzioni d'onda (in rosso) diminuisce progressivamente man mano che ci si allontana dal centro, ovvero nelle regioni in cui il potenziale diventa più forte (curva parabolica in nero) ma non è mai completamente nullo.
Quindi c'è la possibilità che la particella si trovi in una regione remota dove l'energia potenziale è più alta dell'energia cinetica, mentre classicamente sarebbe intrappolata nella regione dove il potenziale è più basso della sua energia cinetica..
Questo fatto è alla base dellaeffet_tunnel che permette a una particella quantistica di attraversare una barriera di potenziale la cui energia è superiore all'energia della particella, perché la funzione d'onda non è nulla dall'altra parte della barriera, permettendo alla particella di essere osservata lì.
Questa è una conseguenza dell'aspetto non locale della funzione d'onda.
Questo è il vincolo che l'energia impone alla funzione d'onda di rimanere localizzata e quindi di interferire con se stessa per produrre onde stazionarie associate a particolari valori di energia. (Valori quantificati quindi) che è l'origine del concetto di ^quantificazione^.
Infine, è necessario parlare di ciò che è all'origine della teoria dei quanti: il constante_de_Planck che compare nell'equazione di Shroedinger.
Questa costante è stata introdotta dal fisico Max_Planck spiegare il valore della radiazione termica dalla materia in funzione della temperatura.
La legge osservata che questa radiazione segue ci costringe a considerare che l'energia termica non è emessa in modo continuo, ma in pacchetti o ^quanti"..
Si tratta della prima prova della natura quantistica della materia.
In fisica, l'azione è definita come il prodotto dell'energia e del tempo..
È abbastanza intuitivo: quando un'energia agisce per un certo tempo genera una certa azione il cui valore è proporzionale a quello dell'energia e alla durata del tempo in cui agisce.
La costante di Planck rappresenta la più piccola azione possibile nel mondo fisico..
È una costante universale della fisica che caratterizza la natura quantistica della realtà ..
Il valore di questa costante è estremamente piccolo: 6,62607004 × 10-34 m2 kg / s ma è comunque non nullo.
che sono chiamate unità di Planck.
Così il mondo fisico descritto dalla meccanica quantistica ha un limite nell'infinitamente piccolo, oltre il quale non si può più parlare in termini di fisica, ma è un limite del mondo fisico..
Se esiste un bordo, un limite, è un vincolo quantistico naturale per la funzione d'onda e quindi per la quantizzazione. (che è di per sé, come abbiamo visto, una forza).
La costante di Planck definisce la pixelatura dell'Universo.
L'origine più fondamentale della quantificazione si trova anche nel funzionamento della coscienza, che per natura non è continua..
Infatti, se consideriamo l'osservazione da parte di un soggetto di un oggetto che è un punto di vista nella coscienza, questa è possibile solo attraverso la discriminazione della coscienza di diversi punti di vista possibili..
Per essere identificati, i punti di vista devono essere distinti, altrimenti tutti i punti di vista si fonderebbero e non ci sarebbe una vera osservazione..
La discriminazione è una qualità dell'intelletto che, in questo senso, è una proprietà fondamentale della coscienza..
Troviamo quindi gli elementi presenti nei postulati quantistici della misurazione.
"
1.5.1.Analisi dell'aforisma
poesia corrispondenza quantistica link ai postulati
Che cosa è la funzione d'onda o il vettore di stato o "ket" (da staffa , gancio in francese) . Premier postulat
possibile la struttura probabilistica della funzione d'onda, le diverse possibilità di autostati del ket . Troisième postulat è realizzato la dinamica dell'operatore hamiltoniano l'energia totale del sistema responsabile dell'evoluzione. . Deuxième postulat sotto l'occhio della coscienza i postulati della misurazione, cioè il necessario intervento dell'osservatore . Quatrième postulat si realizza solo ciò che è possibile si possono ottenere solo gli autovalori dell'osservabile e lo stato del sistema è quindi il corrispondente autostato. . Cinquième postulat Ciò che è possibile è realizzato l'equazione di Schrödinger, l'equazione della dinamica quantistica. . Sixième postulat
La grande difficoltà degli scienziati ad accettare il messaggio della teoria quantistica spiega perché così poche persone riescono ad accedervi..
Qui trovate una sintesi di questa situazione, analizzata da Jean Staune e riportata da Bruno Lussato: bruno_lussato_les_plus_grandes_désinformations_de_l_histoire_des_sciences
(blog dove, nel 2009, ho lasciato un resoconto della conferenza che Alain Aspect tenne nel 1982 a Tolosa, mentre girava per le università francesi per presentare i risultati del suo lavoro.bruno lussato la più grande disinformazione della storia della scienza nweb) Questo testo avrebbe potuto essere scritto e probabilmente molto meglio da un gran numero di persone competenti che fanno parte del ^establishment scientifico^, ma la loro riluttanza a farlo mi ha portato, da un lato, a poter riservare il nome del dominio quantum.
org che era curiosamente disponibile e dall'altro lato di spendere decine di ore per elaborare questo testo che probabilmente è ancora da migliorare...
I postulati non includono ovviamente l'osservatore nel sistema fisico.
ma dichiara la sua esistenza necessaria perché un'osservazione abbia luogo o perché una
viene prodotto un risultato fisico.
Ciò si adatta perfettamente alla concezione degli sciamani del ^sogno del mondo"..
La differenza con la realtà è che la simulazione olografica del mondo non è fabbricata.
da computer materiali ma da un computer cosmico non materiale che si identifica
alla coscienza nella sua concezione più ampia.
ma non esauriranno mai l'infinito potere di questa coscienza..