The postulates of quantum mechanics
version available in : it ru zh es ja de nl pt fr
date of creation : 20240129- date of update : 20221007- generation date : 20241110_231431
This article presents in detail the postulats_de_la_mécanique_quantique from simple mathematical and geometrical considerations and analogies taken from everyday life.
In physics, concepts related to mathematical objects are developed to establish theories that allow the physical world to be represented through its laws of operation.
The classical mechanics or Newton's theory is the theory that allows to represent the functioning of matter at scales sensitive to human perception that we call macroscopic.
At cosmological scales this theory is generalized through the relativistic theories of Einstein.
General relativity is the theory that deals most completely with the gravitational force.
Quantum mechanics is the theory that allows to represent the functioning of matter at the microscopic level although the limit between the microscopic and the macroscopic is not clearly defined in terms of scale of magnitude so that we can have quantum behaviors at macroscopic scales as in the laser or the cables_électriques_supraconducteurs Quantum theory does not deal with a particular force of nature like general relativity, it is more a language.
The language of quantum objects.
Thus one will be able to apply this language to various forces or systems, one thus carries out their quantification.
The game of quantum concepts is based on six basic postulates that completely define the quantum theory.nweb superconducting electric cables We will present these six postulates and try to identify their meaning in a simple way.
The expression of the first postulate as defined in the book " Quantum Mechanics Volume 1" by Cohen-Tanoudji is :
" At a fixed time t, the state of a physical system is defined by the data
of a ket or wave function or state vector noted |psy(t)> belonging to the state space".
Postulate I nweb
The Greek letter Psy is used to designate the wave function, we use
also indifferently the letter Phy.
The first concept of mechanics concerns the representation of the state of the physical system.
This is a natural way to define the object of the study. Here we simply say that the system exists
and that we can represent its state by a function that depends on time
this is because the state of the system is not a priori static but dynamic.
In classical mechanics the physical system is represented by the "material point".
A complex system will be represented by a set of material points connected
between them to form a solid or non-solid object (rigid or non-rigid connections, for example: crystal or gas).
The first postulate simply states that the state of the system at a given time is unique
and belongs to a set of possible states grouped in a set
mathematics called "state space".
We speak of space and not simply of set because the quantum state is a vector
which is a mathematical object that represents a direction in a space.
We all know the three-dimensional space (length, width, height or depth depending on the orientation of the first two dimensions)
It is the physical space in which we live.
The space of states in which quantum systems "live" is not a physical space, it is an abstract space (Hilbert space)
and its dimension is infinite to represent the infinity of possible states that exist even for simple physical systems.
We will make an analogy with an example of everyday life
to understand how a quantum system is modeled.
Let's imagine a quiet person in his apartment who suddenly
realizes that she has to go out to buy bread.
She prepares to leave and in her mind she still hesitates about the place where she will go to buy bread.
She has a choice between a bakery further up the street or a pastry shop that also makes
and who is further down the street from her.
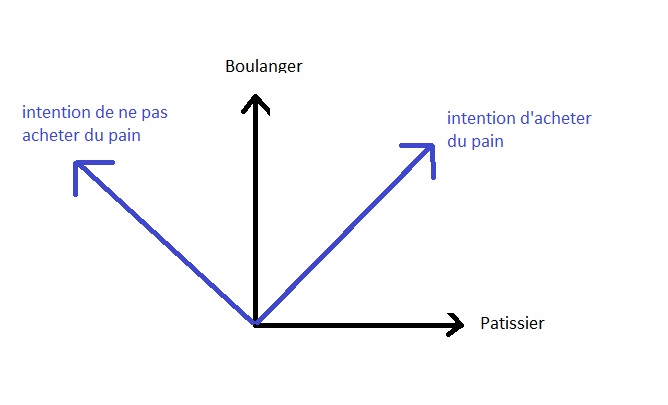
Going down the stairs to leave we can say that there are two states possible in his mind that correspond to the two options for buy bread. We can note these options in the quantum way:
state 1: |baker>
status 2: |pastry shop>
The person's state of mind is a combination of these two possibilities:
| State> = |baker> + |pastry shop>
The two states are completely incompatible: or she buys the bread at the baker's, or at the confectioner's. These two possibilities do not have absolutely nothing in common, they share nothing. Geometrically we will say that they are orthogonal (perpendicular) and geometric representation in space (of the states therefore) will be:
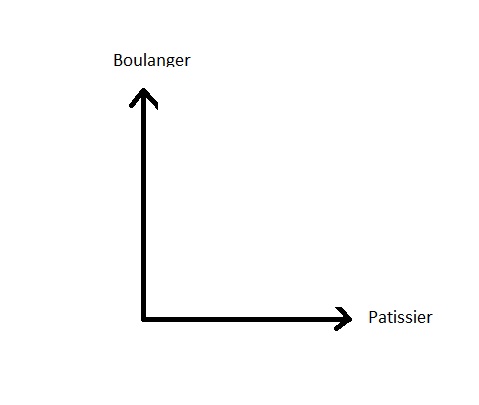
So we have two very distinct directions that have nothing in common.
If the arrow (vector) baker was leaning towards the arrow (vector) pastry shop
then that would mean that going to buy from
the baker is a bit linked with going to buy
in the pastry shop which is not the case, they are two
options incompatibles: orthogonal, i.e. at right angles: they do not share anything in terms of direction.
On the other hand, the state of the system, i.e. the state of mind
of the person is a so-called linear combination of the two states.
We say that we have a mixture of states. The real mixed state does not
does not correspond to anything observable: we don't know
not where the bread is bought.
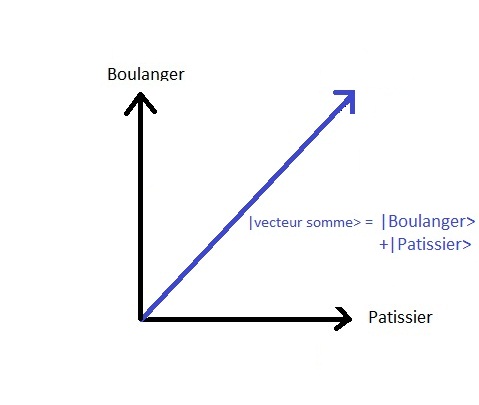
This linear combination of the two possibilities corresponds
to the sum of the two vectors representing the observable states.
The sum of two vectors is realized as follows : we do
From the end of the first vector and the vector
sum resulting from the beginning of the first one and ends towards the end
of the second.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
The state space was said to be a vector space, i.e. a space of directions, this implies that in the geometrical representation we can move the vectors without changing them nature, they remain the same vectors: they point in the same direction. Also to simplify the representation, all the vectors start from the same point to indicate that only directions exist in this space. This is called a vector space as opposed to to a space of points which is called in mathematics an affine space. ( The screen on which you are reading this text is an example of affine space where pixels represent points in this space.state sum vector img)
The geometric representation is obviously done in a space of points because a vector space
is a pure abstraction and can only be represented in the space we perceive with points (positions) different.
But this does not exist in the state space where all representations of a vector at different
positions in the representation space correspond to a single vector in the vector space.
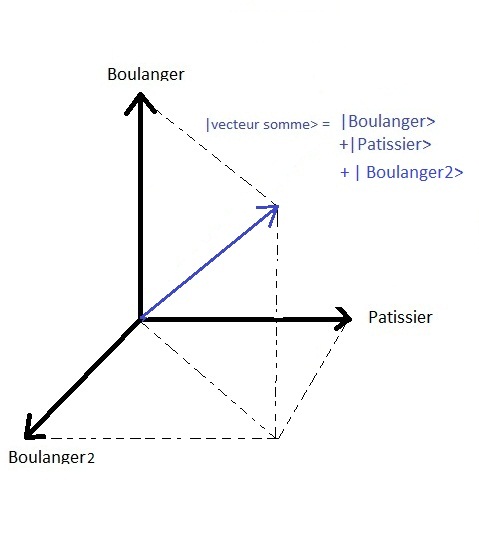
Thus we can represent the state in the following way :
Here the dimension of the state space is two. If there was a third option
with another baker in an adjacent street | baker2 > then the state space would be of dimension three, etc.
In physics, two-state systems can be modeled in the same way.
This is the case of the ionized hydrogen molecule. The hydrogen molecule
is composed of two hydrogen nuclei, i.e. two protons
and the fact that it is ionized means that an electron has been removed from it
out of the two that it naturally possesses. We take this example
because it is simple : "to a single electron".
The two possible position states for the electron are :
The geometric representation is:
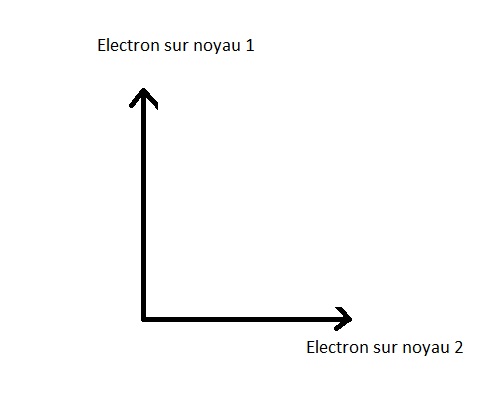
It is clear that the electron cannot be found (or rather to be found, that is to say : be observed) at the same time on core 1 and core 2, these states are orthogonal.
In the expression of the postulate, synonyms are used to designate the state vector, which is called indifferently
state vector, wave function or ket. These different names correspond to different mathematical aspects of the state vector.
We will see the wave function aspect in the explanation of the second postulate and the "ket" aspect in the third.
In summary, the quantum state is represented by the data of a vector (direction) in a vector space (of directions),
this vector is called "state vector".
In classical mechanics, the state is represented by the "material point" which is defined by its physical properties that are the position and the speed.
We can notice, and it is important, that in quantum mechanics the state of the system is totally independent
physical properties of the system. The state is defined in an abstract way and one could say "non physical".
This will be detailed in the presentation of the following postulates through the notion of "state vector representation base".
But we can notice that the first postulate makes the state vector depend only on time and not on position
which is the space. This means that the wave function is non-local.
Obviously relativity teaches us that time and space form a continuum and therefore if a formulation of
quantum mechanics takes into account at least special relativity, the state vector does not depend on
of time. This theory is the quantum electrodynamics or quantum theory of the electromagnetic field.
The special relativity being very linked to the electromagnetism by the fact that Einstein produced this theory
to remove the paradoxes that Maxwell's electromagnetic theory raised.
Quantum concepts were not conceived by pure imagination. Rather, they have been forged in the fire of experimentation
of microphysics that required these concepts to be properly represented.
Although totally abstract the quantum state is not less real for all that.
It is moreover this reality of the quantum state which often remains the most difficult thing to admit even if it is unavoidable.
The functioning of matter, which is the most concrete thing, is governed by something totally abstract.
Nevertheless it is impossible to circumvent this difficulty as this quantum concept is extraordinarily solid.
The cognitive situation is somewhat similar to the discovery of electromagnetic waves. These waves were first theoretically
discovered by combining Maxwell's equations that describe electric and magnetic fields.
Their combination provided a wave propagation equation with a constant velocity. It was an abstract notion
and new but the experiments tried showed that indeed the electric and magnetic fields produced waves
that could be controlled and used, which gave rise to radio communication.
We have seen that this speed was the measured speed of light.
In the same way the very abstract concept of wave function became very concrete in the experiments ofintrication_quantique and gave rise to the technological field of cryptographie_quantique
Postulat_II
"Any observable physical quantity 'a' is described by an operator 'A' acting in the state space; this operator is an observable.
" In classical mechanics we have seen that the properties of the material point, its speed and its position determine its state.
For example, the speed and position of a ball on a tennis court or of a planet in the solar system.
The position and velocity of a macroscopic object are determined at each instant and this completely defines the state of the system.
The evolution of the tennis ball in space defines at each moment the state of the game, if the ball is in movement, "out" or not or immobile on the ground after having taken the net.
And it is the history of its states that defines the match and its result.
On the other hand, in quantum mechanics the general state of a system reduced to a particle like the electron in the previous example is no longer associated with a particular position or velocity but with a mixture of all possible positions or velocities.
Moreover, we cannot observe all the properties of the system at the same time as in classical mechanics.
If the system is in a state of position, it is not in a state of energy and vice versa.
In the example of the bread we have states of position which are the baker and the pastry cook who indicate the place where the bread is bought but as we will see, they are not states of energy.
As in the example of the hydrogen molecule, the fact that the electron is located on the nucleus 1 or on the nucleus 2 represents positional states but they are not in themselves energy states of the molecule.
In a quantum system the different properties share the same state space but the states corresponding to different properties are not necessarily represented by the same directions in the space.
This means that if the space is two-dimensional then there will be two possible position states but also two possible energy states and that the energy states do not have the same directions as the position states.
In the case of the hydrogen molecule (ionized) the possible energy states are:
| State:énergie> = |related state> |unbound state>
in the "dynamic or energetic" representation of the hydrogen molecule.
The general state of the system is completely independent of the properties of this one so we can write for the bread:
| State> = |determination> |renunciation> = |baker> |baker>
For the hydrogen molecule calling El (related state) and Enl (unbound state) the energy states and P1 and P2 the position states, we have:
| State> = | The > | Enl > = | P1 > | P2 >
The fact that the state is independent of its observable properties and can be expressed indifferently from them is a fundamental characteristic of quantum mechanics.
The properties are represented by mathematical operators which, when applied to the quantum state, determine the possible states for this property.
An operator in mathematics is what makes a value evolve in the broad sense.
For example for addition the operator "3 " applied to "2" gives "3 2"="5" we changed the value from "2" to "5" by applying the operator "3 " (add value three) In quantum mechanics the operator makes the state evolve.
The postulate says that the operator "acts" on the state space.
Let P be the position operator and E the Energy operator (in reality the energy operator is noted H for hamiltonien_en which is the total energy function defined in a general way in mechanics by Hamilton by the sum of all energies acting on the system).
According to the second postulate these operators represent the corresponding properties (position and energy) of the system.
By applying (making it work) the position operator on the state of the hydrogen molecule we have:
P | status > = | P1 > or P | status > = | P2 >.
Applying the operator on the state means to observe the property corresponding to the operator, here the position.
In the same way with the energy operator.
H | status > = | The > or H | status > = | Enl >.
We can see that when we apply an operator to a state we make this state evolve towards a state belonging to this particular operator, we call this state "clean state" of the operator.
The result can be any possible state for the system and for the operator (the measured property).
The state "bonded molecule" is a proper state of the energy operator while the state "electron on the core 1" is an eigenstate of the operator position.
For the hydrogen molecule when in the bound state, the electron is in a state of indeterminate position between the two hydrogen nuclei.
We can say that the energy eigenstate is a linear combination of position states which can be represented as follows:
| The > = | P1 > | P2 >
We can say that the two states of position add up to a state of energy: when the electron is shared by the two nuclei, the molecule is bound, we say that the two positional states interfere constructively to form the energy state "bound".
in the same way the unbound state will be represented by | Enl > = | P1 >- | P2 >
we say that the two positional states interfere destructively to create the energy state "unbound".
If we take the bread analogy, the person's state of mind is a hesitation between going to buy bread from the baker or the pastry cook but also between going to buy bread or not buying bread.
We can say that the determination to go buy bread is a interférence_en of all the possibilities to go and buy bread, while renunciation is a interférence_en destructive of these same possible states.
We consider all the possibilities that can happen to the system and that are all included in the state space.
Geometrically, this can be represented as follows:
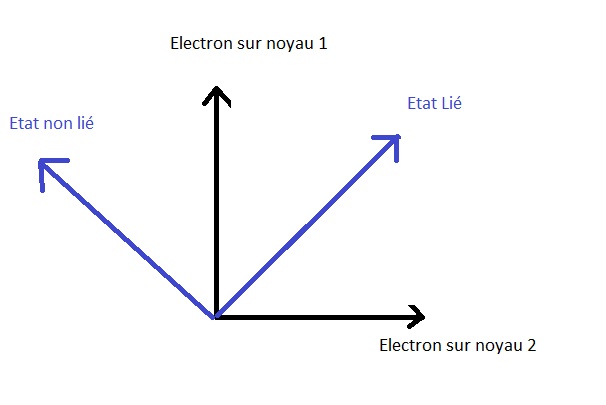
We notice that the observable energy states (bound or unbound states of the molecule) are also orthogonal because they correspond to possible energy options that are incompatible with each other.
The state of the system (state vector) is itself independent of its representation in the state space either with respect to energy or with respect to position.
We say that the eigenstates related to an operator are a representation basis of the state vector (here blue or black base) Thus we have for the state vector a representation basis for the position operator and a different representation basis for the energy operator.
1.1.2.Principle d incertitude de Heisenberg
The principe_d_incertitude_de_Heisenberg follows directly from the postulates of quantum mechanics.
We have seen that in general the eigenstates of two observables are not represented by the same vectors and that an energy state for example will be represented by a linear combination (superposition) of positional states.
In this case, it is clear that it is impossible to observe both the position property and the energy property of a system during the same measurement since their eigenstates are incompatible.
Mathematically we say that the operators do not switch.
That is to say that if we apply successively the two operators to the system in a different order then the final state will be different.
In practice, in a quantum experiment, a large number of particles are observed which gives a global statistical result in which it appears that the more precision we have on the energy value, the less precision we have on the position and vice-versa.
1.1.3.Representation of the wave function in physical space
The difference between the state vector and the wave function is the fact that the state vector is independent of the physical space while the wave function is not because it propagates in it.
In quantum mechanics we say that the wave function is a projection of the state vector in physical space.
In the image below we have represented the wave aspect (wave function) of quantum states
to visualize how the wave interferes destructively or constructively by addition or subtraction.
The fundamental functioning of a wave is the same whether it is a quantum wave, a wave
electromagnetic or for example a wave on the surface of a body of water (vaguelettes).
A wave always has a trough and peak oscillation (of the wave) around a mean value (the flat surface of the water).
The pluses add up to one another (as well as the less) and the pluses and minuses subtract and cancel each other out.
For example, if a wave trough meets the top of another wave, the two cancel each other out to leave
the surface of the water is flat at the point of overlap.
1.1.3.1.Hydrogen molecule states
The wave states of an atom or a molecule correspond to ondes_stationnaires_en
which are waves that do not propagate but remain mainly localized in a limited area
of space, here around the hydrogen nuclei.
The second postulate introduces the operators that are applied on the states to transform them.
We can therefore say that the state vector represents the static aspect of the quantum reality, while the operator represents the dynamic aspect of this same reality.
The third, fourth and fifth postulates describe the very process of observing a quantum system.
Postulat_III
Measure : possible values of an observable "The measurement of a physical quantity A can give only one eigenvalue of the corresponding observable A among all possible ones.
" We have seen that the observable states of a property of a quantum system are called "eigenstates" (of this observable).
To each "eigenstate" is associated an "eigenvalue" which is the result of the measurement.
For example for the hydrogen molecule it will be the energy level of the molecule that is different if the molecule is in its bound or unbound state.
In the bread analogy, we can imagine that the result is the change in the amount of money in the wallet that has decreased when the bread was purchased.
The eigenvalue is a number while the eigenstate is, as we have seen, a vector.
Up to now we have only used the direction of the vector which is also associated to a dimension of the state space because it is the most important notion concerning the quantum state.
In mathematics the natural value associated with a vector is its length.
This length is abstract (it is not physical space so it is not measured in meters).
For this reason we created a more general term referring to the length or the scale from where the no of "scalar value".
The scalar is therefore the numerical value associated with the length of a vector.
If we multiply the length of a vector by a number we will obtain a vector whose length will be a multiple of the initial value, it will be at another scale of magnitude, its new value "scalar".
Here we are observing the energy of the system using the energy operator.
We have seen that in this case the application of the energy operator on the state gives the two possible energy states simultaneously:
H applied on the | status > will give either the state | The > (to link) associated with the energy El is the state | Enl > (for unrelated) associated with the energy Enl (the energies are the eigenvalues of the energy operator).
The logical operator "or" (or non-exclusive) is represented in quantum mechanics in the state space by the addition of the vectors noted " ".
So we have:
H | status > = The | The > Enl | Enl >
The global state is a superposition of the possible eigenstates where El and Enl represent, as we have seen, respectively the energy values of the two states.
To represent the fact that only one value is possible during a measurement, we use a property of vectors called projection.
Below is the image of the global state projection |Psy> on the energy state "bonded molecule" | The >
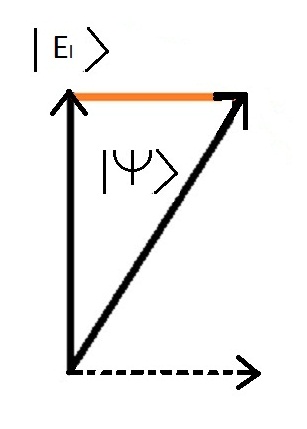When the physical property is measured on the system, the postulate is that the measurement gives a unique value and that this value corresponds to a particular state of the system called "eigenstate", the value obtained being named "eigenvalue".
In the previous equation we add possibilities and not values, so we do not have E = El Enl, adding a vector does not work like adding a value (scalar).
We will see later that the addition of possibilities will lead not to the sum of the energies but to the average value of the energy which is the sum of the values (ici El Enl) divided by the number of values added (ici 2).
The average value of the energy would be E = (El Enl)/2.
In reality it is a little more subtle than that because the average value of the energy also depends on the probability of existence of each state of energy, it is thus an average value weighted by the probability of each state.
This is precisely the subject of the fourth postulate.
Postulat_IV
Born postulate : probabilistic interpretation of the wave function "When we measure the physical quantity A on a system in the normalized state "phi", the probability P (An) to obtain the eigenvalue An of the corresponding observable A is |Cn|².
Where Cn is the amplitude of the wave function projected onto the eigenstate |phi n> corresponding to the observed eigenvalue An.
So far we have only talked about states, observable eigenstates and their associated eigenvalues.
By convention the length of any state vector is 1, the reason is that the state vector conveys the existence of the system (first assumption) and that in terms of probability, the affirmation of the existence of the system corresponds to a certainty.
In probability the certainty is 1.
When you have a 1 in 1 chance of anything (1 divided by 1 equals 1) we are in the certainty.
A probability of less than 1 is less certain than full certainty.
For example, the chance of winning the lottery by playing only one grid is 1 divided by a few million.
This means that in the end only one or almost one will win the millions at the draw ! The draw in quantum terms is "the observation of the winner".
The amplitude of the wave function is the same as the length of the state vector.
We have seen that a scalar is a simple numerical value.
This designation appears also by comparison with more complex numerical values composed of several numbers like the vector which when one wants to represent it numerically requires the use of several numbers.
(if we follow this line of development we arrive at the concept of "tensor" very used in physics, tensor of elasticity, of curvature of space-time...Postulate IV nweb).
_
When we project a vector on another one, the length carried from the first one on the second one is a number.
We have thus realized an operation that associates a number to two vectors, which we call scalar to indicate that the particular result of this operation of two vectors does not give a third vector as in the addition of vectors but a number (scalar).
We call this operation the scalar product: The scalar product is an operation that from two vectors gives a number.
This number is the orthogonally projected length of one vector on the other.
The English word "bracket" which means hook and refers to the characters "<" et ">" These brackets are traditionally used in mathematics to represent the average value of a quantity. The image below represents the projection of the general state | Dogs > on the two energy states | Dogs l > and | Dogs nl > (which are the same as the states | The > and | Enl > it's just a difference in notation)
When we considered the states "buy bread" |baker> and |baker> we implicitly considered that we could observe one and the other in an indifferent way, i.e. having an equal probability to occur.
"The sum of the square of the lengths of the two sides is equal to the square of the length of the hypotenuse" In our case the hypotenuse corresponds to the state vector |phi> and both sides to the projections of |phi> on the two eigenstates |baker> and | Epicier>. If we consider the expression | Dogs L >< Dogs L | composed of a ket and a bra and applied to the ket | Dogs > we obtain | Dogs L >< Dogs L | Dogs > where < Dogs L | Dogs > is the probability amplitude of obtaining the state | Dogs L > so we have : | Dogs L >< Dogs L | Dogs > = | Dogs L > To = To | Dogs L > we see that the final state is the state | Dogs L > associated with the probability To The expression | Dogs L >< Dogs L | is therefore an operator that has made the initial state evolve | Dogs > to the final state | Dogs L > and this with a probability Al.
1.2.2.Operator partition of the unit
Consider the following operator:
| Dogs L >< Dogs L | | Dogs nl >< Dogs nl | which is the sum of the evolution operators towards the eigenstates of an observable (here the energy : bound and unbound state).
It is interesting to note how the vector representation of the state and its decomposition according to an orthogonal basis allows to naturally represent the amplitudes of probabilities and thus the probabilities of the evolution of the system during a measurement.
Postulat_V
Measure : reduction of the wave packet If the measurement of the physical quantity A, at time t, on a system represented by the vector |phi> results in the eigenvalue An then the state of the system immediately after the measurement is projected onto the eigensubspace associated with An This postulate is also called "wave packet reduction postulate".
It is probably the greatest conceptual revolution of quantum mechanics to introduce the fact that the observation of the system makes it evolve, whereas in non-quantum physical theories it is only the dynamical equation that is responsible for the evolution of the system.
Traditionally the dynamic equation of a mechanical theory expresses how energy acts on the system to transform it.
L_expérience_du_chat_de_Shroedinger is a thought experiment imagined by the physicist Erwin_Shroedinger to reflect on the problem of measurement in quantum mechanics directly related to the fifth postulate.
We can notice the link between the observer and the wave function: neither of them is material ! We could say that what is material is what lies between the two: observation.
The wave function and the consciousness represent the two faces of the same reality transcending materiality and
at the very origin of this materiality.
obviously physicists as a whole do not generally go that far in the vision of quantum reality.
The standard position in this area is theinterprétation_de_l_école_de_Copenhague.
This position emerges from the situation of the human observer who experiences a classical world and considers it as the absolute reference.
We can define different degrees of distance from this position:
It should be noted that this point of view is no longer scientifically tenable since the Aspect experiment which validates the mechanics
quantum in its most disturbing assertions.
At the same time this quantum mechanics is the most verified theory in the history of science.
This point of view is thus reduced to a simple "materialist belief".
This view was nevertheless Einstein's, but unfortunately he did not live long enough to
see the resolution by the Aspect experiment of the paradox he defined with the physicists Podolsky and Rosen in his famous article:
the Paradoxe_EPR.
Here the classical world in which we live does not represent the totality of the world any more because it exists
an absolutely strange quantum world to which we do not have access but with which we can deal by
through the quantum theory.
The stable physical world we know is made up of only three quantum particles: electron, proton and neutrino.
This third point of view removes all the quantum paradoxes by saying finally and simply that one should not
not looking for an interpretation (classic) of the quantum theory but that it is simply necessary to accept it
as it is (Copenhague) and finally recognize the supremacy of its position.
We can thus predict that the quantum model will never be put in default. Since its creation we see more and more how quantum reality
intervenes in the understanding of the world around us and more particularly in the field of the living, macroscopic system of a great coherence... quantum.
Here are two fairly recent examples:
Postulat_VI temporal evolution of the quantum state. _ H |Phi(t)> = i h/2*pi d |Phi(t)> / dt _
0,000000000000000000000000000000000662607004 When we combine this constant with other fundamental constants such as the speed of light or the universal gravitational constant, we deduce the minimum quantities of the different units of physics : Planck length, Planck time, etc....
1.5.Condensed poetic expression of the postulates
The following is an attempt to group all the postulates in a single aphorism:
"What is possible is accomplished, under the eye of the conscience, only what is possible is accomplished.
Quantum mechanics is the greatest revolution of our modern scientific era because it definitively destroys the materialist position, thus opening the way to a development of humanity where science and consciousness will be united again.
The decisive experiment that allowed to settle the Einstein-Podolski-Rosen parodox
made in 1982 by Alain Aspect, researcher and experimenter at the quantum optics center of Orsay
was based on photons.
A detailed description of the underlying theory can be found in the book
by Bernard d'Espagnat "A la recherche du réel".
That same year, I was at the university and Alain Aspect came to present
its results in Toulouse, in the Maxwell amphitheater of the Paul Sabatier University.
After presenting unequivocal measurement results, he left
the assembly without a voice (or not, the amphitheatre was filled with professors and researchers).
At the end of the presentation, after a moment of significant silence, when the floor was opened, the
was given to the assembly, only one researcher stood up (my relativity teacher) and asked this question:
And you find it easy to live with that now?.
Aspect, on the defensive, replied that he had not said that, that he had done
an experiment and that the result was that, but that he was careful not to
give any interpretation.
I learned years later from someone who had been in contact with him that he was
pro-einsteinian and that he had expected that quantum mechanics would be put in default.
I was on the side bay in the third row, all alone and I was amused because I didn't understand
why they had a problem with it, or rather I understood it only too well.
When the experiment was in its early stages but the outcome was only a matter of time,
the polemic became very strong, even sulphurous.
When the scientific community of physicists was in shock, we
could wonder what was going to happen.
It took time for the information to be digested, we can see in 2020 that the situation
has evolved quite a bit, just look at this lecture given at the Polytechnic
by Hervé Zwirn, Director of Research at the CNRS
_x_sciences_de_l_homme_et_de_la_société_x_shs_mécanique_quantique_le_monde_existe_t_il
This experience had (or should have for the majority) the same kind of effect in the community of
physicists that the discovery of radio waves (electromagnetic waves) who have
to the abstract concept of the electromagnetic field a much more vivid reality.
The discovery of non-separability and its observation at the
physical level gives life to the concept of independent reality, i.e.
A first conclusion that we can bring to the first postulate of mechanics
quantum is that:
The reality of a quantum system (and in fine, all systems are quantum! x sciences of man and society x shs quantum mechanics does the world exist nwebs) is underpinned by
by an abstract space of possibilities unobservable in itself (non-physical and
independent of all space-time contingencies) but nevertheless real, since it is
from this level of abstract functioning that the concrete reality emerges (observed).
To sum it up in one word: it is about omnipresence and omniscience since it contains
all information about the physical system in a non-local way.
Moreover, to be complete, this is related to the observer who obviously cannot be physical.
The evidence appears then that the observer and the independent reality maintain a close relationship:
they are both non-physical and interact in terms of information, knowledge, perception.
The Matrix movie can be considered as an allegory of quantum reality.
We can give and we have given to this universal consciousness all the names we want
but these will never exhaust the infinite power of this consciousness.
The average value of the energy will be noted for example < E >.
We have seen that the quantum state is also called "ket" noted | ket > the other part of the bracket is the "bra" which is a particular operator noted < bra | It is the physicist Paul_Dirac which is at the origin of this separation in two of this word to make appear a dynamic of operator and vector in the operation of taking the average value.
If we apply the "bra" on the "ket" we get < bra | ket > which is the number resulting from the application of the operator
We have here a dual relationship between the bra and the ket.
For a state (ou ket) "| Dogs >" le bra sera "< Dogs |" the duality between the two is represented as the image in a mirror The ket is a vector while the bra is an operator, applying the bra on the ket gives a number.
In a general way in an expression what is on the right of the ket is an operator, the result of an operator on a state (vector) is either another state (vector) either a number that represents a measurement result or a probability.
For every ket there is a corresponding bra and the operation which allows to pass from the ket to the bra is called the hermitic conjugation and is noted by a star.
Thus ( | Dogs > ) * = < Dogs | or (
This can be analogously compared to a Vedic aphorism in which the creator of the universe speaks: "turning on myself, I create again and again".
We can also see the same form in the first creation story of Genesis: let there be light and light was and D.
God saw that the light was good.
< let the light be | and the light was > = and D.
God saw that the light was good.
< or | light². | barrel > = D.
God saw that the light was good.
The fact that D.
God saw that the light was good is clearly the result of an observation.
We could call all this the quantum alphabet and syntax.
The alphabet consists of only one letter | Dogs > and that's "the being" (or the state that is the affirmation of being) The dual operation * shows its dynamic operator value ( | Dogs > )* = < Dogs | All their combinations make appear the quantum grammar.
An example is the application of the operator < Dogs | on the state | Dogs > gives < Psy|Dogs > which is also the projection of the state |Psy> on itself and is therefore 1.
This can be translated trivially by the sentence: "Psy participates 100%. (100/100=1) to Psy".
< Dogs L | Dogs > is the projection of the general state of the system on the bound energy state of the example of the H2 molecule and represents the amplitude of probability to obtain the bound state during an observation.
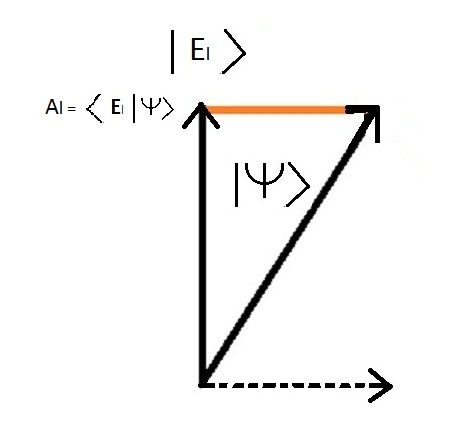
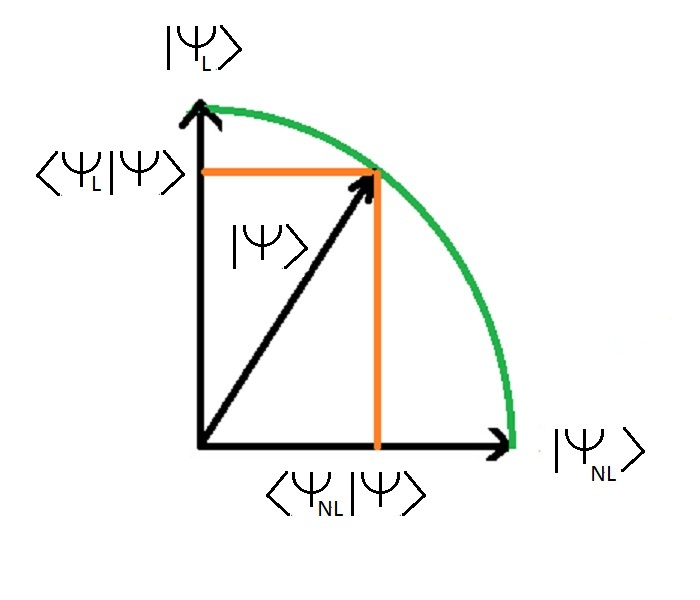To = < Dogs L | Dogs > By taking the square of the amplitude we obtain the probability The probability of the state | Dogs L > is: Pl = Al² = ( < Dogs L | Dogs > )² 
The two values < Dogs l | Dogs > and < Dogs nl | Dogs > represent the length of the state | Dogs > (which is 1) projected on own statements | Dogs l > and | Dogs nl > < Dogs l | Dogs > is the projection of the state | Dogs > on the clean state | Dogs l > < Dogs nl | Dogs > is the projection of the state | Dogs > on the clean state | Dogs nl >
We speak then of equiprobable state.
But the characteristics of the system may be such that this is not the case, for example if the baker is closer to home than the pastry chef and it is very cold the probability of the state |baker> will be stronger than that of the state |baker>.
This is represented in the image below where Ab is greater than Ap.
(A is the probability amplitude).
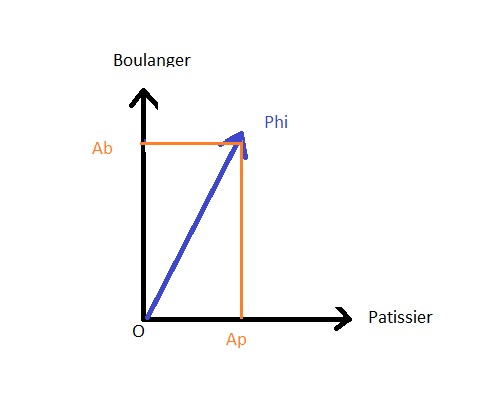The projection of the state |Phi> general on the state |baker> has the value Ab which corresponds to the amplitude of probability to obtain this state from the general state |Phi> in the same way for Ap which is the amplitude of probability of obtaining the state |baker>.
The quantum eigenstates are always orthogonal, i.e. they are at right angles to each other and therefore follow the theorem of . Pythagore
for the right-angled triangle.
The postulate says that the square of the amplitude of the wave is the probability.
Considering the general state of the system is simply considering that there are: the probability of the effective state of the system is always equal to 1.
This is what the postulate mentions by saying that the state |phi> is normed and its norm is always equal to 1 by convention since it is a probability.
Mathematically we note < phi | phi > = 1 = | |phi> | ² (the last expression represents the square of the norm of the vector, the norm of the vector being its length) Then this probability is divided into several lower probabilities corresponding to each eigenstate but with the constraint that the sum of the squares of the amplitudes of the eigenstates of the system is always equal to 1 which is the certain probability.
In our case we have:
Ab² Ap² = 1 The sum of the probabilities of all possible states of the system must be equal to 1.
We can say that the existence of the system is distributed on all its possibilities of existence but without there being loss of existence so that its existence is preserved.
Indeed, if the total probability decreased, this would mean that the system would have less chance to exist and by reducing the probability of its existence to zero, it would disappear ! The amplitude of the state or wave function can be positive or negative just as we can have the peak or trough of a wave.
The probability amplitude is therefore either negative or positive, which is what we have represented in the image on the bound and unbound states of the hydrogen molecule by the symbols plus and minus - .
(. états molécule hydrogène Pythagore) But the probability which is the square of the amplitude (or square of the standard ) is therefore always positive, which is normal for a probability.
Indeed, we can imagine a certain probability, then less certain until little certain or even null but a negative probability does not make sense.
On the other hand, the probability amplitude can be negative.
Let's suppose that we have two equal probability amplitudes but of opposite signs propagating towards each other (they are waves).
If we consider the probabilities when these amplitudes are at the same place, then the amplitudes of opposite signs cancel and their square is also zero.
The probability of observing something will be zero.
But if the amplitudes are separated their square will be positive (more by more is positive but less by less is also positive) and therefore the probability of observing something will no longer be zero.
When we talk about quantum mechanics, we think of its probabilistic character as a game of chance, but what we generally ignore is that these probabilities are underpinned by something much more disturbing, which is the amplitude of the probability wave and which gives quantum mechanics its reality.
It is an evolution operator that made the system evolve towards the state of bound energy during an observation.
This leads us naturally to the fifth postulate which describes how the system evolves during a measurement.
If we apply this operator to the ket | Dogs > on a :
( | Dogs L >< Dogs L | | Dogs nl >< Dogs nl | ) | Dogs > or | Dogs L >< Dogs L | Dogs > | Dogs nl >< Dogs nl | Dogs > which gives | Dogs L > To | Dogs nl > Anl or even To | Dogs L > Anl | Dogs nl > which is the decomposition of the state | Dogs > in sum of its own energy states | Dogs > = To | Dogs L > Anl | Dogs nl > The operator has not changed the state | Dogs > but simply decomposed it into its different parts, for this reason it is called the "partition operator of the unit".
First of all let us elucidate this notion of "sub-eigenspace".
It is just a generalization of the decomposition of the state into its eigenstates.
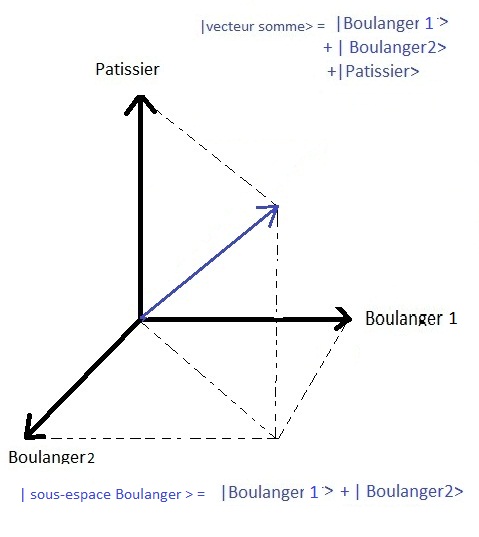
Let's take the example of bread with two bakers and a pastry chef.
If the distinction of the type of business is not observable (is not an observable of the system)In the case of a measurement, there will be no need to distinguish whether it is baker 1 or baker 2, we will be satisfied with knowing that the state has been projected to the baker's own subspace which corresponds in fact, in the diagram below, to the horizontal plane populated by the bakers ! If there were an observable that allowed us to observe which baker the bread was bought from, during this measurement the state would be projected to one or the other of the bakers, lifting the indeterminacy during the measurement.
But if we do not observe this property of the system then the system remains in this state of superposition of the baker wave functions.
We say that the state is degenerated.
In practice, when several eigenstates have the same eigenvalue (same energy) have said that these states are degenerate.
By applying to the system an additional energy constraint which will modify the energy of the degenerated states so that there is no more equality, we will lift the degeneracy.
Quantum physics is essentially concerned with understanding the structure of the microscopic world which is essentially made up of resonances (standing waves) which are eigenstates of the total energy operator of the system (Hamiltonia).
The fifth postulate says that during the measurement, the state of the system evolves towards the state whose eigenvalue has been measured.
It is this so-called postulate of "reduction of the wave packet" or "collapse of the wave function" that gives the geometrical representation of the projection of a vector its physical reality, since the system physically evolves in this operation.
In this fifth postulate we have seen that the measurement itself transforms the system.
In the case of quantum mechanics such a dynamic equation also exists and it is called the Shroedinger equation .
So in mechanics we have two mechanisms for evolution: the action of energy in time and the action of observation out of time.
It is this equation that constitutes the sixth and last postulate of quantum mechanics (see below).
The fifth postulate implies the observer of the system in the evolution of the system.
Thus in quantum mechanics the observer is no longer independent of the physical system.
The observer and the physical system form an inseparable whole.
One could say that the observer is embedded in the system (but not in the sense of quantum entanglement which only concerns the wave function).
The phenomenon of quantum entanglement was mentioned above, which comes from the fact that a quantum system made up of several particles is described by a single wave function (first assumption) even if the particles are likely to have moved away in physical space.
According to the fifth postulate, during a measurement the wave function collapses to a proper subspace instantaneously affecting at the same time the state of all particles composing the system.
It is this implication of quantum mechanics that Einstein officially could never admit because, in his opinion, it violated the propagation limit of any physical interaction defined by the speed of light.
According to Einstein's theory of relativity no energy can move faster than the speed of light.
Light obviously moves at the speed of light and it can only do this because it is pure energy, that is to say without mass.
Massive particles must therefore necessarily move at a speed lower than the speed of light.
The "physical" resolution of this quantum paradox was carried out by an experiment known asexpérience_d_Aspect.
This experimentation proved indisputably that the wave function did not depend on the physical space in which we live: its evolution during the collapse due to the observation is carried out in any point of space at the same time.
Aspect's experiment has been reproduced many times under more and more sophisticated conditions to push quantum mechanics to its limits, but it has never given in ! We say that the quantum theory is a non-local theory.
The terms used "non-locality" or "non-separability" are equivalent.
We can therefore say that the quantum wave function transcends physical space, it even transcends space-time since since Einstein's theory of relativity we must consider space and time as aspects of the same deeper reality : the space-time continuum.
A more recent experiment carried out in a relativistic framework and conducted in the continuity of Aspect's experiment has confirmed the validity of quantum entanglement in the relativistic framework.
( cf Expérience_d_Antoine_Suarez found on the physicist's site Philippe_Guillemant which offers a vision integrating the quantum reality ) This last experiment is important because in a physics experiment one can only measure values within a certain range.
Thus in the first Aspect experiment the detectors of correlated photons (in a single quantum state) were only a few meters apart.
This was enough to demonstrate that quantum entanglement could not be due to an unknown physical phenomenon (hidden variable) taking place at an infra luminous speed.
The speed of such a phenomenon would necessarily be superluminal.
Although such a supraluminal speed is hardly acceptable because of Einstein's theory of relativity, Aspect's first experiment did not allow to completely revoke this possibility.
With Antoine Suarez's experiment this is done because it is even the possibility of a causality between the detections of the two correlated photons that is suppressed, because the relativistic reference frames in which the detections are made, do not allow a "^before" and "after", essential condition for a causality: neither of the two photons is detected before or after the other because these detections are not made in the same time reference frame.
In a relativistic quantum theory the wave function can no longer depend on time as we have seen in the first postulate.
The reason is that time is brought to the same level as position, i.e. an observable property of the system, and that the wave function is independent of the properties of the system (second premise).
In such a theory the wave function would be | Dogs > and no longer | Psy(t) > .
Time would be an observable T in the same way as the position P.
The particularity of this completely unrealistic thought experiment as presented with a "real cat" is to make one think about what the observer is in quantum mechanics.
You have seen in the postulates dedicated to the measure (or observation) that we do not go into detail about what the observer is.
The postulates say that there is an observer who makes the measurement but do not say anything more about the nature of the observer ! In this experiment, a cat is isolated in a box so that it cannot be observed (quantified) in any way.
This supposes that the cat can be considered as a quantum object, which is not the case in practice although in theory the cat can be considered a priori as a physical system, being composed of atoms which are and are well described by quantum mechanics.
In this box there is also a vial containing a gas that is deadly for the cat and a particle detector that opens the vial if a particle is detected.
If a particle is detected the cat will be dead, if it is not detected the cat will be alive.
As long as we have not observed the state of health of the cat "quantic" this one remains in a general quantum state called superposition of the observable eigenstates, which are | live cat > and | chat mort > so we have | chat > = | live cat > | chat mort > Our quantum system is made of several components: the cat, the detector, the particle.
All these subsystems must also be considered in the establishment of the wave function, so we have: | particle > = | particle present > | absent particle > and | sensor > = | detected particle status > | undetected particle state > The mathematics associated with quantum mechanics shows that the global system that we will call "shroedinger" is : | shroedinger > = | cat, detector, particle > = | chat> ¤ | sensor > ¤ | particle > where ¤ represents the "tensor product" of the state vectors.
Being found within the same quantum state, we say that these different subsystems are intricate.
This product behaves like a usual product operation, it is distributive : A * ( B C ) = A*B A*C In quantum terms we can develop the general quantum state.
Let's start with the system composed only of the detector and the particle.
| detector, particle > = | sensor > ¤ | particle > = ( | detected particle status > | undetected particle state > ) ¤ ( | particle present > | absent particle > ) by developing :
| detector, particle > = | detected particle status > ¤ | particle present >
| undetected particle state > ¤ | absent particle >
| undetected particle state > ¤ | particle present >
| detected particle status > ¤ | absent particle >
Erwin Shroedinger nweb The first two states are easily understood, if the particle is present it is logical that it is detected and not if it is absent.
The following two states are very unlikely but nevertheless exist according to quantum mechanics for which everything is only a probability amplitude.
For the state | shroedinger > complete it would be necessary to develop further with the states of the cat, which would lead us to a wave function with eight possible eigenstates, two of which are highly probable and six highly improbable.
The two probable states are:
| chat mort > ¤ | detected particle status > ¤ | particle present > | live cat > ¤ | undetected particle state > ¤ | absent particle > As long as we have not observed the system, which corresponds for example to opening the box, we are in a state of superposition where the cat is in an indeterminate vital state.
This is where the paradox lies.
But we can push the reasoning further and this is what the physicist did Eugène_Wigner Nobel Prize in Physics.
This is the théorie_de_l_influence_de_la_conscience He considered that the eye of the observer who sees the cat dead or alive is also a quantum system with two states: | oeil > = | eye sees the dead cat > | eye sees the cat alive > The states of the complete wave function would then take into account "hallucinatory" states where the eye would see dead, the cat alive...
But one could thus continue to consider the chain of the measurement until the brain of the observer which is also composed of atoms.
So the question is : at what moment the measurement is actually carried out, i.e. the collapse of the wave function and therefore the choice of the result of the experiment: dead or alive cat.
Wigner says that nothing material can cause the collapse because all the materiality is susceptible to be described by the quantum mechanics and thus is part of the wave function and one can also very well consider the wave function of the universe.
If nothing material operates the measure, there remains only something immaterial which does it and that Wigner identifies it with the consciousness which identifies finally what is the observer.
In his interpretation The observer is the consciousness .
This brings us closer to the conception of "independent reality" or "veiled reality" introduced by the physicist Bernard_d_Espagnat for the philosophical understanding of quantum mechanics.
bernard_d_espagnat_physique_quantique_et_réalité_la_réalité_c_est_quoi ;Retrieved from \" https://www.
youtube.
com/watch?v=Jd8FiWJ5v8M; This also brings us closer to the Vedic conception, in ancient India, of material reality described as "Maya" or the illusion of the senses.
This Maya being made by the infinite interrelations between three elements : richi, chandas and devatta which are the subject, the object and their relation, the knowledge (spiritual: of the mind) or the perception (material: of the material).
The observer consciousness and the non-material quantum reality creates the phenomenological material reality.
In this respect, the film Matrix is an allegory of reality, the only difference, and it is an important one, is that it is not machines that create the illusory reality but consciousness itself.
Thus we can define consciousness as being the putting in relation of the subject with the object by the perception or knowledge.
The following triads are equivalent:
samhita_tab_en
veda philosophy quantum physics
rishi subject observer connoisseur observer
devatta perception (subject/object relationship) observation knowledge observable chandas object observed known result of the measurement: eigenvalue of the observable
This position says that between two measurements there is no object and that the only object that exists is "the observed object".
The classical term corresponds to what humanity as a whole perceives in the same way. But this position is in conflict with
the quantum reality which is thus perceived as totally paradoxical.
The central or pivotal problem between quantum reality and classical reality is that of decoherence.
The decoherence is the passage from a quantum operation to a classical operation.
That is to say that when the system has decohered, it is classically describable because the quantum aspect has vanished.
When we study quantum mechanics, we are shown that it reduces to the laws of classical mechanics when considered at macroscopic scales.
Decoherence is the fact of passing from the description of the physical system by a single wave function to that of a separate set of corpuscles.
When the wave function of a set of particles "decoheres" in the collapse of the measurement the wave aspect of quantum mechanics disappears and only the corpuscular aspect remains.
The physical theory that deals with the description of an important set of corpuscles is the statistical thermodynamics that takes its foundations in the quantum theory through the quantum statistics of Böse-Einstein and Fermi-Dirac.
This theory, constituted in the 20th century, makes it possible to recover from microscopic considerations the results of the macroscopic thermodynamics of the 19th century.
Thermodynamics operates in the classical world of decoherence while quantum mechanics operates in the quantum world of wave coherence.
Decoherence is the passage from the quantum world to the classical world.
Mastering decoherence is the challenge to produce the quantum computer.
Alain Aspect in his conference Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_révolution_quantique admits in this regard (at 1H23mn) that if the quantum computer can one day become a reality, he does not see why the brain could not be one.
Thus the two non-physical realities: the consciousness and the wave function could be in reality only one.
The state . Phi
of any non-relativistic quantum system is a solution of the time dependent Schrödinger equation: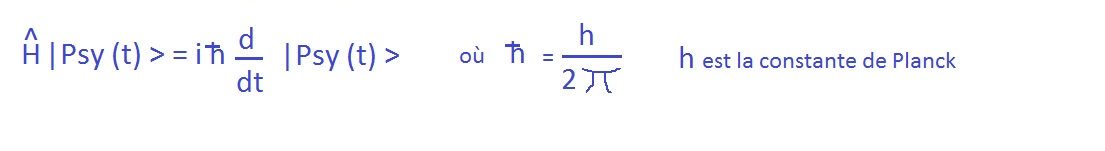 
The sixth postulate is the. équation de Schrödinger
.
This is the dynamic equation of quantum mechanics.
It simply means that it is the \"total energy\" operator of the system or Hamiltonian noted "H", which is responsible for the evolution of the system in time.
(Traditionally in quantum mechanics, operators are given a hat to distinguish them from other mathematical objects such as eigenvalues.équation de Schrödinger) The form of the equation shows that by applying the Hamiltonian operator to the wave function of the system, we obtain its derivative with respect to time, i.e. how it varies in time.
(for a delta t variation of time so "dt" we have a variation "d | Psy(t) >" of the wave function).
So if we apply the Hamiltonian operator (énergie) to the wave function we obtain its evolution in time.
It is clear that it is the energy that makes things evolve.
Energy and time are intrinsically linked.
We say that they form a couple of conjugate variables.
This equation is only valid in the non-relativistic frame.
In the relativistic framework the valid equation is the Klein-Gordon equation.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf The Hamiltonian operator H is composed of all the energies which intervene on the system.
These energies are of two kinds: kinetic energy and potential energy.
Kinetic energy is the energy contained in a moving mass.
A pebble thrown into a window breaks it by virtue of the kinetic energy it has acquired when given a certain speed.
If there are several successive windows, the greater the speed of the stone will be and the more windows it will pass through.
The potential energy is due to the force fields that apply to the system.
If we drop a pebble on a window on the ground, it will acquire speed because of the gravitational potential energy that it possesses due to the fact that it is far from the earth..
The more time passes, the more the potential energy is transformed into kinetic energy and when the pebble arrives at the ground, it breaks the window by virtue of the kinetic energy it has acquired at the expense of its potential energy which it has lost.
If we push it into a well, it will continue the same process until its potential energy is totally exhausted, if possible..
If we consider the movement of a pendulum (a pebble attached to a support by a string) this one oscillates, that is to say that from the starting position (at a certain angle from the vertical) where the pebble is dropped, it will accelerate until the string is vertical, then it will slow down until it stops on the other side in a position symmetrical to the starting position and vertical.
The pendulum transforms its potential energy into kinetic energy and then its kinetic energy into potential energy and this cyclically.
If the system is not subjected to any other force, the movement does not stop.
In practice, there are always frictional forces that dissipate energy into heat until it is exhausted.
But this last point is only true in classical mechanics because in quantum mechanics there is no friction ! Another system where there is a cyclic transformation between potential energy and kinetic energy is the motion of a satellite around a planet, for example the moon and the earth.
The solution of classical mechanics in this case shows that the trajectory of the satellite is an ellipse, that is to say that there is a moment when the moon is farthest from the earth (maximum potential energy and minimum kinetic energy, apogee) and another time when the moon is closest to the earth (minimum potential energy and maximum kinetic energy, perigee).
The systems we have just described are classical systems but they have their correspondence in the quantum domain.
For example the model of the pendulum in quantum mechanics is called the harmonic oscillator and the model of the satellite corresponds to the model of the hydrogen atom: an electron satellite of a proton.
In quantum mechanics kinetic energy is an operator involving mass, and potential energy is of course also represented by an operator whose form will depend on the energies involved: electrical, magnetic potential, ...
The way in which the mass intervenes in the Shroedinger equation, comes from the previous work of Louis de Broglie who established the wave-corpuscle duality: to each particle of matter we can associate a wave whose frequency is proportional to the mass.
This from the two energy formulas: E = m c² which is the formula of the energy of the special relativity of Einstein : the mass is equivalent to the energy E = h * nu which is the Planck-Einstein relation explaining the photo-electric effect : the energy is proportional to the frequency.
Thus we see that in the Shroedinger equation is integrated a result of Einstein's special relativity.
It is important to understand that the energies involved exert a constraint on the system, i.e. on the wave function.
When dealing with oscillatory systems like the harmonic oscillator (pendule) or the hydrogen atom (the satellites)the constraint of the energies has the effect of localizing the wave function in a region of space.
For example, a classical system subjected to no force (a meteor lost in the inter-sidereal space where we can neglect the gravitational forces of the stars) will move in a straight line indefinitely.
The quantum equivalent is a plane wave that propagates indefinitely, as for example a photon that is not subject to any force (photons are particles without mass or electrical charge of any kind and are therefore not subject to any force or energy).
When the wave function has a cyclic solution (localized wave function) time no longer has the effect of moving the parts of the system away from each other indefinitely.
The electron will remain localized near its nucleus which is the proton in the case of the hydrogen atom.
At the same time, if the quantum wave propagates cyclically in a finite region, it overlaps itself and therefore interferes with itself either constructively or destructively.
In solving the Shroedinger equation of such systems, we see that time no longer intervenes in the form of the wave function and that it is only space (the position) which determines the shape of the wave.
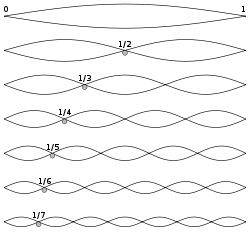
We are in the case of ondes_stationnaires_en that we have already mentioned.
That is to say that the places where the interferences are constructive, are always the same as the places where they are destructive.
The standing wave is a powerful concept that allows us to understand how a static phenomenon can come from a dynamic phenomenon.
This is one of the elements that allows the integration of the quantum vision: all the stability of the matter we experience comes from an entanglement of waves moving permanently but whose resultant by interference is stable.
For the atom, this gives well defined orbits whose shapes are provided by the solution functions of the Shroedinger equation, the atomic orbitals: the clouds are the clouds of probabilities of presence of the electron.
The denser the cloud, the greater the probability of presence of the electron.
Representation of the probability amplitude of standing waves (harmonics) of the harmonic oscillator.
Note the similarity with the vibration states (Vibration nodes and bellies) of a vibrating string.
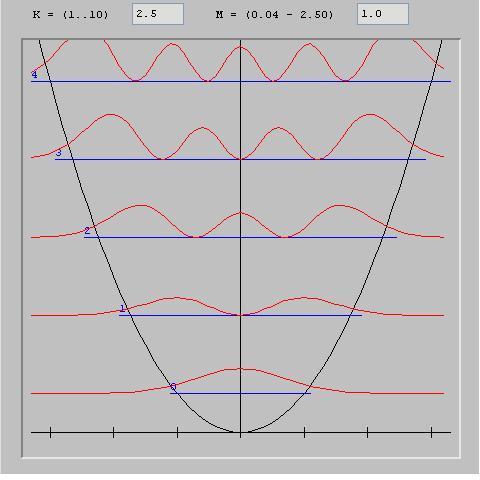
We notice that in the quantum case (to the left) the probability amplitude of the wave functions (in red) decreases progressively when moving away from the center, i.e. in the regions where the potential becomes stronger (parabolic curve in black) but is never totally null.
So we have chances during an observation to find the particle in a remote region where the potential energy is stronger than the kinetic energy while classically it would be trapped in the region where the potential is lower than its kinetic energy.
It is this fact that is at the origin of theeffet_tunnel which allows a quantum particle to cross a potential barrier whose energy is higher than the energy of the particle because the wave function is not zero on the other side of the barrier allowing the particle to be observed there.
We find here a consequence of the non-local aspect of the wave function.
This is the constraint that the energy imposes on the wave function to remain localized and thus to interfere with itself to produce standing waves associated with particular values of energy (quantified values therefore) which is at the origin of the concept of "quantification".
Finally, we have to talk about what is at the origin of the quantum theory: the constante_de_Planck which appears in the Shroedinger equation.
This constant was introduced by the physicist Max_Planck to explain the value of the thermal radiation of the material as a function of the temperature.
The observed law that this radiation follows forces us to consider that the thermal energy is not emitted continuously but by packet or "quanta".
It is the first evidence of the quantum character of matter.
In physics, action is defined as the product of energy and time.
It is quite intuitive: when an energy acts during a certain time it generates a certain action whose value is proportional to that of the energy and to the length of time during which it acts.
Planck's constant represents the smallest possible action in the physical world.
It is a universal constant of physics that characterizes the quantum nature of reality.
The value of this constant is extremely small: 6.62607004 × 10-34 m2 kg / s but it is nevertheless non-zero.
which are called Planck units.
Thus the physical world as described by quantum mechanics has a limit in the infinitely small beyond which we can no longer speak in terms of physics, it is finally an edge of the physical world.
If there is an edge, a limit, it is a natural quantum constraint for the wave function and therefore for the quantization (which is in itself, as we have seen, a strength).
The Planck constant defines the pixelation of the Universe.
We can also find the most fundamental origin of quantification in the functioning of the consciousness which by nature is not continuous.
Indeed, if we consider the observation by a subject of an object which is a point of view in the consciousness, this one is possible only by discrimination of the consciousness of the different possible points of view.
For them to be identified, the points of view must be distinct, otherwise all the points of view would merge and there would be no real observation.
Discrimination is the quality of the intellect which is in this sense a fundamental property of the consciousness.
We thus find the elements present in the quantum postulates of the measurement.
"
1.5.1.Analysis of the aphorism
poem quantum matching link to the postulates
What is the wave function or state vector or "ket" (from bracket , hook in French) . Premier postulat
possible the probabilistic structure of the wave function, the different possibilities eigenstates of the ket . Troisième postulat is accomplished the dynamics of the Hamiltonian operator total energy of the system responsible for the evolution. . Deuxième postulat under the eye of the conscience the postulates of the measurement, i.e. the necessary intervention of the observer . Quatrième postulat only what is possible is accomplished only the eigenvalues of the observable can be obtained and the state of the system is then the corresponding eigenstate. . Cinquième postulat What is possible is accomplished the Schrödinger equation, the quantum dynamics equation. . Sixième postulat
The great difficulty of scientists to accept the message of quantum theory explains why so few people can access it.
Here you will find a summary of this situation, analyzed by Jean Staune and reported by Bruno Lussato: bruno_lussato_les_plus_grandes_désinformations_de_l_histoire_des_sciences
(blog where I left a testimony in 2009 about the conference Alain Aspect gave in 1982 in Toulouse while he was touring France to present the results of his work.bruno lussato the greatest misinformation in the history of science nweb) This text could have been written and probably much better by a great number of informed people who are part of the scientific "establishment" but their reluctance to do so has led me on the one hand to be able to reserve the name of quantum domain.
org which was curiously available and on the other hand to spend tens of hours to work out this text which is probably still to be improved...
of a reality independent of space and time, that is to say of all
space-time contingencies, i.e. all physical contingencies.
The postulates obviously do not include the observer in the physical system
but declares its existence necessary for an observation to take place or for a
physical result is produced.
This is perfectly in line with the shamans' conceptions of the "dream of the world"..
The difference with reality is that the holographic simulation of the world is not made
by material computers but by a non-material cosmic computer which identifies itself
to the consciousness in its most extended conception.