De postulaten van de kwantummechanica
versie beschikbaar in : en it ru zh es ja de pt fr
datum aangemaakt : 20240129- datum van bijwerking : 20221007- généré le: 20241110_231431
Dit artikel presenteert in detail de postulats_de_la_mécanique_quantique vanuit eenvoudige wiskundige en geometrische overwegingen en analogieën uit het dagelijks leven....
In de natuurkunde worden begrippen ontwikkeld die verband houden met wiskundige objecten om theorieën op te stellen die het mogelijk maken de fysieke wereld weer te geven door middel van de werkingswetten..
De klassieke mechanica of de theorie van Newton is de theorie waarmee we de werking van materie kunnen weergeven op schalen die gevoelig zijn voor menselijke waarneming en die we macroscopisch noemen..
Op kosmologische schalen wordt deze theorie veralgemeend door Einsteins relativistische theorieën.
Algemene relativiteit is de theorie die het meest ingaat op de zwaartekracht....
De kwantummechanica is de theorie waarmee we de werking van de materie op microscopisch niveau kunnen weergeven, hoewel de grens tussen het microscopische en het macroscopische niet duidelijk is gedefinieerd in termen van schaal, zodat we kwantumgedrag kunnen hebben op macroscopische schalen, zoals in de laser of de cables_électriques_supraconducteurs De kwantumtheorie gaat niet over een bepaalde natuurkracht zoals de algemene relativiteit, het is meer een taal....
De taal van kwantumobjecten.
Zo kunnen we deze taal toepassen op verschillende krachten of systemen, en ze dus kwantificeren.
De reeks kwantumconcepten draait om zes basispostulaten die de kwantumtheorie volledig definiëren.nweb supergeleidende stroomkabels Wij zullen deze zes postulaten voorstellen en proberen hun betekenis op een eenvoudige manier vast te stellen.
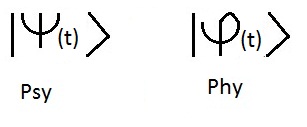
De uitdrukking van het eerste postulaat zoals gedefinieerd in Cohen-Tanoudji's boek " Quantum Mechanics Volume 1" is :
Op een vast tijdstip t wordt de toestand van een fysisch systeem gedefinieerd door de gegevens
van een ket of golffunctie of toestandsvector opgemerkt |psy(t)> die behoren tot de toestandsruimte ".
Postulaat I nweb
De Griekse letter Psy wordt gebruikt om de golffunctie aan te duiden, wij gebruiken
ook onverschillig de brief Phy.
Het eerste concept van de mechanica betreft de weergave van de toestand van het fysieke systeem.
Dit is een natuurlijke manier om het onderwerp van de studie te definiëren. Hier zeggen we gewoon dat het systeem bestaat
en dat de toestand ervan kan worden voorgesteld door een tijdsafhankelijke functie
Dit komt omdat de toestand van het systeem niet a priori statisch maar dynamisch is..
In de klassieke mechanica wordt het fysieke systeem voorgesteld door het "materiële punt"..
Een complex systeem wordt voorgesteld door een reeks verbonden materiële punten
tussen hen om een vast of niet vast object te vormen (stijve of niet-stijve verbindingen, bijv.: kristal of gas).
Het eerste postulaat stelt eenvoudig dat de toestand van het systeem op een bepaald tijdstip uniek is.
en behoort tot een verzameling van mogelijke toestanden gegroepeerd in een verzameling
wiskunde genaamd "staatsruimte"..
We spreken van ruimte en niet gewoon van een verzameling, omdat de kwantumtoestand een vector is...
dat is een wiskundig object dat een richting in een ruimte voorstelt.
We kennen allemaal de driedimensionale ruimte (lengte, breedte, hoogte of diepte, afhankelijk van de oriëntatie van de eerste twee dimensies)
Het is de fysieke ruimte waarin we leven.
De ruimte van toestanden waarin kwantumsystemen "leven" is geen fysieke ruimte, maar een abstracte ruimte. (Hilbertruimte)
en zijn dimensie is oneindig om de oneindigheid van mogelijke toestanden weer te geven die zelfs voor eenvoudige fysische systemen bestaan..
Laten we een analogie maken met een voorbeeld uit het dagelijks leven
om te begrijpen hoe een kwantumsysteem wordt gemodelleerd.
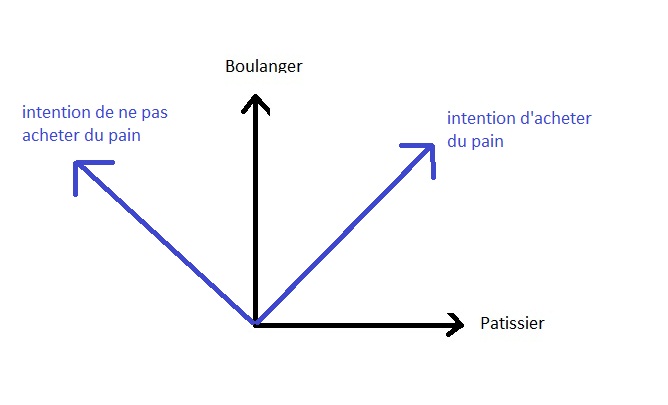
Stel je voor dat iemand rustig in zijn flat zit en plotseling...
beseft dat ze brood moet gaan kopen....
Ze maakt zich klaar om te vertrekken en in gedachten twijfelt ze nog over de plaats waar ze brood gaat kopen.
Ze heeft de keuze tussen een bakkerij verderop in de straat of een banketbakkerij die ook
die verderop in de straat van haar.
Als men de trap afloopt om naar buiten te gaan, kan men zeggen dat er twee toestanden zijn mogelijk in zijn hoofd die overeenkomen met de twee opties voor brood kopen. Deze opties kunnen op kwantitatieve wijze worden genoteerd:
staat 1: |bakker>
status 2: |banketbakkerij>
De gemoedstoestand van de persoon is een combinatie van deze twee mogelijkheden:
| Status> = |bakker> + |banketbakkerij>
De twee staten zijn volledig onverenigbaar: of ze koopt het brood bij de bakker of de banketbakker.... Beide mogelijkheden hebben niets gemeen, ze delen niets. Geometrisch worden ze orthogonaal genoemd. (loodrecht) en geometrische representatie in de ruimte (van de staten dus) zal:
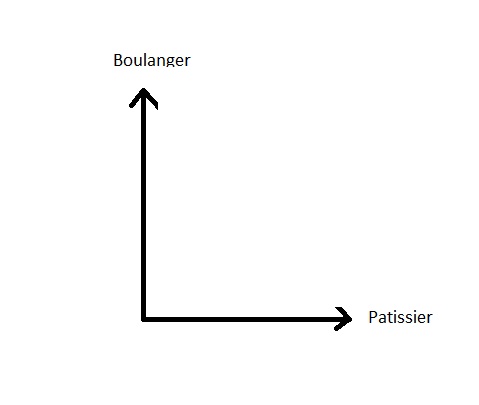
We hebben dus twee zeer verschillende richtingen die niets gemeen hebben.
Als de pijl (vector) Baker leunde naar de pijl (vector) banketbakkerij
dan zou dit betekenen dat gaan kopen van
de bakker is een beetje verbonden met gaan kopen
in de banketbakkerij, wat niet het geval is, het zijn twee
opties incompatibles: orthogonaal, d.w.z. onder een rechte hoek: ze delen niets in termen van leiderschap.
Anderzijds, de toestand van het systeem, d.w.z. de geestesgesteldheid...
van de persoon is een zogenaamde lineaire combinatie van de twee toestanden.
We zeggen dat we een mengsel van toestanden hebben. De echte gemengde staat is niet
komt niet overeen met iets waarneembaars: we weten het niet
niet waar het brood wordt gekocht.
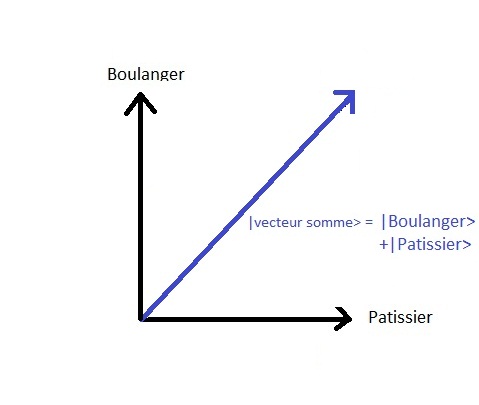
Deze lineaire combinatie van de twee mogelijkheden komt overeen met
aan de som van de twee vectoren die de waarneembare toestanden voorstellen.
De som van twee vectoren wordt als volgt gerealiseerd : dat doen we
Van het einde van de eerste vector en de tweede vector
som die voortvloeit uit het begin van de eerste en eindigt tegen het einde
van de tweede.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
De toestandsruimte zou een vectorruimte zijn, d.w.z. een ruimte van richtingen, dit betekent dat we in de geometrische voorstelling de vectoren kunnen verplaatsen zonder ze te veranderen natuur, blijven ze dezelfde vectoren: ze wijzen in dezelfde richting. Ook om te vereenvoudigen de voorstelling zijn alle vectoren vanuit hetzelfde punt vertrokken om aan te geven dat alleen richtingen bestaan in deze ruimte. Dit wordt een vectorruimte genoemd in tegenstelling tot naar een ruimte van punten die in de wiskunde een affiene ruimte wordt genoemd. ( Het scherm waarop die u nu leest is een voorbeeld van een affiene ruimte waar pixels punten in die ruimte voorstellen....staatssom vector img)
De geometrische voorstelling gebeurt uiteraard in een ruimte van punten, want een vectorruimte
is een pure abstractie en kan alleen worden weergegeven in de ruimte die wij waarnemen met punten (posities) verschillende.
Maar dit bestaat niet in de toestandsruimte waar alle representaties van een vector bij verschillende
posities in de representatieruimte corresponderen met één vector in de vectorruimte.
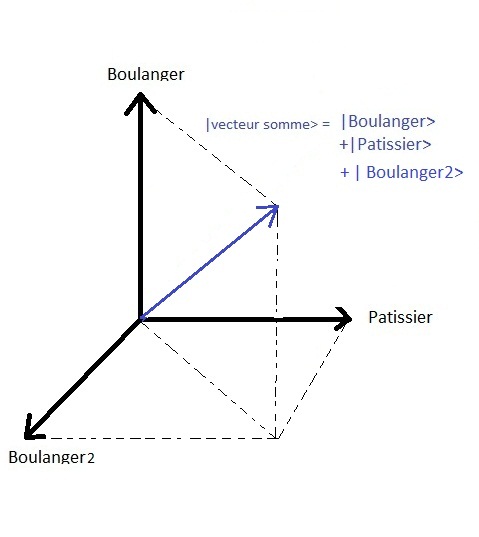
De toestand kan dus als volgt worden voorgesteld :
Hier is de dimensie van de toestandsruimte twee. Als er een derde optie was
met een andere bakker in een aangrenzende straat | bakker2 > dan zou de toestandsruimte van dimensie drie zijn, enz..
In de natuurkunde kunnen systemen met twee toestanden op dezelfde manier worden gemodelleerd.
Dit is het geval voor de geïoniseerde waterstofmolecule. De waterstofmolecule
is samengesteld uit twee waterstofkernen, d.w.z. twee protonen
en het feit dat het geïoniseerd is, betekent dat er een elektron uit verwijderd is...
van de twee bezit het natuurlijk. Bijvoorbeeld
omdat het eenvoudig is : " tot een enkel elektron ".
De twee mogelijke positietoestanden voor het elektron zijn :
De geometrische voorstelling is:
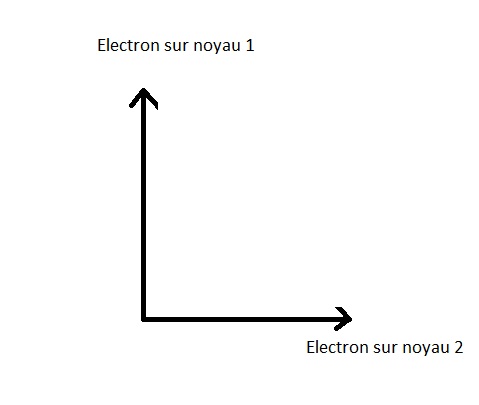
Het is duidelijk dat het elektron niet gevonden kan worden... (of liever gezegd te vinden, d.w.z. : worden waargenomen) op hetzelfde moment op kern 1 en kern 2, deze toestanden zijn orthogonaal.
In de uitdrukking van het postulaat worden synoniemen gebruikt om de toestandsvector aan te duiden, die onverschillig wordt genoemd
toestandsvector, golffunctie of ket. Deze verschillende namen komen overeen met verschillende wiskundige aspecten van de toestandsvector.
We zullen het aspect van de golffunctie zien in de uitleg van het tweede postulaat en het aspect van de "ket" in het derde..
Samengevat wordt de kwantumtoestand voorgesteld door een gegeven vector (richting) in een vectorruimte (van richtingen),
deze vector heet ^staatsvector "..
In de klassieke mechanica wordt de toestand voorgesteld door het "materiële punt" dat gedefinieerd wordt door zijn fysische eigenschappen.
positie en snelheid.
Het is belangrijk op te merken dat in de kwantummechanica de toestand van het systeem volledig onafhankelijk is van de toestand van het systeem.
de fysische eigenschappen van het systeem. De toestand wordt op een abstracte manier gedefinieerd en men zou kunnen zeggen "niet fysiek"..
Dit zal worden uitgewerkt in de presentatie van de volgende postulaten via het begrip "staatsvectorrepresentatiebasis"..
Maar het eerste postulaat maakt de toestandsvector alleen afhankelijk van de tijd en niet van de positie.
dat is de ruimte. Dit betekent dat de golffunctie niet-lokaal is....
Uiteraard leert de relativiteit ons dat tijd en ruimte een continuüm vormen en dus als een formulering van
kwantummechanica ten minste rekening houdt met speciale relativiteit, hangt de toestandsvector niet af van
van tijd. Deze theorie is de kwantumelektrodynamica of kwantumtheorie van het elektromagnetische veld.
De speciale relativiteit is nauw verbonden met het elektromagnetisme doordat Einstein deze theorie heeft opgesteld.
om de paradoxen weg te nemen die Maxwells elektromagnetische theorie opriep....
Kwantumconcepten werden niet door pure verbeelding bedacht. Ze zijn veeleer gesmeed in het vuur van het experiment...
van de microfysica die deze concepten goed weergaven....
Hoewel volledig abstract, is de kwantumtoestand toch echt....
Deze realiteit van de kwantumtoestand blijft vaak het moeilijkst toe te geven, ook al is het onvermijdelijk..
De werking van materie, het meest concrete, wordt beheerst door iets totaal abstracts....
Toch is het onmogelijk om deze moeilijkheid te omzeilen, want dit kwantumconcept is buitengewoon solide.
De cognitieve situatie is enigszins vergelijkbaar met de ontdekking van elektromagnetische golven. Deze golven werden eerst theoretisch
ontdekt door het combineren van Maxwells vergelijkingen die elektrische en magnetische velden beschrijven.
Hun combinatie leverde een golfpropagatievergelijking op met een constante snelheid. Het was een abstract begrip
en nieuw, maar experimenten hebben aangetoond dat elektrische en magnetische velden golven produceren...
die gecontroleerd en gebruikt konden worden, wat leidde tot radiocommunicatie....
Wij hebben gezien dat deze snelheid de gemeten lichtsnelheid is....
Op dezelfde manier is het zeer abstracte concept van een golffunctie zeer concreet geworden inintrication_quantique en gaf aanleiding tot het technologiegebied van cryptographie_quantique
Postulat_II
"Elke waarneembare fysische grootheid \"a\" wordt beschreven door een operator \"A\" die handelt in de toestandsruimte; deze operator is een waarneembaar.
" In de klassieke mechanica hebben we gezien dat het de eigenschappen van het materiële punt, zijn snelheid en zijn positie zijn die de toestand bepalen..
Bijvoorbeeld de snelheid en positie van een bal op een tennisbaan of van een planeet in het zonnestelsel..
De positie en snelheid van een macroscopisch voorwerp worden op elk moment bepaald en dit bepaalt volledig de toestand van het systeem..
De evolutie van de tennisbal in de ruimte bepaalt op elk moment de toestand van het spel, of de bal in beweging is, "out" of niet of onbeweeglijk op de grond na het net te hebben gevangen..
En het is de geschiedenis van de staten die de wedstrijd en de uitkomst bepaalt....
Anderzijds wordt in de kwantummechanica de algemene toestand van een tot een deeltje gereduceerd systeem, zoals het elektron in het vorige voorbeeld, niet langer geassocieerd met een bepaalde positie of snelheid, maar met een mengsel van alle mogelijke posities of snelheden..
Bovendien kunnen we niet alle eigenschappen van het systeem tegelijk waarnemen, zoals in de klassieke mechanica.
Als het systeem in een positiestaat is, is het niet in een energietoestand en omgekeerd..
In het voorbeeld van het brood hebben we positietoestanden, namelijk de bakker en de banketbakker, die aangeven waar het brood is gekocht, maar zoals we zullen zien zijn dat geen energietoestanden..
Net als in het voorbeeld van het waterstofmolecuul vertegenwoordigt het feit dat het elektron zich op kern 1 of kern 2 bevindt positietoestanden, maar die zijn op zichzelf geen energietoestanden van het molecuul..
In een kwantumsysteem delen de verschillende eigenschappen dezelfde toestandsruimte, maar de toestanden die overeenkomen met de verschillende eigenschappen worden niet noodzakelijkerwijs vertegenwoordigd door dezelfde richtingen in de ruimte..
Dit betekent dat als de ruimte tweedimensionaal is, er twee mogelijke positiestaten zijn maar ook twee mogelijke energiestaten en dat de energiestaten niet dezelfde richtingen hebben als de positiestaten..
In het geval van de waterstofmolecule (geïoniseerd) zijn de mogelijke energietoestanden:
| Status:energie> = |verwante staat> |niet-gebonden staat>
in de "dynamische of energie" voorstelling van het waterstofmolecuul....
De algemene toestand van het systeem is volledig onafhankelijk van zijn eigenschappen, dus voor brood kunnen we schrijven:
| Status> = |bepaling> |afstand doen> = |bakker> |bakker>
Voor de waterstofmolecule die El (verwante staat) en Enl (niet-gebonden staat) de energietoestanden en P1 en P2 de positietoestanden, hebben we:
| Status> = | De > | Enl > = | P1 > | P2 >
Het feit dat de toestand onafhankelijk is van zijn waarneembare eigenschappen en onafhankelijk daarvan kan worden uitgedrukt, is een fundamenteel kenmerk van de kwantummechanica..
De eigenschappen worden voorgesteld door wiskundige operatoren die, wanneer zij worden toegepast op de kwantumtoestand, de mogelijke toestanden voor die eigenschap bepalen..
Een operator in de wiskunde is wat een waarde doet evolueren in de ruime zin.
Bijvoorbeeld voor optelling geeft de operator "3 " toegepast op "2" "3 2".="5" we veranderden de waarde van "2" in "5" door de operator "3 " toe te passen. (toevoeging van de waarde drie) In de kwantummechanica laat de operator de toestand evolueren....
Het postulaat zegt dat de operator " werkt " op de toestandsruimte.
Zij P de positie-operator en E de energie-operator (in werkelijkheid wordt de energie-operator aangeduid met H voor hamiltonien_nl die de totale energiefunctie is die in de algemene mechanica door Hamilton is gedefinieerd als de som van alle energieën die op het systeem inwerken).
Volgens het tweede postulaat vertegenwoordigen deze operatoren de overeenkomstige eigenschappen (positie en energie) van het systeem.
Door het toepassen van (het laten werken) de positie operator op de toestand van het waterstofmolecuul hebben we:
P | status > = | P1 > of P | status > = | P2 >.
Het toepassen van de operator op de toestand betekent het observeren van de eigenschap die met de operator overeenkomt, hier de positie.
Op dezelfde manier met de energie-operator.
H | status > = | De > of H | status > = | Enl >.
We zien dat wanneer we een operator op een toestand toepassen, we deze toestand laten evolueren naar een toestand die bij deze specifieke operator hoort, we noemen deze toestand "schone staat " van de operator.
Het resultaat kan elke mogelijke toestand zijn voor het systeem en voor de exploitant. (de gemeten eigenschap).
De staat "gebonden molecuul " is een eigen toestand van de energie-operator, terwijl de "electron op de kern 1" is een eigen toestand van de operator positie.
Voor het waterstofmolecuul in de gebonden toestand bevindt het elektron zich in een onbepaalde positie tussen de twee waterstofkernen..
De energie-eigenstaat kan worden beschouwd als een lineaire combinatie van positietoestanden, die kan worden voorgesteld als:
| De > = | P1 > | P2 >
Van de twee positietoestanden kan worden gezegd dat ze optellen tot een energietoestand: wanneer het elektron door de twee kernen wordt gedeeld, is het molecuul gebonden, de twee positiestaten zouden constructief interfereren om de "gebonden" energietoestand te vormen..
op dezelfde manier wordt de ongebonden toestand voorgesteld door | Enl > = | P1 >- | P2 >
de twee positiestaten zouden destructief interfereren om de energietoestand "ongebonden" te creëren..
Als we de broodanalogie opnieuw nemen, is de gemoedstoestand van de persoon een aarzeling tussen brood kopen bij de bakker of de banketbakker, maar ook tussen brood kopen of geen brood kopen.
Men kan zeggen dat de vastberadenheid om brood te gaan kopen een interférence_nl van alle mogelijkheden om brood te gaan kopen, terwijl afzien een interférence_nl destructief van deze zelfde mogelijke staten.
Wij beschouwen alle mogelijkheden die met het systeem kunnen gebeuren en die alle zijn opgenomen in de toestandsruimte.
Geometrisch kan dit als volgt worden voorgesteld:
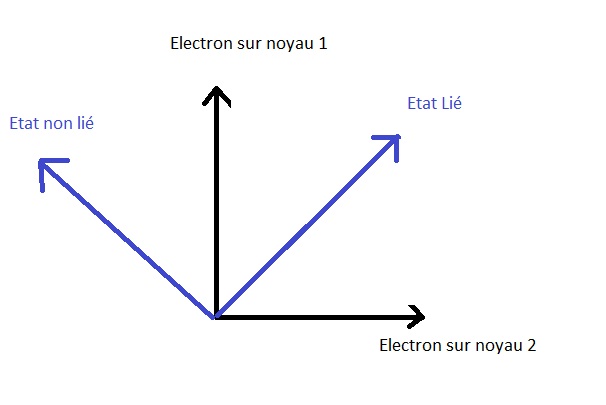
Het is te zien dat de waarneembare energietoestanden (gebonden of ongebonden staten van het molecuul) zijn ook orthogonaal omdat ze overeenkomen met mogelijke energieopties die niet met elkaar verenigbaar zijn.
De toestand van het systeem (toestandsvector) is zelf onafhankelijk van zijn voorstelling in de toestandsruimte met betrekking tot energie of positie.
De eigenstaten die bij een operator horen, vormen een basis om de toestandsvector voor te stellen. (hier blauwe of zwarte basis) Voor de toestandsvector hebben we dus een representatiebasis voor de positie-operator en een andere representatiebasis voor de energie-operator.
1.1.2.Principe d incertitude de Heisenberg
De principe_d_incertitude_de_Heisenberg volgt rechtstreeks uit de postulaten van de kwantummechanica.
Wij hebben gezien dat in het algemeen de eigenwaarden van twee observabelen niet door dezelfde vectoren worden weergegeven en dat bijvoorbeeld een energietoestand zal worden weergegeven door een lineaire combinatie (superpositie) van positiestaten.
In dit geval is het duidelijk dat het onmogelijk is om tijdens dezelfde meting zowel de positie-eigenschap als de energie-eigenschap van een systeem waar te nemen, aangezien hun eigenwaarden onverenigbaar zijn..
Wiskundig zeggen we dat de operatoren niet wisselen.
Dit betekent dat als de twee operatoren achtereenvolgens in een andere volgorde op het systeem worden toegepast, de uiteindelijke toestand anders zal zijn..
In de praktijk wordt in een kwantumexperiment een groot aantal deeltjes waargenomen, wat een globaal statistisch resultaat oplevert waarbij blijkt dat hoe nauwkeuriger de energiewaarde, hoe minder nauwkeurig de positie en omgekeerd..
1.1.3.Weergave van de golffunctie in de fysieke ruimte
Het verschil tussen de toestandsvector en de golffunctie is dat de toestandsvector onafhankelijk is van de fysieke ruimte, terwijl de golffunctie dat niet is, omdat hij zich in de fysieke ruimte voortplant..
In de kwantummechanica is de golffunctie een projectie van de toestandsvector in de fysieke ruimte..
In de onderstaande afbeelding hebben wij het golfaspect weergegeven (golffunctie) van kwantumtoestanden
visualiseren hoe de golf destructief of constructief interfereert door optellen of aftrekken.
De fundamentele werking van een golf is hetzelfde, of het nu een kwantumgolf is, een
elektromagnetisch of bijvoorbeeld een golf op het oppervlak van een waterlichaam (vaguelettes).
Een golf heeft altijd een trog en een piek trilling (van de golf) rond een gemiddelde waarde (het platte oppervlak van het water).
De pluspunten tellen op (evenals de minste) en de plussen en minnen trekken elkaar af en heffen elkaar op....
Bijvoorbeeld, als een golftrog de piek van een andere golf ontmoet, heffen de twee elkaar op en blijft over
het vlakke wateroppervlak op het overlappingspunt.
1.1.3.1.Waterstofmolecuultoestanden
De golftoestanden van een atoom of molecuul komen overeen met ondes_stationnaires_nl
dat zijn golven die zich niet voortplanten maar voornamelijk gelokaliseerd blijven in een beperkt gebied
van de ruimte, hier rond de waterstofkernen....
Het tweede postulaat introduceert dus de operatoren die op de toestanden worden toegepast om ze te transformeren.
We kunnen dus zeggen dat de toestandsvector het statische aspect van de kwantumwerkelijkheid vertegenwoordigt, terwijl de operator het dynamische aspect van diezelfde werkelijkheid vertegenwoordigt..
De derde, vierde en vijfde postulaat beschrijven het proces zelf van het waarnemen van een kwantumsysteem.
Postulat_III
Maatregel : mogelijke waarden van een waarneembaar " De meting van een fysische grootheid A kan alleen een eigenwaarde van de corresponderende waarneembaar A geven uit alle mogelijke waarden..
" We hebben gezien dat de waarneembare toestanden van een eigenschap van een kwantumsysteem "eigenstaten" worden genoemd. (van deze waarneembare).
Elke ^eigenstaat" heeft een bijbehorende ^eigenwaarde" die het resultaat is van de meting..
Voor het waterstofmolecuul bijvoorbeeld is het energieniveau van het molecuul verschillend als het molecuul in gebonden of ongebonden toestand is..
In de broodanalogie kan men zich voorstellen dat het resultaat de verandering is van het geldbedrag in de portemonnee dat is afgenomen toen het brood werd gekocht..
De eigenwaarde is een getal en de eigen toestand is, zoals we hebben gezien, een vector.
Tot dusver hebben wij alleen de richting van de vector gebruikt, die ook geassocieerd is met een dimensie van de toestandsruimte, aangezien dit het belangrijkste begrip is met betrekking tot de kwantumtoestand.
In de wiskunde is de natuurlijke waarde van een vector zijn lengte.
Deze lengte is abstract (het is geen fysieke ruimte dus het wordt niet gemeten in meters).
Daarom is een meer algemene term gecreëerd die verwijst naar lengte of schaal, vandaar de naam "scalaire waarde"..
De scalair is dus de numerieke waarde die hoort bij de lengte van een vector.
Als we de lengte van een vector vermenigvuldigen met een getal, krijgen we een vector waarvan de lengte een veelvoud is van de oorspronkelijke waarde, hij zal op een andere schaal staan, zijn nieuwe waarde "scalair"..
Hier observeren wij dus de energie van het systeem met behulp van de energieoperator.
Wij hebben gezien dat in dit geval de toepassing van de energieoperator op de toestand de twee mogelijke energietoestanden tegelijkertijd oplevert:
H toegepast op de | status > zal ofwel de staat | De > (naar link) geassocieerd met de energie El is de toestand | Enl > (voor niet-verwante) geassocieerd met de energie Enl (de energieën zijn de eigenwaarden van de energie-operator).
De logische operator "or" (of niet-exclusief) wordt in de kwantummechanica voorgesteld in de toestandsruimte door de optelling van de genoteerde vectoren " "..
We hebben dus:
H | status > = De | De > Enl | Enl >
De globale toestand is een superpositie van de mogelijke eigen toestanden waarbij El en Enl, zoals we hebben gezien, respectievelijk de energiewaarden van de twee toestanden voorstellen..
Om aan te geven dat tijdens een meting slechts één waarde mogelijk is, gebruiken wij een eigenschap van vectoren die projectie heet.
Hieronder staat de afbeelding van de globale staatsprojectie |Psy> op de energietoestand "gebonden molecuul". | De >
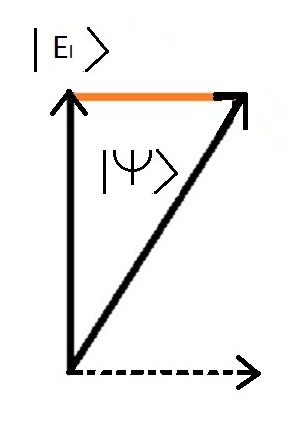Wanneer de fysische eigenschap aan het systeem wordt gemeten, is het postulaat dat de meting een unieke waarde oplevert en dat deze waarde overeenkomt met een bepaalde toestand van het systeem, ^eigenstaat" genaamd, waarbij de verkregen waarde ^eigenwaarde" wordt genoemd..
In de vorige vergelijking tellen we mogelijkheden op en geen waarden, zodat we geen E = Enl, het toevoegen van een vector werkt niet zoals het toevoegen van een waarde (scalair).
We zullen later zien dat het optellen van de mogelijkheden niet leidt tot de som van de energieën, maar tot de gemiddelde waarde van de energie, die de som is van de waarden (ici El Enl) gedeeld door het aantal toegevoegde waarden (2).
De gemiddelde energiewaarde zou dus E = (El Enl)/2.
In werkelijkheid is het iets subtieler dan dat, omdat de gemiddelde waarde van energie ook afhangt van de waarschijnlijkheid van het bestaan van elke energietoestand, dus is het een gemiddelde waarde gewogen met de waarschijnlijkheid van elke toestand.
Dit is precies het onderwerp van het vierde postulaat.
Postulat_IV
Geboren postulaat : probabilistische interpretatie van de golffunctie "Bij het meten van de fysische grootheid A aan een systeem in de genormaliseerde toestand "phi", is de waarschijnlijkheid P (Een) om de eigenwaarde An van de overeenkomstige waarnemer A te verkrijgen is |Cn|².
Waarbij Cn de amplitude is van de golffunctie geprojecteerd op de eigen toestand |phi n> die overeenkomt met de waargenomen eigenwaarde An.
Tot dusver hebben we het alleen gehad over toestanden, waarneembare eigen toestanden en de bijbehorende eigenwaarden..
Volgens afspraak is de lengte van een toestandsvector 1, omdat de toestandsvector het bestaan van het systeem weergeeft. (eerste aanname) en dat in termen van waarschijnlijkheid, de bevestiging van het bestaan van het systeem overeenkomt met een zekerheid.
In waarschijnlijkheid is de zekerheid 1.
Als je een kans van 1 op 1 hebt op iets... (1 gedeeld door 1 is 1) we zijn in de zekerheid.
Een waarschijnlijkheid van minder dan 1 is minder zeker dan volledige zekerheid.
Bijvoorbeeld, de kans om de loterij te winnen door slechts één rooster te spelen is 1 gedeeld door een paar miljoen.
Dit betekent dat uiteindelijk slechts één of bijna één de miljoenen zal winnen bij de trekking ! De loting in kwantumtermen is "de waarneming van de winnaar "..
De amplitude van de golffunctie is gelijk aan de lengte van de toestandsvector.
We hebben gezien dat een scalair een eenvoudige numerieke waarde is.
Deze aanduiding verschijnt ook in vergelijking met complexere numerieke waarden die uit meerdere getallen bestaan, zoals de vector die, wanneer hij numeriek wordt weergegeven, het gebruik van meerdere getallen vereist.
(als we deze lijn van ontwikkeling volgen komen we uit bij het concept van "tensor" zeer gebruikt in de fysica, tensor van elasticiteit, van kromming van ruimte-tijd......Postulaat IV nweb).
_
Bij de projectie van een vector op een andere is de lengte die van de eerste naar de tweede wordt overgedragen een getal.
We hebben dus een bewerking uitgevoerd die een getal aan twee vectoren koppelt, die we scalair noemen om aan te geven dat het specifieke resultaat van deze bewerking van twee vectoren geen derde vector oplevert zoals bij het optellen van vectoren, maar een getal (scalair).
Deze bewerking heet het scalair product: Het scalair product is een bewerking die uit twee vectoren een getal geeft.
Dit getal is de orthogonaal geprojecteerde lengte van de ene vector op de andere.
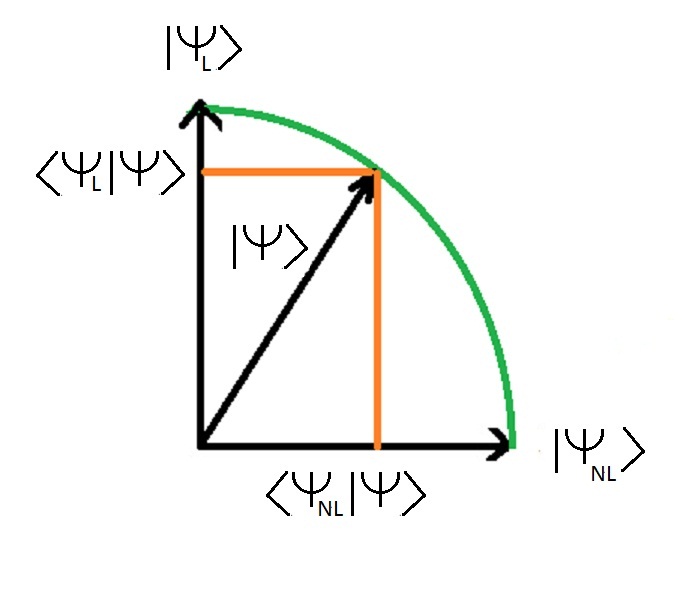
Het Engelse woord "bracket" verwijst naar de tekens ".<" et ">" Deze haakjes worden traditioneel in de wiskunde gebruikt om de gemiddelde waarde van een grootheid weer te geven.. De onderstaande afbeelding toont de projectie van de algemene toestand | Honden > op de twee energietoestanden | Honden l > en | Honden nl > (die hetzelfde zijn als de staten | De > en | Enl > het is gewoon een verschil in notatie)
Toen we de staten "brood kopen" in aanmerking namen |bakker> en |bakker> hebben wij impliciet aangenomen dat wij het ene en het andere onverschillig kunnen waarnemen, d.w.z. met een gelijke waarschijnlijkheid van voorkomen.
" De som van het kwadraat van de lengten van de twee zijden is gelijk aan het kwadraat van de lengte van de schuine zijde " In ons geval komt de hypotenusa overeen met de toestandsvector |phi> en beide zijden aan de |phi> op de twee eigenstaten |bakker> en | Epicier>. Als we de uitdrukking | Honden L >< Honden L | bestaande uit een ket en een beha en toegepast op de ket | Honden > verkrijgen we | Honden L >< Honden L | Honden > waarbij < Honden L | Honden > is de waarschijnlijkheidsamplitude van het verkrijgen van de toestand | Honden L > dus we hebben : | Honden L >< Honden L | Honden > = | Honden L > Al = Al | Honden L > zien we dat de eindtoestand de | Honden L > geassocieerd met de kans Al De uitdrukking | Honden L >< Honden L | is dus een operator die de begintoestand heeft veranderd | Honden > naar de uiteindelijke staat | Honden L > en dit met een waarschijnlijkheid Al.
1.2.2.Scheidingswand van de eenheid
Beschouw de volgende operator:
| Honden L >< Honden L | | Honden nl >< Honden nl | die de som is van de evolutie operatoren naar de eigenstaten van een waarneembaar (hier de energie : gebonden en ongebonden staat).
Het is interessant op te merken hoe de vectorrepresentatie van de toestand en de ontbinding ervan volgens een orthogonale basis het mogelijk maakt op natuurlijke wijze de amplitudes van de waarschijnlijkheden en dus de waarschijnlijkheden van de evolutie van het systeem tijdens een meting weer te geven..
Postulat_V
Maatregel : golfpakketreductie Als de meting van de fysische grootheid A, op tijdstip t, op een systeem voorgesteld door de vector |phi> resulteert in de eigenwaarde An dan wordt de toestand van het systeem onmiddellijk na de meting geprojecteerd op de eigenspatie die hoort bij An Dit postulaat wordt ook wel "wave packet reduction postulaat" genoemd..
Het is waarschijnlijk de grootste conceptuele revolutie van de kwantummechanica om het feit te introduceren dat de waarneming van het systeem ervoor zorgt dat het evolueert, terwijl in niet-kwantumfysische theorieën alleen de dynamische vergelijking verantwoordelijk is voor de evolutie van het systeem..
Traditioneel drukt de dynamische vergelijking van een mechanische theorie uit hoe energie op het systeem inwerkt om het te transformeren..
L_expérience_du_chat_de_Shroedinger is een gedachte-experiment bedacht door de natuurkundige Erwin_Shroedinger nadenken over het probleem van meting in de kwantummechanica dat rechtstreeks verband houdt met het vijfde postulaat.
Let op het verband tussen de waarnemer en de golffunctie: geen van beide is materieel ! Men zou kunnen zeggen dat wat materieel is, datgene is wat tussen de twee ligt: observatie.
De golffunctie en het bewustzijn vertegenwoordigen twee kanten van dezelfde werkelijkheid die de materialiteit overstijgt en
aan de oorsprong van deze materialiteit.
Uiteraard gaan natuurkundigen in het algemeen niet zo ver in hun kijk op de kwantumwerkelijkheid....
De standaardpositie op dit gebied is deinterprétation_de_l_école_de_Copenhague.
Dit standpunt komt voort uit de situatie van de menselijke waarnemer die een klassieke wereld ervaart en deze als de absolute referentie beschouwt.
Er kunnen verschillende graden van afstand tot deze positie worden gedefinieerd:
Er zij op gewezen dat dit standpunt wetenschappelijk niet langer houdbaar is sinds het experiment van Aspect, dat de mechanica valideert
in zijn meest verontrustende verklaringen.
Tegelijkertijd is deze kwantummechanica de meest geverifieerde theorie in de geschiedenis van de wetenschap....
Dit standpunt wordt dus gereduceerd tot een eenvoudig "materialistisch geloof"..
Dit was nochtans de mening van Einstein, maar helaas leefde hij niet lang genoeg om
zie de oplossing van de paradox die hij samen met de natuurkundigen Podolsky en Rosen in zijn beroemde artikel heeft gedefinieerd, door het Aspect-experiment.:
de Paradoxe_EPR.
Hier vertegenwoordigt de klassieke wereld waarin wij leven niet langer de totaliteit van de wereld omdat er...
een absoluut vreemde kwantumwereld waartoe we geen toegang hebben, maar waarmee we kunnen omgaan door
via de kwantumtheorie.
De stabiele fysieke wereld die wij kennen bestaat uit slechts drie kwantumdeeltjes: elektron, proton en neutrino.
Dit derde gezichtspunt neemt alle kwantumparadoxen weg door, eindelijk en eenvoudig, te zeggen dat we niet moeten
niet streven naar een interpretatie (klassiek) van de kwantumtheorie, maar dat men het gewoon moet accepteren...
Er kan dus worden voorspeld dat het kwantummodel nooit fout zal zijn.... Sinds het begin is het steeds duidelijker geworden hoe de kwantumwerkelijkheid
intervenieert in het begrip van de wereld om ons heen en meer in het bijzonder op het gebied van het leven, een macroscopisch systeem van grote samenhang... kwantum.
Twee vrij recente voorbeelden zijn:
Postulat_VI temporele evolutie van de kwantumtoestand. _ H |Phi(t)> = i h/2*pi d |Phi(t)> / dt _
0,000000000000000000000000000000000662607004 Wanneer deze constante wordt gecombineerd met andere fundamentele constanten zoals de lichtsnelheid of de universele gravitatieconstante, kunnen de minimumhoeveelheden van de verschillende eenheden van de natuurkunde worden afgeleid : Planck lengte, Planck tijd, enz....
1.5.Gecomprimeerde poëtische uitdrukking van postulaten
Het volgende is een poging om alle veronderstellingen in één aforisme samen te brengen:
"Wat mogelijk is wordt volbracht, onder het oog van het geweten, alleen wat mogelijk is wordt volbracht.
De kwantummechanica is de grootste revolutie van ons moderne wetenschappelijke tijdperk, omdat zij het materialistische standpunt definitief vernietigt en aldus de weg opent naar een ontwikkeling van de mensheid waarin wetenschap en bewustzijn weer verenigd zullen worden..
Het beslissende experiment waarmee de paradox Einstein-Podolski-Rosen kon worden opgelost, in 1982 uitgevoerd door onderzoeker en experimentator Alain Aspect
in het Orsay centrum voor kwantumoptica was gebaseerd op fotonen.
Een gedetailleerde beschrijving van de onderliggende theorie is te vinden in
Bernard d'Espagnat's boek " A la recherche du réel". .
Datzelfde jaar zat ik op de universiteit en Alain Aspect was...
kwam zijn resultaten presenteren in Toulouse, in het Maxwell amfitheater van de Universiteit
Paul Sabatier.
Het amfitheater bestond uit drie traveeën, gescheiden door twee trappen.. De
De grootste centrale hal was gevuld met natuurkundigen en andere
wetenschappers van de hele Rangueil-campus. Op de andere banken was er niemand... ! Het was
erg nieuwsgierig omdat degenen achterin de zaal konden zien...
minder goed dan wanneer ze dichter bij elkaar waren gekomen op de zijvleugels. Cel
Ik was geamuseerd omdat ik wist waarom het zo was, maar het was toen
zelfs indrukwekkend. Wat hen zou worden aangekondigd, zou als een slag op het hoofd zijn....
Na het presenteren van ondubbelzinnige meetresultaten, heeft hij
liet de vergadering sprakeloos achter (zat de collegezaal vol met professoren en studenten.
van onderzoekers) .
Aan het einde van de presentatie, na een lang moment van stilte,
significant toen het woord werd gegeven aan een vergadering van wetenschappers, een
onderzoeker stond op (mijn toenmalige relativiteitsleraar Alain Gautier...) en stelde
deze vraag:
" En je vindt het makkelijk om daar nu mee te leven? " .
Aspect, in de verdediging, antwoordde dat hij dat niet had gezegd, dat hij had gedaan
een experiment en dat het resultaat dat was, maar dat hij voorzichtig was niet te
een interpretatie geven.
Ik hoorde jaren later van iemand die bij hem was geweest dat hij
pro-Einsteiniaans was en dat hij verwachtte dat de kwantummechanica...
zou falen.
Ik zat op een zijgang in de derde rij, helemaal alleen en ik was...
Ik was geamuseerd omdat ik echt niet begreep waarom ze er een probleem mee hadden, of waarom ze niet wisten wat ze moesten doen.
ik begreep het maar al te goed.
Toen het experiment zich in een vroeg stadium bevond en het resultaat niet duidelijk was, werd de
meer dan een kwestie van tijd, de controverse is zeer sterk geworden, zelfs zwavelachtig.
Ik had een artikel gezien in het populaire tijdschrift Science
die een tegenexperiment presenteerde voor het experiment van Aspect, uitgevoerd door een Italiaanse natuurkundige...
die zei dat als het Aspect experiment de kwantummechanica zou bevestigen dan
zou hij stoppen met zijn studie natuurkunde omdat het voor hem geen zin meer heeft.... Ik weet niet of hij
hield zijn woord.
Toen de wetenschappelijke gemeenschap van natuurkundigen in shock was,
kon men zich afvragen wat er ging gebeuren.
Het kostte tijd om de informatie te verwerken, zoals te zien is in
2020 dat de situatie aanzienlijk is veranderd, kijk maar naar
Deze conferentie werd gegeven aan de Ecole Polytechnique door Hervé Zwirn, directeur van
onderzoek bij het CNRS
_x_sciences_de_l_homme_et_de_la_société_x_shs_mécanique_quantique_le_monde_existe_t_il
Deze ervaring heeft (of had moeten hebben voor de meerderheid) dezelfde soort
effect in de natuurkundige gemeenschap dat de ontdekking van de
ondes hertziennes (elektromagnetische golven) die het abstracte concept van
elektromagnetisch veld een veel levendigere realiteit.... De ontdekking van de
niet-scheidbaarheid en de observatie ervan op fysisch niveau geeft leven aan het concept van
onafhankelijke werkelijkheid, d.w.z. een werkelijkheid die onafhankelijk is van ruimte en tijd, d.w.z.
Een eerste conclusie die kan worden getrokken uit het eerste postulaat van
kwantummechanica is dat:
De realiteit van een kwantumsysteem (en uiteindelijk zijn alle systemen kwantum...! )
is gebaseerd op een abstracte ruimte van mogelijkheden die op zichzelf niet waarneembaar is... (
niet-fysiek en onafhankelijk van alle ruimte-tijd omstandigheden) meer
niettemin reëel, aangezien het vanuit dit niveau van abstract functioneren is dat de
de concrete werkelijkheid (waargenomen) .
Om het in één woord samen te vatten: het gaat over alomtegenwoordigheid en alwetendheid...
Voor de volledigheid wordt dit bovendien gerelateerd aan de waarnemer die niet
kan natuurlijk fysiek zijn. De veronderstellingen omvatten uiteraard niet de waarnemer
in het fysieke systeem, maar verklaart het bestaan ervan noodzakelijk voor
een waarneming plaatsvindt of een fysiek resultaat wordt geproduceerd.
Het is duidelijk dat de waarnemer en de
onafhankelijke realiteit hebben een nauwe relatie: ze zijn allebei niet-fysiek
en interageren in termen van informatie, kennis, perceptie.... Deze
past perfect bij de opvatting van de sjamanen over de " droom van de wereld"..
In dit opzicht kan de film Matrix worden gezien als een allegorie van
kwantumwerkelijkheid. Het verschil met de werkelijkheid is dat de
holografische simulatie van de wereld wordt niet gemaakt door hardware computers maar door
een niet-materiële kosmische computer die zich identificeert met het bewustzijn in zijn
meest uitgebreide ontwerp.
We kunnen en hebben dit universele bewustzijn alle
namen als men wil, maar deze zullen nooit de oneindige kracht van
dit bewustzijn.
De gemiddelde waarde van de energie wordt bijvoorbeeld genoteerd < E >.
We hebben gezien dat de kwantumtoestand ook wel "ket" wordt genoemd. | ket > het andere deel van de haakjes is de "bra" die een bepaalde operator is, genoteerd... < BH | Het is de natuurkundige Paul_Dirac die aan de oorsprong ligt van deze scheiding in twee van dit woord om een dynamiek van operator en vector te laten verschijnen in de operatie van het nemen van de gemiddelde waarde.
Als we de "bra" toepassen op de "ket" krijgen we < BH | ket > dat is het getal dat resulteert uit de toepassing van de operator
Hier hebben we een dubbele relatie tussen bh en ket.
Voor een staat (ou ket) "| Honden >^ le bra sera "< Honden |" de dualiteit tussen de twee wordt voorgesteld als het beeld in een spiegel De ket is een vector terwijl de BH een operator is, toepassing van de BH op de ket geeft een getal..
In het algemeen is in een uitdrukking wat rechts van de ket staat een operator, het resultaat van een operator op een toestand (vector) is ofwel een andere staat (vector) ofwel een getal dat een meetresultaat of een waarschijnlijkheid weergeeft.
Voor elke ket is er een overeenkomstige bh en de operatie die het mogelijk maakt om van de ket naar de bh te gaan heet hermitische vervoeging en wordt aangeduid met een sterretje.
Dus ( | Honden > ) * = < Honden | of (
Dit kan analoog worden gerelateerd aan een Vedisch aforisme waarin de schepper van het universum spreekt: " in mezelf gekeerd, creëer ik opnieuw en opnieuw ".
Dezelfde vorm is ook te zien in het eerste scheppingsverhaal in Genesis: laat er licht zijn en er was licht en D.
God zag dat het licht goed was.
< laat er licht zijn | en het licht was > = en D.
God zag dat het licht goed was.
< of | licht². | vat > = D.
God zag dat het licht goed was.
Het feit dat D.
God zag dat het licht goed was is duidelijk het resultaat van een waarneming.
We zouden dit alles het kwantumalfabet en de syntaxis kunnen noemen....
Het alfabet bestaat slechts uit één letter | Honden > en dat is "het wezen". (of de staat die de bevestiging is van het zijn...) De dubbele operatie * toont zijn dynamische operatorwaarde ( | Honden > )* = < Honden | Al hun combinaties leiden tot de kwantumgrammatica.
Een voorbeeld is de toepassing van de operator < Honden | over de staat | Honden > geeft < Psy|Honden > die ook de projectie is van de |Psy> op zichzelf en is daarom 1.
Dit kan triviaal worden vertaald in de volgende zin: "Psy doet 100% mee. (100/100=1) naar Psy".
< Honden L | Honden > is de projectie van de algemene toestand van het systeem op de gebonden energietoestand van het voorbeeld van het H2-molecuul en vertegenwoordigt de waarschijnlijkheidsamplitude van het verkrijgen van de gebonden toestand tijdens een waarneming..
Al = < Honden L | Honden > Het kwadraat van de amplitude nemen geeft de waarschijnlijkheid De waarschijnlijkheid van de toestand | Honden L > is: Pl = Al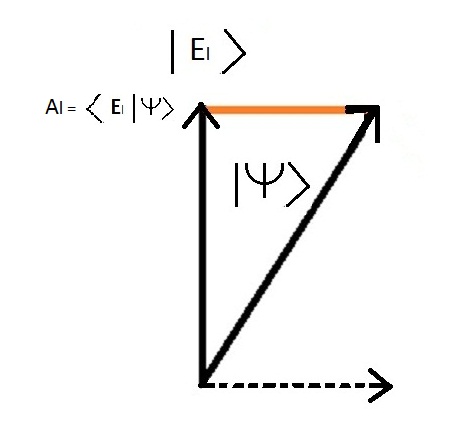² = ( < Honden L | Honden > )² 
De twee waarden < Honden l | Honden > en < Honden nl | Honden > zijn de lengte van de staat | Honden > (die 1) geprojecteerd op de eigen verklaringen | Honden l > en | Honden nl > < Honden l | Honden > is de projectie van de staat | Honden > op de schone staat | Honden l > < Honden nl | Honden > is de projectie van de staat | Honden > op de schone staat | Honden nl >
Dit staat bekend als een equiprobeerbare toestand.
Maar de kenmerken van het systeem kunnen zodanig zijn dat dit niet het geval is, bijvoorbeeld als de bakker dichter bij huis is dan de banketbakker en het erg koud is, is de waarschijnlijkheid van de toestand |bakker> zal sterker zijn dan die van de staat |bakker>.
Dit wordt weergegeven in de onderstaande afbeelding waar Ab groter is dan Ap.
(A is de waarschijnlijkheidsamplitude).
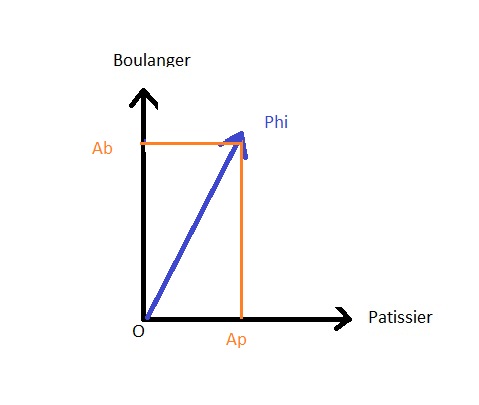De projectie van de staat |Phi> algemeen over de staat |bakker> heeft de waarde Ab die overeenkomt met de waarschijnlijkheidsamplitude van het verkrijgen van deze toestand uit de algemene toestand |Phi> Hetzelfde geldt voor Ap, die de amplitude is van de kans op het verkrijgen van de toestand |bakker>.
Quantum eigenstaten zijn altijd orthogonaal, d.w.z. ze staan loodrecht op elkaar en volgen dus de . Pythagore
voor de rechthoekige driehoek.
Het postulaat zegt dat het kwadraat van de golfamplitude de kans is....
Rekening houden met de algemene toestand van het systeem betekent eenvoudigweg overwegen dat er: de waarschijnlijkheid van de werkelijke toestand van het systeem is dus altijd gelijk aan 1.
Dit is wat het postulaat vermeldt door te zeggen dat de staat |phi> is genormeerd en de norm is volgens afspraak altijd gelijk aan 1 omdat het een kans is.
Wiskundig gezien noteren we < phi | phi > = 1 = | |phi> | ² (de laatste uitdrukking staat voor het kwadraat van de norm van de vector, waarbij de norm van de vector zijn lengte is) Vervolgens wordt deze kans verdeeld in verschillende lagere kansen die overeenkomen met elke eigentoestand, maar met de beperking dat de som van de kwadraten van de amplitudes van de eigentoestanden van het systeem altijd gelijk is aan 1, wat de zekere kans is..
In ons geval hebben we:
Ab² Ap² = 1 De som van de waarschijnlijkheden van alle mogelijke toestanden van het systeem moet gelijk zijn aan 1.
Men kan zeggen dat het bestaan van het systeem over al zijn bestaansmogelijkheden is verspreid, maar zonder enig bestaansverlies, zodat het bestaan behouden blijft.
Als de totale waarschijnlijkheid afneemt, betekent dit immers dat het systeem minder kans heeft om te bestaan en door de waarschijnlijkheid van zijn bestaan tot nul te reduceren, zou het verdwijnen ! De amplitude van de toestand of golffunctie kan positief of negatief zijn, net als de piek of het dal van een golf..
De waarschijnlijkheidsamplitude is dus ofwel negatief ofwel positief, wat we in de afbeelding van de gebonden en ongebonden toestanden van het waterstofmolecuul hebben weergegeven met de symbolen plus en min -. .
(. états molécule hydrogène Pythagoras) Maar de waarschijnlijkheid die het kwadraat is van de amplitude (of het kwadraat van de standaard ) is dus altijd positief, wat normaal is voor een kans.
Wij kunnen ons inderdaad een zekere waarschijnlijkheid voorstellen, dan een minder zekere, dan een onzekere of zelfs een nulwaarschijnlijkheid, maar een negatieve waarschijnlijkheid is zinloos.
Anderzijds kan de waarschijnlijkheidsamplitude negatief zijn.
Stel dan dat we twee gelijke waarschijnlijkheidsamplitudes hebben, maar van tegengestelde tekens die zich naar elkaar voortplanten (het zijn golven).
Als we de kansen bekijken wanneer deze amplitudes zich op dezelfde plaats bevinden, dan heffen de amplitudes van tegengesteld teken op en is hun kwadraat ook nul..
De kans dat je iets waarneemt is nul....
Maar als de amplitudes gescheiden zijn zal hun kwadraat positief zijn (meer door meer is positief maar minder door minder is ook positief) en daarom zal de waarschijnlijkheid om iets waar te nemen niet langer nul zijn....
Wanneer we het over kwantummechanica hebben, denken we aan het probabilistische karakter ervan als een kansspel, maar wat we meestal negeren is dat deze waarschijnlijkheid wordt geschraagd door iets veel verontrustenders, namelijk de amplitude van de waarschijnlijkheidsgolf en die de kwantummechanica haar realiteit geeft.
Het is een evolutieoperator die ervoor heeft gezorgd dat het systeem tijdens een observatie naar de gebonden energietoestand is geëvolueerd.
Dit leidt natuurlijk tot het vijfde postulaat, dat beschrijft hoe het systeem zich tijdens een meting ontwikkelt.
Als we deze operator toepassen op ket | Honden > op een :
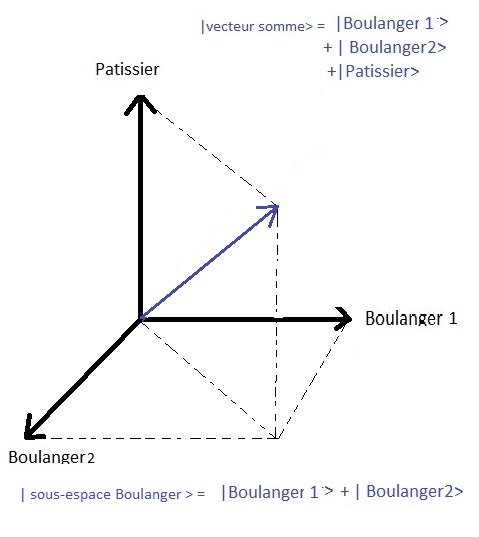
( | Honden L >< Honden L | | Honden nl >< Honden nl | ) | Honden > of | Honden L >< Honden L | Honden > | Honden nl >< Honden nl | Honden > wat resulteert in | Honden L > Al | Honden nl > Anl of zelfs Al | Honden L > Anl | Honden nl > die de ontleding is van de staat | Honden > in de som van zijn eigen energietoestanden | Honden > = Al | Honden L > Anl | Honden nl > De operator heeft de toestand niet veranderd | Honden > maar heeft het gewoon opgedeeld in zijn individuele delen, daarom wordt het de "unit partition operator" genoemd..
Laten we eerst dit begrip "sub-eigenspace" verduidelijken..
Het is slechts een veralgemening van de ontleding van de staat in zijn eigenstaten.
Laten we teruggaan naar het broodvoorbeeld met twee bakkers en een banketbakker.
Indien het onderscheid van het type handel niet waarneembaar is (is geen waarneembare waarde van het systeem)In het geval van een meting is het niet nodig te onderscheiden of het bakker 1 of bakker 2 betreft; het volstaat te weten dat de toestand is geprojecteerd op de eigen deelruimte van de bakker, die in feite, in het onderstaande diagram, overeenkomt met het horizontale vlak dat door de bakkers wordt bevolkt. ! Als er een waarneembaar gegeven zou zijn waarmee we kunnen zien bij welke bakker het brood is gekocht, zou tijdens deze meting de toestand worden geprojecteerd op een van beide bakkers, waardoor de onbepaaldheid van de meting zou worden opgeheven..
Maar als deze eigenschap van het systeem niet wordt waargenomen, blijft het systeem in deze toestand van superpositie van de baker-golffuncties.
Men zegt dat de staat ontaard is.
In de praktijk, wanneer verschillende eigenstaten dezelfde eigenwaarde hebben (dezelfde energie) hebben gezegd dat deze staten ontaard zijn.
Door een extra energiebeperking op het systeem toe te passen die de energie van de ontaarde toestanden verandert zodat er geen gelijkheid meer is, wordt de ontaarding opgeheven..
De kwantumfysica houdt zich hoofdzakelijk bezig met het begrijpen van de structuur van de microscopische wereld, die in wezen bestaat uit resonanties (staande golven) die eigenstaten zijn van de totale energie operator van het systeem (Hamiltonien).
Het vijfde postulaat stelt dat tijdens de meting de toestand van het systeem evolueert naar de toestand waarvan de eigenwaarde is gemeten..
Het is dit zogenaamde postulaat van "golfpakketreductie" of "collaps van de golffunctie" dat de geometrische voorstelling van een vectorprojectie haar fysische realiteit geeft, aangezien het systeem fysisch evolueert in deze operatie..
In dit vijfde postulaat hebben we gezien dat de meting zelf het systeem transformeert.
In het geval van de kwantummechanica bestaat zo'n dynamische vergelijking ook en heet zij de Shroedingervergelijking .
In de mechanica zijn er dus twee mechanismen voor evolutie: de werking van energie in de tijd en de werking van waarneming buiten de tijd.
Deze vergelijking vormt het zesde en laatste postulaat van de kwantummechanica. (zie hieronder).
Het vijfde postulaat betrekt de waarnemer van het systeem bij de evolutie van het systeem.
In de kwantummechanica is de waarnemer dus niet langer onafhankelijk van het fysieke systeem....
De waarnemer en het fysieke systeem vormen een onlosmakelijk geheel....
Men zou kunnen zeggen dat de waarnemer is ingebed in het systeem... (maar niet in de zin van kwantumverstrengeling, die alleen betrekking heeft op de golffunctie).
Wij noemden hierboven het verschijnsel kwantumverstrengeling, dat voortvloeit uit het feit dat een kwantumsysteem dat uit verschillende deeltjes bestaat, wordt beschreven door een enkele golffunctie (eerste aanname) zelfs als de deeltjes zich waarschijnlijk hebben verplaatst in de fysieke ruimte.
Volgens het vijfde postulaat stort de golffunctie tijdens een meting ineen tot een eigen deelruimte, waardoor tegelijkertijd de toestand van alle deeltjes waaruit het systeem bestaat, wordt beïnvloed..
Het was deze implicatie van de kwantummechanica die Einstein officieel nooit kon toegeven, omdat het volgens hem in strijd was met de voortplantingslimiet van elke fysische interactie die door de lichtsnelheid wordt gedefinieerd..
Volgens Einsteins relativiteitstheorie kan geen energie sneller reizen dan de lichtsnelheid....
Licht reist natuurlijk met de lichtsnelheid en dat kan alleen omdat het pure energie is, d.w.z. zonder massa..
Massadeeltjes moeten daarom noodzakelijkerwijs bewegen met een lagere snelheid dan de lichtsnelheid..
De "fysieke" oplossing van deze kwantumparadox werd uitgevoerd door een experiment dat bekend staat als deexpérience_d_Aspect.
Dit experiment bewees onomstotelijk dat de golffunctie niet afhangt van de fysieke ruimte waarin wij leven...: de evolutie ervan tijdens de instorting als gevolg van de observatie vindt plaats op elk punt in de ruimte op hetzelfde moment.
Het experiment van Aspect is vele malen herhaald onder steeds verfijndere omstandigheden om de kwantummechanica tot het uiterste te drijven, maar het heeft nooit toegegeven. ! Van de kwantumtheorie wordt gezegd dat het een niet-lokale theorie is....
De gebruikte termen "niet-lokaliteit" of "niet-scheidbaarheid" zijn gelijkwaardig..
Wij kunnen dus zeggen dat de kwantum-golffunctie de fysieke ruimte overstijgt, zij overstijgt zelfs de ruimte-tijd, aangezien wij sinds Einsteins relativiteitstheorie ruimte en tijd moeten beschouwen als aspecten van dezelfde diepere werkelijkheid. : het ruimte-tijd continuüm.
Een recenter experiment, uitgevoerd in een relativistisch kader en in aansluiting op het experiment van Aspect, heeft de geldigheid van kwantumverstrengeling in een relativistisch kader bevestigd..
( cf Expérience_d_Antoine_Suarez gevonden op de website van de natuurkundige Philippe_Guillemant die een visie biedt waarin de kwantumrealiteit wordt geïntegreerd ) Dit laatste experiment is belangrijk omdat men in een natuurkundig experiment alleen waarden kan meten binnen een bepaald bereik.
In het eerste Aspect-experiment zijn de detectoren voor gecorreleerde fotonen dus (in een enkele kwantumtoestand) waren slechts een paar meter van elkaar verwijderd.
Dit was voldoende om aan te tonen dat kwantumverstrengeling niet het gevolg kon zijn van een onbekend natuurkundig verschijnsel. (verborgen variabele) op sub-lichtsnelheid.
De snelheid van zo'n fenomeen zou noodzakelijkerwijs superluminaal zijn..
Hoewel een dergelijke superluminale snelheid op grond van Einsteins relativiteitstheorie nauwelijks aanvaardbaar is, heeft het eerste experiment van Aspect deze mogelijkheid niet volledig uitgesloten..
Bij het experiment van Antoine Suarez gebeurt dit omdat zelfs de mogelijkheid van een causaliteit tussen de detecties van de twee gecorreleerde fotonen wordt onderdrukt, omdat de relativistische referentieframes waarin de detecties worden gedaan, geen "voor" en "na" toelaten, een essentiële voorwaarde voor causaliteit.: geen enkel foton wordt voor of na het andere gedetecteerd omdat deze detecties niet in hetzelfde tijdsbestek plaatsvinden.
In een relativistische kwantumtheorie kan de golffunctie dus niet langer afhankelijk zijn van de tijd, zoals we hebben gezien in het eerste postulaat.
De reden is dat de tijd wordt teruggebracht tot hetzelfde niveau als de positie, d.w.z. een waarneembare eigenschap van het systeem, en dat de golffunctie onafhankelijk is van de eigenschappen van het systeem. (tweede uitgangspunt).
In zo'n theorie zou de golffunctie | Honden > en niet langer | Psy(t) > .
Tijd zou een waarneembaar T zijn op dezelfde manier als positie P.
De bijzonderheid van dit volledig onrealistische gedachte-experiment zoals gepresenteerd met een "echte kat" is om je te laten nadenken over wat de waarnemer is in de kwantummechanica..
Je hebt in de postulaten over de maatregel (of observatie) dat we niet in detail treden over wat de waarnemer is.
De postulaten zeggen dat er een waarnemer is die de meting doet, maar zeggen verder niets over de aard van de waarnemer. ! In dit experiment wordt een kat geïsoleerd in een doos zodat hij niet kan worden geobserveerd... (gekwantificeerd) op enigerlei wijze.
Dit veronderstelt dat de kat kan worden beschouwd als een kwantumobject, wat in de praktijk niet het geval is, hoewel de kat in theorie a priori kan worden beschouwd als een fysisch systeem, aangezien hij bestaat uit atomen die goed worden beschreven door de kwantummechanica..
In deze kamer bevindt zich ook een flesje met een voor de kat dodelijk gas en een deeltjesdetector die het flesje opent als een deeltje wordt gedetecteerd..
Als een deeltje wordt gedetecteerd is de kat dood, als het niet wordt gedetecteerd is de kat in leven....
Zolang we de gezondheidstoestand van de kat niet "quant ^ hebben waargenomen, blijft hij in een algemene kwantumtoestand die bekend staat als de superpositie van waarneembare eigen toestanden, die zijn | levende kat > en | chat mort > dus we hebben | chat > = | levende kat > | chat mort > Ons kwantumsysteem bestaat uit verschillende componenten: de kat, de detector, het deeltje.
Al deze subsystemen moeten ook in aanmerking worden genomen bij de vaststelling van de golffunctie, dus hebben wij: | deeltje > = | deeltje aanwezig > | afwezig deeltje > en | sensor > = | staatsdeeltje gedetecteerd > | niet-gedetecteerde deeltjestoestand > De wiskunde verbonden aan de kwantummechanica toont aan dat het globale systeem dat we "shroedinger" zullen noemen, is : | shroedinger > = | kat, detector, deeltje > = | chat> ¤ | sensor > ¤ | deeltje > waar ¤ het "tensorproduct" is van de toestandsvectoren....
Aangezien zij zich in dezelfde kwantumtoestand bevinden, wordt gezegd dat deze verschillende subsystemen ingewikkeld zijn..
Dit product gedraagt zich als een gewone producttransactie, het is distributief : A * ( B C ) = A*B A*C In kwantumtermen kunnen we dus de algemene kwantumtoestand ontwikkelen.
Laten we beginnen met het systeem dat alleen bestaat uit de detector en het deeltje.
| detector, deeltje > = | sensor > ¤ | deeltje > = ( | staatsdeeltje gedetecteerd > | niet-gedetecteerde deeltjestoestand > ) ¤ ( | deeltje aanwezig > | afwezig deeltje > ) door het ontwikkelen van :
| detector, deeltje > = | staatsdeeltje gedetecteerd > ¤ | deeltje aanwezig >
| niet-gedetecteerde deeltjestoestand > ¤ | afwezig deeltje >
| niet-gedetecteerde deeltjestoestand > ¤ | deeltje aanwezig >
| staatsdeeltje gedetecteerd > ¤ | afwezig deeltje >
Erwin Shroedinger nweb De eerste twee toestanden zijn gemakkelijk te begrijpen: als het deeltje aanwezig is, is het logisch dat het wordt gedetecteerd, en als het niet aanwezig is, wordt het niet gedetecteerd..
De volgende twee toestanden zijn hoogst onwaarschijnlijk, maar bestaan toch volgens de kwantummechanica, waarvoor alles slechts een waarschijnlijkheidsamplitude is.
Voor de staat | shroedinger > compleet zou het nodig zijn om verder te ontwikkelen met de toestanden van de kat, wat ons zou leiden tot een golffunctie met acht mogelijke eigen toestanden, waarvan er twee zeer waarschijnlijk en zes zeer onwaarschijnlijk zijn..
De twee waarschijnlijke staten zijn:
| chat mort > ¤ | staatsdeeltje gedetecteerd > ¤ | deeltje aanwezig > | levende kat > ¤ | niet-gedetecteerde deeltjestoestand > ¤ | afwezig deeltje > Zolang we het systeem niet hebben waargenomen, wat bijvoorbeeld overeenkomt met het openen van de doos, bevinden we ons in een toestand van superpositie waarin de kat zich in een onbepaalde vitale toestand bevindt..
Hierin ligt de paradox.
Maar we kunnen verder redeneren en dit is wat de natuurkundige deed Eugène_Wigner Nobelprijs voor natuurkunde.
Dit is de théorie_de_l_influence_de_la_conscience Hij meende dat het oog van de waarnemer die de kat dood of levend ziet, ook een kwantumsysteem is met twee toestanden: | oeil > = | oog ziet de dode kat > | oog ziet de kat levend > De toestanden van de volledige golffunctie zouden dan rekening houden met "hallucinerende" toestanden waar het oog dood zou zien, de kat levend....
Maar we kunnen de meetketen blijven beschouwen tot aan de hersenen van de waarnemer, die ook uit atomen bestaan..
Dus de vraag is : wanneer de meting daadwerkelijk wordt uitgevoerd, d.w.z. de ineenstorting van de golffunctie en dus de keuze van het resultaat van het experiment: dode of levende kat.
Wigner zegt dat niets materieels instorting kan veroorzaken omdat alle materie vatbaar is voor beschrijving door de kwantummechanica en dus deel uitmaakt van de golffunctie en men kan ook heel goed de golffunctie van het universum beschouwen.
Als niets materieels de meting verricht, blijft er alleen iets immaterieels over dat dit doet, en dit identificeert Wigner met het bewustzijn, dat uiteindelijk vaststelt wat de waarnemer is.
In zijn interpretatie De waarnemer is het bewustzijn .
Dit brengt ons dichter bij de opvatting van "onafhankelijke werkelijkheid" of "verborgen werkelijkheid" geïntroduceerd door de natuurkundige Bernard_d_Espagnat voor het filosofische begrip van kwantummechanica....
bernard_d_espagnat_physique_quantique_et_réalité_la_réalité_c_est_quoi ;Retrieved from \" https://www.
youtube.
com/watch?v=Jd8FiWJ5v8M; Dit brengt ons ook dichter bij de Vedische opvatting in het oude India van de materiële werkelijkheid, beschreven als ^Maya" of de illusie van de zintuigen..
Deze Maya wordt gemaakt door de oneindige interrelaties tussen drie elementen : richi, chandas en devatta die het subject, het object en hun relatie zijn, kennis (spirituele: van de geest) of de perceptie (materiaal: van het materiaal).
De bewustzijnswaarnemer en de niet-materiële kwantumwerkelijkheid creëren de fenomenologische materiële werkelijkheid.
In dit opzicht is de film Matrix een allegorie van de werkelijkheid, met als enige verschil, en dat is een belangrijk verschil, dat het niet de machines zijn die de illusoire werkelijkheid creëren, maar het bewustzijn zelf.....
Zo kan bewustzijn worden gedefinieerd als de relatie van het subject tot het object door middel van waarneming of kennis.
De volgende drieklanken zijn gelijkwaardig:
samhita_tab_nl
veda filosofie kwantumfysica
rishi onderwerp waarnemer kenner waarnemer
devatta perceptie (subject/object relatie) observatie kennis waarneembaar chandas object waargenomen bekend resultaat van de meting: eigenwaarde van de waarneembare
Dit standpunt zegt dat er tussen twee metingen geen object is en dat het enige object dat bestaat "het waargenomen object" is..
De term klassiek komt overeen met wat de mensheid als geheel op dezelfde manier waarneemt. Maar dit standpunt is in strijd met
kwantumwerkelijkheid, die daarom als volstrekt paradoxaal wordt ervaren.
de basis van de klassieke wereld is de kwantumwereld.
en dat het als zodanig terecht de absolute referentie zou moeten zijn....
zoals het is (Copenhague) en eindelijk de suprematie van zijn positie erkennen....
Het centrale of cruciale probleem tussen de kwantum- en de klassieke werkelijkheid is dat van de decoherentie.
Decoherentie is de overgang van kwantum naar klassiek....
Dat wil zeggen dat wanneer het systeem ontleed is, het klassiek beschrijfbaar is omdat het kwantumaspect verdwenen is..
Bij de bestudering van de kwantummechanica blijkt dat deze op macroscopische schaal tot de wetten van de klassieke mechanica herleidt..
Decoherentie is het feit dat men van de beschrijving van het fysieke systeem door een enkele golffunctie overgaat naar die van een afzonderlijke reeks corpusculen.
Wanneer de golffunctie van een stel deeltjes "decoheres" in de ineenstorting van de meting verdwijnt het golfaspect van de kwantummechanica en blijft alleen het deeltjesaspect over..
De natuurkundige theorie die zich bezighoudt met de beschrijving van een groot aantal lichamen is de statistische thermodynamica, die haar grondslagen heeft in de kwantumtheorie via de Böse-Einstein en Fermi-Dirac kwantumstatistiek.
Deze theorie, die in de 20e eeuw is ontwikkeld, maakt het mogelijk om de resultaten van de 19e-eeuwse macroscopische thermodynamica terug te halen uit microscopische overwegingen..
Thermodynamica werkt in de klassieke wereld van decoherentie, terwijl kwantummechanica werkt in de kwantumwereld van golfcoherentie....
Decoherentie is de overgang van de kwantumwereld naar de klassieke wereld....
Het beheersen van decoherentie is de uitdaging om de kwantumcomputer te produceren.
Alain Aspect in zijn lezing Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_révolution_quantique geeft in dit verband toe (op 1H23mn) dat als de kwantumcomputer op een dag realiteit kan worden, hij geen reden ziet waarom de hersenen dat niet kunnen worden....
Dus de twee niet-fysieke realiteiten: het bewustzijn en de golffunctie zouden eigenlijk één en dezelfde kunnen zijn....
De staat . Phi
van elk niet-relativistisch kwantumsysteem is een oplossing van de tijdsafhankelijke Schrödingervergelijking: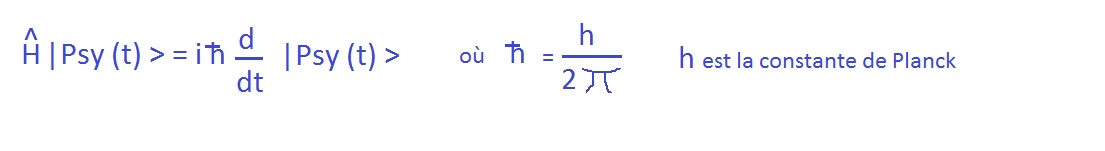 
Het zesde postulaat is het. équation de Schrödinger
.
Dit is de dynamische vergelijking van de kwantummechanica.
Het betekent gewoon dat het de \"totale energie\"-operator van het systeem is, of de Hamiltoniaan, die verantwoordelijk is voor de evolutie van het systeem in de tijd..
(Traditioneel krijgen operatoren in de kwantummechanica een hoedje om ze te onderscheiden van andere wiskundige objecten zoals eigenwaarden.équation de Schrödinger) De vorm van de vergelijking laat zien dat door de Hamiltoniaanse operator toe te passen op de golffunctie van het systeem, we de afgeleide ervan ten opzichte van de tijd verkrijgen, d.w.z. hoe deze in de tijd varieert.
(voor een delta t variatie van tijd dus "dt" hebben we een variatie "d | Psy(t) >" van de golffunctie).
Dus als we de Hamiltoniaanse operator (energie) aan de golffunctie verkrijgen we zijn evolutie in de tijd.
Het is duidelijk dat het energie is die dingen laat gebeuren....
Energie en tijd zijn onlosmakelijk met elkaar verbonden.
Men zegt dat zij een paar geconjugeerde variabelen vormen.
Deze vergelijking is alleen geldig in het niet-relativistische kader.
In het relativistische kader is de geldige vergelijking de Klein-Gordon-vergelijking.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf De Hamiltoniaanse operator H is samengesteld uit alle energieën die op het systeem inwerken.
Deze energieën zijn van tweeërlei aard: kinetische energie en potentiële energie.
Kinetische energie is de energie in een bewegende massa.
Een kiezelsteen die door een raam wordt gegooid, breekt het raam door de kinetische energie die hij bij een bepaalde snelheid heeft gekregen..
Als er verschillende opeenvolgende ruiten zijn, is de snelheid van de steen groter naarmate hij meer ruiten passeert..
De potentiële energie is het gevolg van de krachtvelden die op het systeem van toepassing zijn.
Als een steentje op een ruit op de grond valt, zal het aan snelheid winnen door de gravitationele potentiële energie die het bezit door zijn afstand tot de aarde..
Hoe meer tijd er verstrijkt, hoe meer de potentiële energie wordt omgezet in kinetische energie en wanneer het steentje de grond bereikt, breekt het het raam dankzij de kinetische energie die het heeft verworven ten koste van zijn potentiële energie, die het heeft verloren..
Als je het in een put duwt, zal het hetzelfde proces voortzetten totdat zijn potentiële energie volledig is uitgeput, als dat mogelijk is....
Als we de beweging van een slinger beschouwen (een kiezelsteen die met een touwtje aan een steun is bevestigd) de laatste oscilleert, d.w.z. vanuit de uitgangspositie (onder een bepaalde hoek ten opzichte van de verticaal) wanneer het steentje valt, zal het steentje versnellen tot het touwtje verticaal is, en dan vertragen tot het aan de andere kant stopt in een positie die symmetrisch is met de beginpositie en verticaal is..
De slinger zet zijn potentiële energie om in kinetische energie en vervolgens zijn kinetische energie in potentiële energie, en dit cyclisch.
Als er geen andere kracht op het systeem wordt uitgeoefend, stopt de beweging niet..
In de praktijk zijn er altijd wrijvingskrachten die energie in warmte omzetten totdat deze is uitgeput..
Maar dit laatste geldt alleen in de klassieke mechanica, want in de kwantummechanica is er geen wrijving... ! Een ander systeem waar sprake is van een cyclische transformatie tussen potentiële en kinetische energie is de beweging van een satelliet rond een planeet, bijvoorbeeld de maan en de aarde..
Uit de oplossing van de klassieke mechanica in dit geval blijkt dat de baan van de satelliet een ellips is, d.w.z. er is een moment waarop de maan het verst van de aarde verwijderd is (maximale potentiële energie en minimale kinetische energie, apogeum) en een andere tijd wanneer de maan het dichtst bij de aarde staat... (minimale potentiële energie en maximale kinetische energie, perigeum).
De zojuist beschreven systemen zijn klassieke systemen, maar zij hebben hun correspondentie in het kwantumdomein.
Zo wordt het slingermodel in de kwantummechanica de harmonische oscillator genoemd en komt het satellietmodel overeen met het waterstofatoommodel.: een elektronensatelliet van een proton.
In de kwantummechanica is kinetische energie een operator met massa, en potentiële energie wordt natuurlijk ook voorgesteld door een operator waarvan de vorm afhangt van de betrokken energieën.: elektrische, magnetische potentiaal, ...
De manier waarop massa in de Shroedingervergelijking wordt betrokken, komt uit het eerdere werk van Louis de Broglie die de golf-corpusculaire dualiteit vaststelde: aan elk materiedeeltje kunnen we een golf toekennen waarvan de frequentie evenredig is met de massa.
Dit is gebaseerd op de twee energieformules: E = m c² dat is de energieformule van Einstein's speciale relativiteit : is de massa gelijk aan de energie E = h * nu, de Planck-Einstein relatie die het foto-elektrisch effect verklaart. : is de energie evenredig met de frequentie.
Zo zien we dat in de vergelijking van Shroedinger een resultaat van Einsteins speciale relativiteit is geïntegreerd.
Het is belangrijk te begrijpen dat de betrokken energieën een beperking uitoefenen op het systeem, d.w.z. op de golffunctie.
Bij de behandeling van oscillerende systemen zoals de harmonische oscillator (pendule) of het waterstofatoom (satellieten)Het effect van de energiebeperking is het lokaliseren van de golffunctie in een gebied van de ruimte.
Bijvoorbeeld, een klassiek systeem onderworpen aan geen kracht (een meteoor die verloren gaat in de interstellaire ruimte waar de zwaartekracht van sterren kan worden verwaarloosd.) zal voor onbepaalde tijd in een rechte lijn bewegen.
Het kwantumequivalent is een vlakke golf die zich onbeperkt voortplant, zoals een foton dat aan geen enkele kracht onderhevig is. (fotonen zijn deeltjes zonder enige massa of elektrische lading en zijn daarom niet onderhevig aan enige kracht of energie).
Wanneer de golffunctie een cyclische oplossing heeft (gelokaliseerde golffunctie) de tijd heeft niet langer het effect dat de delen van het systeem zich oneindig van elkaar verwijderen.
Het elektron blijft dicht bij zijn kern, die in het geval van het waterstofatoom het proton is..
Tegelijkertijd, als de kwantumgolf zich cyclisch voortplant in een eindig gebied, overlapt hij zichzelf en interfereert hij dus constructief of destructief met zichzelf..
Bij het oplossen van de Shroedingervergelijking van dergelijke systemen ziet men dat de tijd niet langer ingrijpt in de vorm van de golffunctie en dat alleen de ruimte (de positie) die de vorm van de golf bepaalt.
Dit is het geval bij ondes_stationnaires_nl die al genoemd is.
Dat wil zeggen dat de plaatsen waar interferentie constructief is, altijd dezelfde zijn als de plaatsen waar zij destructief is..
De staande golf is een krachtig concept waarmee we kunnen begrijpen hoe een statisch verschijnsel kan ontstaan uit een dynamisch verschijnsel.
Dit is een van de elementen die de integratie van de kwantumvisie mogelijk maken: alle stabiliteit van de materie die wij ervaren komt voort uit een wirwar van golven die voortdurend in beweging zijn, maar waarvan de interferentieresultaat stabiel is....
Voor het atoom geeft dit goed gedefinieerde banen waarvan de vormen worden geleverd door de oplossingsfuncties van de Shroedingervergelijking, de atoombanen: de wolken zijn de wolken van waarschijnlijkheid van aanwezigheid van het elektron.
Hoe dichter de wolk, hoe groter de kans dat het elektron aanwezig is..
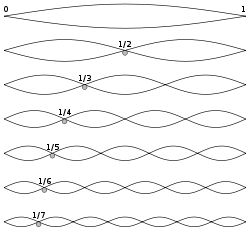
Weergave van de waarschijnlijkheidsamplitude van staande golven (harmonischen) van de harmonische oscillator.
Let op de gelijkenis met de trillingstoestanden (Trillingsknopen en buiken) van een trillende snaar.
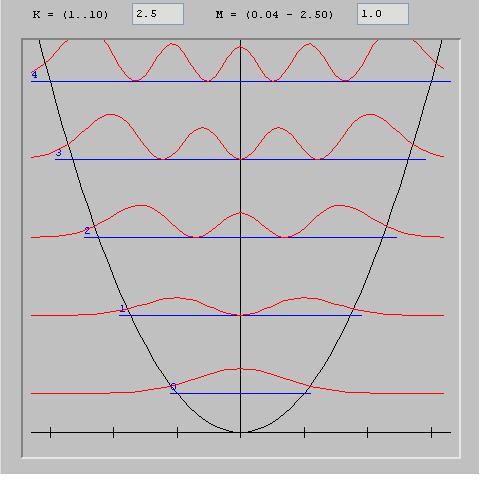
Wij merken op dat in het kwantumgeval (links) de waarschijnlijkheidsamplitude van de golffuncties (in het rood) neemt geleidelijk af naarmate men zich van het centrum verwijdert, d.w.z. in gebieden waar de potentiaal sterker wordt. (parabolische curve in zwart) maar is nooit helemaal nul.
Er is dus een kans dat het deeltje wordt aangetroffen in een afgelegen gebied waar de potentiële energie hoger is dan de kinetische energie, terwijl het klassiek gezien gevangen zou zitten in het gebied waar de potentiële energie lager is dan de kinetische energie..
Dit feit is de reden voor deeffet_tunnel waardoor een kwantumdeeltje een potentiële barrière kan passeren waarvan de energie hoger is dan de energie van het deeltje, omdat de golffunctie aan de andere kant van de barrière niet nul is, waardoor het deeltje daar kan worden waargenomen..
Dit is een gevolg van het niet-lokale aspect van de golffunctie.
Dit is de beperking die de energie oplegt aan de golffunctie om gelokaliseerd te blijven en dus met zichzelf te interfereren om staande golven te produceren die geassocieerd worden met bepaalde waarden van energie. (Gekwantificeerde waarden dus) wat de oorsprong is van het begrip "kwantificatie"..
Tenslotte is het noodzakelijk te spreken over wat aan de oorsprong ligt van de kwantumtheorie: de constante_de_Planck die voorkomt in de Shroedingervergelijking.
Deze constante werd geïntroduceerd door de natuurkundige Max_Planck de waarde van de warmtestraling van de materie als functie van de temperatuur verklaren.
De waargenomen wet die deze straling volgt, dwingt ons te bedenken dat thermische energie niet continu wordt uitgezonden, maar in pakketjes of "quanta"..
Dit is het eerste bewijs van het kwantumkarakter van materie....
In de natuurkunde wordt actie gedefinieerd als het product van energie en tijd....
Het is vrij intuïtief: wanneer een energie gedurende een bepaalde tijd werkt, genereert zij een bepaalde actie waarvan de waarde evenredig is met die van de energie en met de tijdsduur waarin zij werkt.
De constante van Planck vertegenwoordigt de kleinst mogelijke actie in de fysieke wereld....
Het is een universele constante van de fysica die de kwantumnatuur van de werkelijkheid kenmerkt....
De waarde van deze constante is extreem klein: 6,62607004 × 10-34 m2 kg / s maar het is niettemin niet nul.
die Planck-eenheden worden genoemd.
De fysieke wereld zoals beschreven door de kwantummechanica heeft dus een grens in het oneindig kleine, waarboven we niet meer in termen van natuurkunde kunnen spreken, het is tenslotte een rand van de fysieke wereld.
Als er een rand is, een limiet, dan is dat een natuurlijke kwantumbeperking voor de golffunctie en dus voor de kwantisering (die op zichzelf, zoals we hebben gezien, een kracht is...).
De constante van Planck bepaalt de pixelvorming van het heelal.
De meest fundamentele oorsprong van kwantificering is ook te vinden in de werking van het bewustzijn, dat van nature niet continu is.
Immers, als we de waarneming door een subject van een object dat een gezichtspunt in het bewustzijn is, beschouwen, is dit alleen mogelijk door onderscheid van het bewustzijn van verschillende mogelijke gezichtspunten.
Om ze te kunnen identificeren, moeten de gezichtspunten gescheiden zijn, anders zouden alle gezichtspunten samensmelten en zou er geen echte observatie zijn..
Discriminatie is de eigenschap van het intellect die in die zin een fundamentele eigenschap van het bewustzijn is.
Wij vinden dus de elementen die aanwezig zijn in de kwantumpostulaten van meting.
"
1.5.1.Analyse van het aforisme
gedicht kwantumaanpassing link naar de postulaten
Wat is de golffunctie of toestandsvector of "ket" (van beugel , haak in het Frans) . Premier postulat
mogelijk de probabilistische structuur van de golffunctie, de verschillende mogelijke eigenstaten van de ket . Troisième postulat is volbracht de dynamiek van de Hamiltoniaanse operator totale energie van het systeem dat verantwoordelijk is voor de evolutie. . Deuxième postulat onder het oog van het geweten de postulaten van de meting, d.w.z. de noodzakelijke tussenkomst van de waarnemer . Quatrième postulat alleen wat mogelijk is wordt bereikt alleen de eigenwaarden van de observabele kunnen worden verkregen en de toestand van het systeem is dan de overeenkomstige eigen toestand. . Cinquième postulat Wat mogelijk is wordt bereikt de Schrödingervergelijking, de kwantumdynamische vergelijking.... . Sixième postulat
De grote moeite die wetenschappers hebben om de boodschap van de kwantumtheorie te aanvaarden, verklaart waarom zo weinig mensen er toegang toe hebben..
Hier vindt u een samenvatting van deze situatie, geanalyseerd door Jean Staune en gerapporteerd door Bruno Lussato: bruno_lussato_les_plus_grandes_désinformations_de_l_histoire_des_sciences
(blog waar ik in 2009 een verslag achterliet van de conferentie die Alain Aspect in 1982 in Toulouse gaf toen hij de Franse universiteiten bezocht om de resultaten van zijn werk te presenteren.bruno lussato de grootste misinformatie in de geschiedenis van de wetenschap nweb) Deze tekst had geschreven kunnen worden en waarschijnlijk veel beter door een groot aantal deskundige mensen die deel uitmaken van het wetenschappelijke "establishment", maar hun onwil om dat te doen heeft er enerzijds toe geleid dat ik de domeinnaam quantum heb kunnen reserveren.
org die vreemd genoeg beschikbaar was en anderzijds om tientallen uren te besteden aan het uitwerken van deze tekst die waarschijnlijk nog moet worden verbeterd...
van alle ruimte-tijd omstandigheden, d.w.z. van alle
alle fysieke omstandigheden.
omdat het alle informatie over het fysieke systeem bevat op een manier die
niet-lokaal.