Os postulados da mecûÂnica quûÂntica
versûôÈo disponûôÙvel em : en it ru zh es ja de nl fr
data de criação : 20240129- data de actualiza&occedil&atlideo: 20221007- data de gera&ccdelão : 20241110_231431
Este artigo apresenta em detalhe o postulats_de_la_mûˋcanique_quantique de consideraûÏûçes matemûÀticas e geomûˋtricas simples e analogias retiradas da vida quotidiana.
Na fûÙsica, conceitos relacionados com objectos matemûÀticos sûÈo desenvolvidos para estabelecer teorias que permitem que o mundo fûÙsico seja representado atravûˋs das suas leis de funcionamento.
A mecûÂnica clûÀssica ou teoria de Newton ûˋ a teoria que nos permite representar o funcionamento da matûˋria em escalas sensûÙveis û percepûÏûÈo humana e a que chamamos macroscû°pica.
Em escalas cosmolû°gicas, esta teoria ûˋ generalizada atravûˋs das teorias relativistas de Einstein.
A relatividade geral ûˋ a teoria que mais se ocupa da forûÏa da gravidade.
A mecûÂnica quûÂntica ûˋ a teoria que nos permite representar o funcionamento da matûˋria a nûÙvel microscû°pico, embora a fronteira entre o microscû°pio e o macroscû°pico nûÈo esteja claramente definida em termos de escala, de modo que podemos ter um comportamento quûÂntico a escalas macroscû°picas, como na laser ou o cables_ûˋlectriques_supraconducteurs A teoria quûÂntica nûÈo trata de uma forûÏa particular da natureza como a relatividade geral, ûˋ mais uma linguagem.
A linguagem dos objectos quûÂnticos.
Assim, podemos aplicar esta linguagem a vûÀrias forûÏas ou sistemas, quantificando-os assim.
O conjunto de conceitos quûÂnticos gira em torno de seis postulados bûÀsicos que definem totalmente a teoria quûÂntica.nweb cabos supercondutores de energia Apresentaremos estes seis postulados e tentaremos identificar o seu significado de uma forma simples.
A expressûÈo do primeiro postulado como definido no livro de Cohen-Tanoudji " MecûÂnica QuûÂntica Volume 1" ûˋ :
Num tempo t fixo, o estado de um sistema fûÙsico ûˋ definido pelos dados
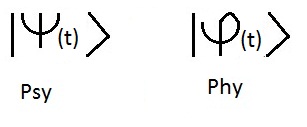
de um ket ou funûÏûÈo de onda ou vector de estado anotado |psy(t)> pertencentes ao espaûÏo estatal".
Postulado I nweb
A letra grega Psy ûˋ usada para designar a funûÏûÈo de onda, usamos
tambûˋm indiferentemente a letra Phy.

O primeiro conceito de mecûÂnica diz respeito û representaûÏûÈo do estado do sistema fûÙsico.
Esta ûˋ uma forma natural de definir o tema do estudo. Aqui dizemos simplesmente que o sistema existe
e que o seu estado pode ser representado por uma funûÏûÈo dependente do tempo
isto porque o estado do sistema nûÈo ûˋ, a priori, estûÀtico mas dinûÂmico.
Na mecûÂnica clûÀssica o sistema fûÙsico ûˋ representado pelo ponto "material ".
Um sistema complexo serûÀ representado por um conjunto de pontos de material ligado
entre eles para formar um objecto sû°lido ou nûÈo sû°lido (ligaûÏûçes rûÙgidas ou nûÈo rûÙgidas, por exemplo: cristal ou gûÀs).
O primeiro postulado afirma simplesmente que o estado do sistema num determinado momento ûˋ û¤nico
e pertence a um conjunto de possûÙveis estados agrupados num conjunto
matemûÀtica chamada "espaûÏo estatal"^.
Falamos de espaûÏo e nûÈo simplesmente de um conjunto porque o estado quûÂntico ûˋ um vector
que ûˋ um objecto matemûÀtico que representa uma direcûÏûÈo num espaûÏo.
Todos nû°s conhecemos o espaûÏo tridimensional (comprimento, largura, altura ou profundidade, dependendo da orientaûÏûÈo das duas primeiras dimensûçes)
û o espaûÏo fûÙsico em que vivemos.
O espaûÏo dos estados em que os sistemas quûÂnticos " vivos" nûÈo ûˋ um espaûÏo fûÙsico, ûˋ um espaûÏo abstracto (EspaûÏo Hilbert)
e a sua dimensûÈo ûˋ infinita para representar a infinidade de estados possûÙveis que existem mesmo para sistemas fûÙsicos simples.
Vamos fazer uma analogia com um exemplo da vida quotidiana
para compreender como um sistema quûÂntico ûˋ modelado.
Imagine uma pessoa sentada em silûˆncio no seu apartamento e de repente
apercebe-se de que tem de sair para comprar pûÈo.
Ela prepara-se para partir e na sua mente continua a hesitar sobre o lugar onde ela vai para comprar pûÈo.
Ela pode escolher entre uma padaria mais acima na rua ou uma pastelaria que tambûˋm faz
que estûÀ mais abaixo na rua.
Descendo as escadas para sair, pode-se dizer que hûÀ dois estados possûÙvel na sua mente que correspondem û s duas opûÏûçes de comprar pûÈo. Estas opûÏûçes podem ser notadas de forma quûÂntica:
estado 1: |padeiro>
estado 2: |pastelaria>
O estado de espûÙrito da pessoa ûˋ uma combinaûÏûÈo destas duas possibilidades:
| Estado> = |padeiro> + |pastelaria>
Os dois estados sûÈo completamente incompatûÙveis: ou ela compra o pûÈo no padeiro, ou na confeitaria. Ambas as possibilidades tûˆm nada em comum, eles nûÈo partilham nada. Geometricamente dir-se-ûÀ que sûÈo ortogonais (perpendicular) e representaûÏûÈo geomûˋtrica no espaûÏo (dos estados assim) serûÀ:
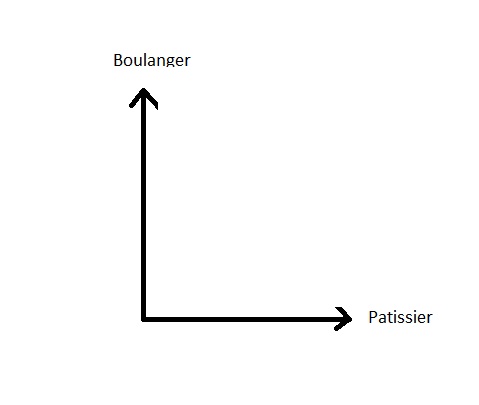
Temos, portanto, duas direcûÏûçes muito distintas que nada tûˆm em comum.
Se a seta (vector) padeiro estava inclinado para a seta (vector) pastelaria
entûÈo isto significaria que ir comprar de
o padeiro estûÀ um pouco ligado a ir comprar
na pastelaria, o que nûÈo ûˋ o caso, sûÈo dois
opûÏûçes incompatibilidades: ortogonal, ou seja, em ûÂngulos rectos: nûÈo partilham nada em termos de lideranûÏa.
Por outro lado, o estado do sistema, ou seja, o estado de espûÙrito
da pessoa ûˋ uma chamada combinaûÏûÈo linear dos dois estados.
Dizemos que temos uma mistura de estados. O verdadeiro estado misto nûÈo
nûÈo corresponde a nada observûÀvel: nûÈo sabemos
nûÈo onde o pûÈo ûˋ comprado.
Esta combinaûÏûÈo linear das duas possibilidades corresponde a
û soma dos dois vectores que representam os estados observûÀveis.
A soma de dois vectores ûˋ realizada da seguinte forma : fazemos
A partir do fim do primeiro vector e do segundo vector
soma resultante do inûÙcio do primeiro e que termina no final
do segundo.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
Dizia-se que o espaûÏo de estado era um espaûÏo vectorial, ou seja, um espaûÏo de direcûÏûçes, isto implica que na representaûÏûÈo geomûˋtrica podemos mover os vectores sem os alterar natureza, continuam a ser os mesmos vectores: apontam na mesma direcûÏûÈo. Tambûˋm para simplificar a representaûÏûÈo, todos os vectores sûÈo feitos para comeûÏar do mesmo ponto para indicar que apenas as direcûÏûçes existem neste espaûÏo. Isto ûˋ chamado um espaûÏo vectorial em oposiûÏûÈo a a um espaûÏo de pontos que em matemûÀtica ûˋ chamado de espaûÏo afim. ( O ecrûÈ em que estûÀ a ler este texto ûˋ um exemplo de espaûÏo afim onde os pixels representam pontos nesse espaûÏo.estado soma vector img)
A representaûÏûÈo geomûˋtrica ûˋ obviamente feita num espaûÏo de pontos porque um espaûÏo vectorial
ûˋ uma abstracûÏûÈo pura e sû° pode ser representada no espaûÏo que percebemos com pontos (posiûÏûçes) diferente.
Mas isto nûÈo existe no espaûÏo de estado onde todas as representaûÏûçes de um vector em diferentes
as posiûÏûçes no espaûÏo de representaûÏûÈo correspondem a um û¤nico vector no espaûÏo vectorial.
Assim, o Estado pode ser representado da seguinte forma :
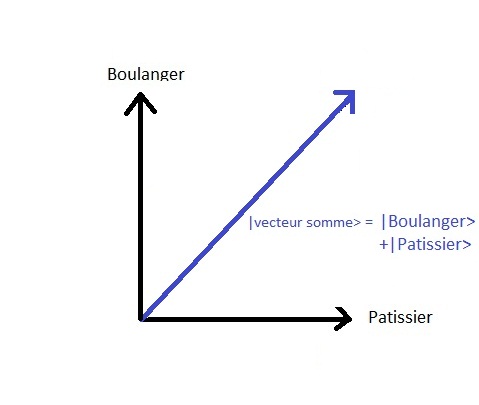
Aqui a dimensûÈo do espaûÏo de estado ûˋ duas. Se existisse uma terceira opûÏûÈo
com outro padeiro numa rua adjacente | padeiro2 > entûÈo o espaûÏo de estado seria de dimensûÈo trûˆs, etc..
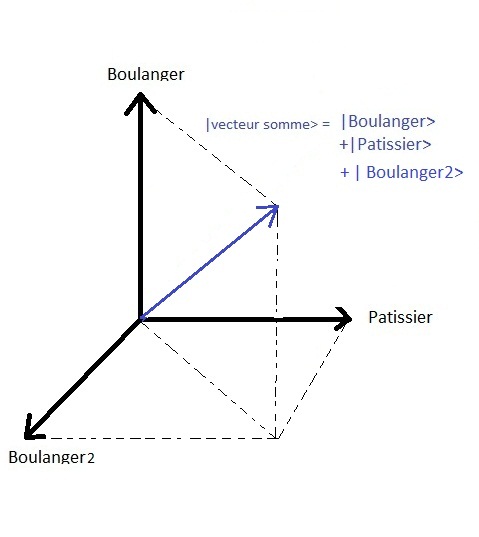
Em fûÙsica, os sistemas de dois estados podem ser modelados da mesma forma.
Este ûˋ o caso da molûˋcula de hidrogûˋnio ionizado. A molûˋcula de hidrogûˋnio
ûˋ composto por dois nû¤cleos de hidrogûˋnio, ou seja, dois prû°tons
e o facto de ser ionizado significa que um electrûÈo foi removido do mesmo
dos dois que possui naturalmente. Por exemplo
porque ûˋ simples : " a um û¤nico electrûÈo"^.
Os dois estados posicionais possûÙveis para o electrûÈo sûÈo :
A representaûÏûÈo geomûˋtrica ûˋ:
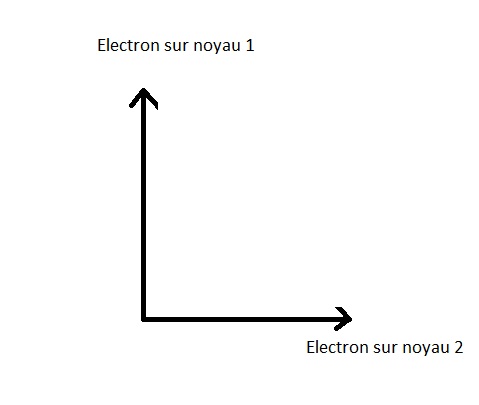
û evidente que o electrûÈo nûÈo pode ser encontrado (ou melhor, a ser encontrado, ou seja : ser observado) ao mesmo tempo no nû¤cleo 1 e no nû¤cleo 2, estes estados sûÈo ortogonais.
Na expressûÈo do postulado, sûÈo utilizados sinû°nimos para designar o vector de estado, que ûˋ chamado indiferentemente
vector de estado, funûÏûÈo de onda ou ket. Estes diferentes nomes correspondem a diferentes aspectos matemûÀticos do vector estatal.
Veremos o aspecto da funûÏûÈo de onda na explicaûÏûÈo do segundo postulado e o aspecto "ket" no terceiro.
Em resumo, o estado quûÂntico ûˋ representado pelo vector dado (direcûÏûÈo) num espaûÏo vectorial (de direcûÏûçes),
este vector ûˋ chamado de " vector de estado"^.
Na mecûÂnica clûÀssica, o estado ûˋ representado pelo "ponto material" que ûˋ definido pelas suas propriedades fûÙsicas posiûÏûÈo e velocidade.
û importante notar que na mecûÂnica quûÂntica o estado do sistema ûˋ totalmente independente do estado do sistema.
as propriedades fûÙsicas do sistema. O estado ûˋ definido de forma abstracta e poder-se-ia dizer "nûÈo fûÙsica".
Isto serûÀ detalhado na apresentaûÏûÈo dos seguintes postulados atravûˋs da noûÏûÈo de "base de representaûÏûÈo vectorial do estado"^.
Mas pode notar-se que o primeiro postulado faz depender o vector de estado apenas do tempo e nûÈo da posiûÏûÈo
que ûˋ o espaûÏo. Isto significa que a funûÏûÈo de onda ûˋ nûÈo-local.
Obviamente a relatividade ensina-nos que o tempo e o espaûÏo formam um continuum e, portanto, se uma formulaûÏûÈo de
a mecûÂnica quûÂntica tem em conta pelo menos a relatividade especial, o vector de estado nûÈo depende de
do tempo. Esta teoria ûˋ a electrodinûÂmica quûÂntica ou teoria quûÂntica do campo electromagnûˋtico.
Sendo a relatividade especial muito ligada ao electromagnetismo pelo facto de Einstein ter produzido esta teoria
para remover os paradoxos que a teoria eletromagnûˋtica de Maxwell levantou.
Os conceitos quûÂnticos nûÈo foram concebidos por pura imaginaûÏûÈo. Pelo contrûÀrio, eles foram forjados no fogo da experimentaûÏûÈo
de microfûÙsica que exigia que estes conceitos estivessem devidamente representados.
Embora totalmente abstracto, o estado quûÂntico ûˋ, no entanto, real.
û esta realidade do estado quûÂntico que frequentemente continua a ser a coisa mais difûÙcil de admitir, mesmo que seja inevitûÀvel.
O funcionamento da matûˋria, que ûˋ a coisa mais concreta, ûˋ governado por algo totalmente abstracto.
No entanto, ûˋ impossûÙvel contornar esta dificuldade, uma vez que este conceito quûÂntico ûˋ extraordinariamente sû°lido.
A situaûÏûÈo cognitiva ûˋ algo semelhante û descoberta de ondas electromagnûˋticas. Estas ondas foram, teoricamente, as primeiras
descoberto atravûˋs da combinaûÏûÈo das equaûÏûçes de Maxwell descrevendo campos elûˋctricos e magnûˋticos.
A sua combinaûÏûÈo forneceu uma equaûÏûÈo de propagaûÏûÈo de onda com uma velocidade constante. Era uma noûÏûÈo abstracta
e novas, mas as experiûˆncias demonstraram que os campos elûˋctricos e magnûˋticos produzem efectivamente ondas
que podiam ser controladas e utilizadas, o que levou û comunicaûÏûÈo via rûÀdio.
Vimos que esta velocidade ûˋ a velocidade medida da luz.
Da mesma forma, o conceito muito abstracto de uma funûÏûÈo de onda tornou-se muito concreto emintrication_quantique e deu origem û ûÀrea tecnolû°gica de cryptographie_quantique
Postulat_II
"Uma quantidade fûÙsica observûÀvel 'a' ûˋ descrita por um operador 'A' que actua no espaûÏo de estado; este operador ûˋ um observûÀvel.
" Na mecûÂnica clûÀssica, vimos que sûÈo as propriedades do ponto material, a sua velocidade e a sua posiûÏûÈo que determinam o seu estado.
Por exemplo, a velocidade e a posiûÏûÈo de uma bola num campo de tûˋnis ou de um planeta no sistema solar.
A posiûÏûÈo e velocidade de um objecto macroscû°pico sûÈo determinadas a cada instante e isto define completamente o estado do sistema.
A evoluûÏûÈo da bola de tûˋnis no espaûÏo define em cada momento o estado do jogo, se a bola estûÀ em movimento, "out" ou nûÈo ou imû°vel no chûÈo depois de ter apanhado a rede.
E ûˋ a histû°ria dos seus estados que define o jogo e o seu resultado.
Por outro lado, na mecûÂnica quûÂntica, o estado geral de um sistema reduzido a uma partûÙcula como o electrûÈo no exemplo anterior jûÀ nûÈo estûÀ associado a uma posiûÏûÈo ou velocidade particular, mas a uma mistura de todas as posiûÏûçes ou velocidades possûÙveis.
Alûˋm disso, nûÈo podemos observar todas as propriedades do sistema ao mesmo tempo que na mecûÂnica clûÀssica.
Se o sistema estûÀ num estado posicional, nûÈo estûÀ num estado energûˋtico e vice versa.
No exemplo do pûÈo temos estados posicionais que sûÈo o padeiro e o pasteleiro que indicam o local onde o pûÈo ûˋ comprado mas, como veremos, estes nûÈo sûÈo estados energûˋticos.
Tal como no exemplo da molûˋcula de hidrogûˋnio, o facto de o electrûÈo estar localizado no nû¤cleo 1 ou nû¤cleo 2 representa estados posicionais, mas nûÈo sûÈo em si estados energûˋticos da molûˋcula.
Num sistema quûÂntico, as diferentes propriedades partilham o mesmo espaûÏo de estados mas os estados correspondentes a diferentes propriedades nûÈo sûÈo necessariamente representados pelas mesmas direcûÏûçes no espaûÏo.
Isto significa que se o espaûÏo ûˋ bidimensional entûÈo haverûÀ dois possûÙveis estados posicionais mas tambûˋm dois possûÙveis estados energûˋticos e que os estados energûˋticos nûÈo tûˆm as mesmas direcûÏûçes que os estados posicionais.
No caso da molûˋcula de hidrogûˋnio (ionizado) os possûÙveis estados energûˋticos sûÈo:
| Estado:ûˋnergie> = |estado relacionado> |estado sem restriûÏûçes>
na representaûÏûÈo "dinûÂmica ou energûˋtica" da molûˋcula de hidrogûˋnio.
O estado geral do sistema ûˋ completamente independente das suas propriedades, por isso para o pûÈo podemos escrever:
| Estado> = |determinaûÏûÈo> |renû¤ncia> = |padeiro> |padeiro>
Para a molûˋcula de hidrogûˋnio que chama El (estado relacionado) e Enl (estado sem restriûÏûçes) os estados energûˋticos e P1 e P2 os estados de posiûÏûÈo, temos:
| Estado> = | O > | Enl > = | P1 > | P2 >
O facto de o Estado ser independente das suas propriedades observûÀveis e poder ser expresso independentemente delas ûˋ uma caracterûÙstica fundamental da mecûÂnica quûÂntica.
As propriedades sûÈo representadas por operadores matemûÀticos que, quando aplicadas ao estado quûÂntico, determinam os possûÙveis estados para essa propriedade.
Um operador em matemûÀtica ûˋ o que faz um valor evoluir no sentido lato.
Por exemplo, para adiûÏûÈo o operador "3 " aplicado a "2" dûÀ "3 2"^=Mudamos o valor de "^2" para "5"^ aplicando o operador "^3 "^ (adiûÏûÈo do valor trûˆs) Na mecûÂnica quûÂntica, o operador faz o estado evoluir.
O postulado diz que o operador " actua" sobre o espaûÏo de estado.
Deixe P ser o operador de posiûÏûÈo e E o operador de Energia (na realidade, o operador energûˋtico ûˋ designado por H para hamiltonien_pt que ûˋ a funûÏûÈo energûˋtica total definida em mecûÂnica geral por Hamilton como a soma de todas as energias que actuam no sistema).
De acordo com o segundo postulado, estes operadores representam as propriedades correspondentes (posiûÏûÈo e energia) do sistema.
Ao aplicar (fazer funcionar) o operador de posiûÏûÈo sobre o estado da molûˋcula de hidrogûˋnio que temos:
P | estatuto > = | P1 > ou P | estatuto > = | P2 >.
Aplicar o operador no Estado significa observar o bem correspondente ao operador, aqui a posiûÏûÈo.
Da mesma forma com o operador de energia.
H | estatuto > = | O > ou H | estatuto > = | Enl >.
Podemos ver que quando aplicamos um operador a um estado, fazemos este estado evoluir para um estado pertencente a este operador em particular, chamamos a este estado " estado de limpeza"^ do operador.
O resultado pode ser qualquer estado possûÙvel para o sistema e para o operador (a propriedade medida).
O Estado " molûˋcula de ligaûÏûÈo" ûˋ um estado de origem do operador energûˋtico enquanto o "electron sobre o nû¤cleo 1" ûˋ um eigenstate da posiûÏûÈo do operador.
Para a molûˋcula de hidrogûˋnio no estado ligado, o electrûÈo encontra-se numa posiûÏûÈo indeterminada entre os dois nû¤cleos de hidrogûˋnio.
Pode-se dizer que o eigenstate energûˋtico ûˋ uma combinaûÏûÈo linear de estados posicionais, que podem ser representados como:
| O > = | P1 > | P2 >
Pode-se dizer que os dois estados posicionais se somam a um estado energûˋtico: quando o electrûÈo ûˋ partilhado pelos dois nû¤cleos, a molûˋcula ûˋ ligada, diz-se que os dois estados posicionais interferem construtivamente para formar o estado " de energia.
da mesma forma que o estado nûÈo vinculado serûÀ representado por | Enl > = | P1 >- | P2 >
diz-se que os dois estados posicionais interferem destrutivamente para criar o estado de energia "unbound"^.
Se retomarmos a analogia do pûÈo, o estado de espûÙrito da pessoa ûˋ uma hesitaûÏûÈo entre ir comprar pûÈo ao padeiro ou ao pasteleiro, mas tambûˋm entre ir comprar pûÈo ou nûÈo comprar pûÈo.
Pode dizer-se que a determinaûÏûÈo de sair e comprar pûÈo ûˋ uma interfûˋrence_pt de todas as possibilidades de ir e comprar pûÈo, enquanto a renû¤ncia ûˋ uma interfûˋrence_pt destrutivas destes mesmos estados possûÙveis.
Consideramos todas as possibilidades que podem acontecer ao sistema e que estûÈo todas incluûÙdas no espaûÏo estatal.
Geometricamente, isto pode ser representado da seguinte forma:
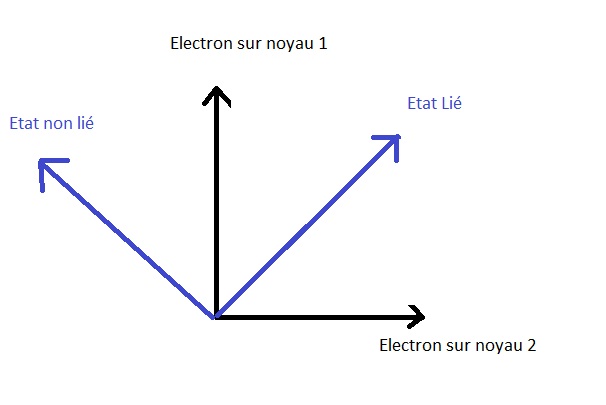
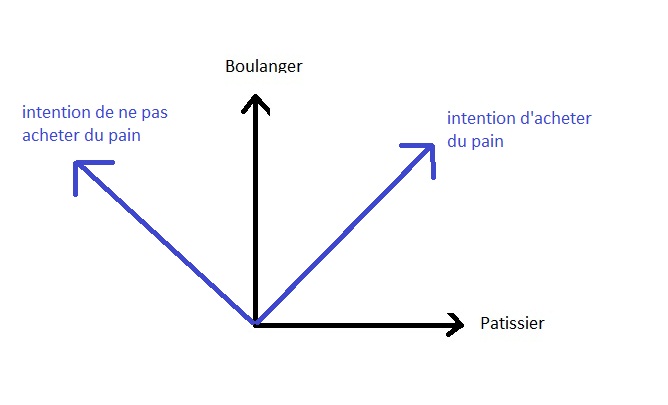 Pode-se ver que a energia observûÀvel declara (estados vinculados ou nûÈo vinculados da molûˋcula) sûÈo tambûˋm ortogonais porque correspondem a possûÙveis opûÏûçes energûˋticas que sûÈo incompatûÙveis entre si.
Pode-se ver que a energia observûÀvel declara (estados vinculados ou nûÈo vinculados da molûˋcula) sûÈo tambûˋm ortogonais porque correspondem a possûÙveis opûÏûçes energûˋticas que sûÈo incompatûÙveis entre si.
O estado do sistema (vector de estado) ûˋ ela prû°pria independente da sua representaûÏûÈo no espaûÏo estatal, quer em relaûÏûÈo û energia, quer em relaûÏûÈo û posiûÏûÈo.
Diz-se que os egocentrismos associados a um operador sûÈo uma base para representar o vector estatal (aqui base azul ou preta) Assim, para o vector estatal, temos uma base de representaûÏûÈo para o operador de posiûÏûÈo e uma base de representaûÏûÈo diferente para o operador de energia.
1.1.2.PrincûÙpio d incertitude de Heisenberg
O principe_d_incertitude_de_Heisenberg segue directamente os postulados da mecûÂnica quûÂntica.
Vimos que, em geral, os estados prû°prios de dois observûÀveis nûÈo sûÈo representados pelos mesmos vectores e que um estado energûˋtico, por exemplo, serûÀ representado por uma combinaûÏûÈo linear (sobreposiûÏûÈo) de estados posicionais.
Neste caso, ûˋ evidente que ûˋ impossûÙvel observar tanto a propriedade de posiûÏûÈo como a propriedade energûˋtica de um sistema durante a mesma mediûÏûÈo, uma vez que os seus egocentrismos sûÈo incompatûÙveis.
Matematicamente, dizemos que os operadores nûÈo mudam.
Isto significa que se os dois operadores forem sucessivamente aplicados ao sistema numa ordem diferente, entûÈo o estado final serûÀ diferente.
Na prûÀtica, numa experiûˆncia quûÂntica, observa-se um grande nû¤mero de partûÙculas que dûÀ um resultado estatûÙstico global em que parece que quanto mais preciso ûˋ o valor energûˋtico, menos precisa ûˋ a posiûÏûÈo e vice-versa.
1.1.3.RepresentaûÏûÈo da funûÏûÈo de onda no espaûÏo fûÙsico
A diferenûÏa entre o vector de estado e a funûÏûÈo de onda ûˋ que o vector de estado ûˋ independente do espaûÏo fûÙsico, enquanto que a funûÏûÈo de onda nûÈo o ûˋ, porque se propaga no espaûÏo fûÙsico.
Na mecûÂnica quûÂntica, diz-se que a funûÏûÈo da onda ûˋ uma projecûÏûÈo do vector de estado no espaûÏo fûÙsico.
Na imagem abaixo, representamos o aspecto ondulatû°rio (funûÏûÈo de onda) de estados quûÂnticos
para visualizar como a onda interfere destrutivamente ou construtivamente por adiûÏûÈo ou subtracûÏûÈo.
O funcionamento fundamental de uma onda ûˋ o mesmo quer se trate de uma onda quûÂntica, uma
electromagnûˋtica ou, por exemplo, uma onda na superfûÙcie de um corpo de ûÀgua (vagueletas).
Uma onda tem sempre um canal e um pico de oscilaûÏûÈo (da onda) em torno de um valor mûˋdio (a superfûÙcie plana da ûÀgua).
Os prû°s somam-se (assim como os menos) e os prû°s e os contras subtraem e anulam-se mutuamente.
Por exemplo, se um canal de ondas se encontrar com o pico de outra onda, os dois cancelam-se um ao outro, deixando
a superfûÙcie plana da ûÀgua no ponto de sobreposiûÏûÈo.
1.1.3.1.Estados da molûˋcula de hidrogûˋnio
Os estados de onda de um ûÀtomo ou molûˋcula correspondem a ondes_stationnaires_pt
que sûÈo ondas que nûÈo se propagam mas permanecem principalmente localizadas numa regiûÈo limitada
do espaûÏo, aqui em torno dos nû¤cleos de hidrogûˋnio.

O segundo postulado introduz, portanto, os operadores que sûÈo aplicados aos estados para os transformar.
Podemos portanto dizer que o vector de estado representa o aspecto estûÀtico da realidade quûÂntica, enquanto o operador representa o aspecto dinûÂmico desta mesma realidade.
O terceiro, quarto e quinto postulados descrevem o prû°prio processo de observaûÏûÈo de um sistema quûÂntico.
Postulat_III
Medida : valores possûÙveis de uma quantidade fûÙsica A observûÀvel "A mediûÏûÈo de uma quantidade fûÙsica A sû° pode dar um valor prû°prio da quantidade A observûÀvel correspondente entre todas as possûÙveis.
" Temos visto que os estados observûÀveis de uma propriedade de um sistema quûÂntico sûÈo chamados "eigenstates" (deste observûÀvel).
Cada "eigenstate" tem associado um ^valor prû°prio" que ûˋ o resultado da mediûÏûÈo.
Por exemplo, para a molûˋcula de hidrogûˋnio serûÀ o nûÙvel de energia da molûˋcula que ûˋ diferente se a molûˋcula estiver no seu estado ligado ou nûÈo ligado.
Na analogia do pûÈo, pode-se imaginar que o resultado ûˋ a mudanûÏa na quantidade de dinheiro na bolsa que diminuiu quando o pûÈo foi comprado.
O valor prû°prio ûˋ um nû¤mero enquanto o eigenstate ûˋ, como jûÀ vimos, um vector.
Atûˋ agora sû° utilizûÀmos a direcûÏûÈo do vector, que tambûˋm estûÀ associada a uma dimensûÈo do espaûÏo de estado, uma vez que esta ûˋ a noûÏûÈo mais importante relativa ao estado quûÂntico.
Em matemûÀtica, o valor natural associado a um vector ûˋ o seu comprimento.
Este comprimento ûˋ abstracto (nûÈo ûˋ espaûÏo fûÙsico por isso nûÈo ûˋ medido em metros).
Por esta razûÈo, foi criado um termo mais geral que se refere a comprimento ou escala, daûÙ o nome " valor escalar"^..
O escalar ûˋ, portanto, o valor numûˋrico associado ao comprimento de um vector.
Se multiplicarmos o comprimento de um vector por um nû¤mero, obteremos um vector cujo comprimento ûˋ um mû¤ltiplo do valor inicial, serûÀ numa escala diferente, o seu novo valor "scalar"^.
Aqui estamos portanto a observar a energia do sistema que utiliza o operador de energia.
Vimos que, neste caso, a aplicaûÏûÈo do operador energûˋtico sobre o estado dûÀ simultaneamente os dois estados energûˋticos possûÙveis:
H aplicado ao | estatuto > darûÀ ou o Estado | O > (para ligar) associado com a energia El ûˋ o estado | Enl > (por nûÈo relacionado) associado com a energia Enl (as energias sûÈo os valores prû°prios do operador energûˋtico).
O operador lû°gico "ou" (ou nûÈo-exclusiva) ûˋ representado na mecûÂnica quûÂntica no espaûÏo de estado pela adiûÏûÈo dos vectores anotados " ".
Temos portanto:
H | estatuto > = O | O > Enl | Enl >
O estado global ûˋ uma sobreposiûÏûÈo dos possûÙveis eigenstatos onde El e Enl representam, como vimos, os valores energûˋticos dos dois estados respectivamente.
Para representar o facto de apenas um valor ser possûÙvel durante uma mediûÏûÈo, utilizamos uma propriedade de vectores chamada projecûÏûÈo.
Abaixo estûÀ a imagem da projecûÏûÈo do estado global |Psy> sobre o estado de energia " molûˋcula de ligaûÏûÈo" | O >
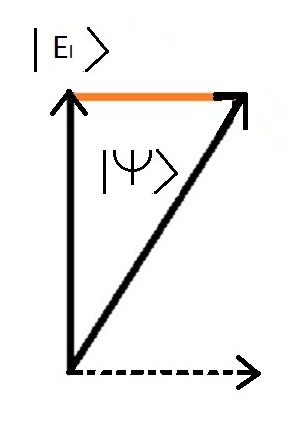 Quando a propriedade fûÙsica ûˋ medida no sistema, o postulado ûˋ que a mediûÏûÈo dûÀ um valor û¤nico e que este valor corresponde a um estado particular do sistema chamado "eigenstate", sendo o valor obtido denominado "valor prû°prio"^..
Quando a propriedade fûÙsica ûˋ medida no sistema, o postulado ûˋ que a mediûÏûÈo dûÀ um valor û¤nico e que este valor corresponde a um estado particular do sistema chamado "eigenstate", sendo o valor obtido denominado "valor prû°prio"^..
Na equaûÏûÈo anterior acrescentamos possibilidades e nûÈo valores, por isso nûÈo temos E = El Enl, adicionar um vector nûÈo funciona como adicionar um valor (escalar).
Veremos mais tarde que a adiûÏûÈo de possibilidades nûÈo conduzirûÀ û soma das energias mas ao valor mûˋdio da energia que ûˋ a soma dos valores (ici El Enl) dividido pelo nû¤mero de valores adicionados (ici 2).
O valor mûˋdio da energia seria, portanto, E = (El Enl)/2.
Na realidade ûˋ um pouco mais subtil do que isso porque o valor mûˋdio da energia tambûˋm depende da probabilidade de existûˆncia de cada estado de energia, pelo que ûˋ um valor mûˋdio ponderado pela probabilidade de cada estado.
Este ûˋ precisamente o tema do quarto postulado.
Postulat_IV
Postulado de nascimento : interpretaûÏûÈo probabilûÙstica da funûÏûÈo de onda " Ao medir a quantidade fûÙsica A num sistema em estado normalizado "phi"^, a probabilidade P (Um) para obter o valor prû°prio An do correspondente A observûÀvel ûˋ |Cn|ôý.
Onde Cn ûˋ a amplitude da funûÏûÈo da onda projectada sobre o estado eigensta |phi n> correspondente ao valor prû°prio observado An.
Atûˋ agora sû° falûÀmos de estados, estados prû°prios observûÀveis e dos seus valores prû°prios associados.
Por convenûÏûÈo, o comprimento de qualquer vector de estado ûˋ 1, sendo a razûÈo pela qual o vector de estado transmite a existûˆncia do sistema (primeira suposiûÏûÈo) e que, em termos de probabilidade, a afirmaûÏûÈo da existûˆncia do sistema corresponde a uma certeza.
Provavelmente a certeza ûˋ 1.
Quando se tem uma hipû°tese 1 em 1 de qualquer coisa (1 dividido por 1 igual a 1) estamos na certeza.
Uma probabilidade inferior a 1 ûˋ menos certa do que a certeza absoluta.
Por exemplo, a hipû°tese de ganhar a lotaria jogando apenas uma grelha ûˋ 1 dividido por alguns milhûçes.
Isto significa que no final apenas um ou quase um ganharûÀ os milhûçes no sorteio ! O sorteio em termos quûÂnticos ûˋ " a observaûÏûÈo do vencedor"^.
A amplitude da funûÏûÈo da onda ûˋ a mesma que o comprimento do vector de estado.
Vimos que um escalar ûˋ um simples valor numûˋrico.
Esta designaûÏûÈo aparece tambûˋm em comparaûÏûÈo com valores numûˋricos mais complexos compostos por vûÀrios nû¤meros, tais como o vector que, quando representado numericamente, requer a utilizaûÏûÈo de vûÀrios nû¤meros.
(se seguirmos esta linha de desenvolvimento chegamos ao conceito de "tensor" muito usado em fûÙsica, tensor de elasticidade, de curvatura do espaûÏo-tempo...Postulado IV nweb).
_
Ao projectar um vector sobre outro, o comprimento transportado do primeiro para o segundo ûˋ um nû¤mero.
RealizûÀmos assim uma operaûÏûÈo que associa um nû¤mero a dois vectores, a que chamamos escalar para indicar que o resultado particular desta operaûÏûÈo de dois vectores nûÈo dûÀ um terceiro vector como na adiûÏûÈo de vectores mas sim um nû¤mero (escalar).
Esta operaûÏûÈo ûˋ denominada produto escalar: O produto escalar ûˋ uma operaûÏûÈo que, a partir de dois vectores, dûÀ um nû¤mero.
Este nû¤mero ûˋ o comprimento ortogonalmente projectado de um vector sobre o outro.
A palavra inglesa "bracket" refere-se aos caracteres "^<" et ">" Estes parûˆnteses sûÈo tradicionalmente usados em matemûÀtica para representar o valor mûˋdio de uma quantidade. A imagem abaixo representa a projecûÏûÈo do estado geral | CûÈes > sobre os dois estados energûˋticos | CûÈes l > e | Dogs nl > (que sûÈo os mesmos que os estados | O > e | Enl > ûˋ apenas uma diferenûÏa na notaûÏûÈo)
Quando consideramos os estados " comprar pûÈo " |padeiro> e |padeiro> considerûÀmos implicitamente que podûÙamos observar um e outro de forma indiferente, ou seja, com uma probabilidade de ocorrûˆncia igual.
"A soma do quadrado do comprimento dos dois lados ûˋ igual ao quadrado do comprimento da hipotenusa"^ No nosso caso, a hipotenusa corresponde ao vector de estado |phi> e de ambos os lados para o |phi> sobre os dois estados-membros |padeiro> e | Epicier>. Se considerarmos a expressûÈo | CûÈes L >< CûÈes L | composto por um ket e um soutien e aplicado ao ket | CûÈes > obtemos | CûÈes L >< CûÈes L | CûÈes > onde < CûÈes L | CûÈes > ûˋ a amplitude da probabilidade de obter o estado | CûÈes L > por isso temos : | CûÈes L >< CûÈes L | CûÈes > = | CûÈes L > Al = Al | CûÈes L > vemos que o estado final ûˋ o | CûÈes L > associado com a probabilidade Al A expressûÈo | CûÈes L >< CûÈes L | ûˋ portanto um operador que mudou o estado inicial | CûÈes > para o estado final | CûÈes L > e isto com uma probabilidade Al.
1.2.2.Divisû°ria do operador da unidade
Considere o seguinte operador:
| CûÈes L >< CûÈes L | | Dogs nl >< Dogs nl | que ûˋ a soma dos operadores da evoluûÏûÈo em direcûÏûÈo aos egocentrismos de um observûÀvel (aqui a energia : estado vinculado e nûÈo vinculado).
û interessante notar como a representaûÏûÈo vectorial do estado e a sua decomposiûÏûÈo de acordo com uma base ortogonal permite representar naturalmente as amplitudes das probabilidades e assim as probabilidades da evoluûÏûÈo do sistema durante uma mediûÏûÈo.
Postulat_V
Medida : reduûÏûÈo de pacotes de ondas Se a mediûÏûÈo da quantidade fûÙsica A, no tempo t, sobre um sistema representado pelo vector |phi> resulta no valor prû°prio e depois o estado do sistema imediatamente apû°s a mediûÏûÈo ser projectado no espaûÏo prû°prio associado a um Este postulado tambûˋm ûˋ chamado de postulado de reduûÏûÈo de pacotes "^wave..
û provavelmente a maior revoluûÏûÈo conceptual da mecûÂnica quûÂntica introduzir o facto de que a observaûÏûÈo do sistema o faz evoluir, enquanto nas teorias fûÙsicas nûÈo quûÂnticas ûˋ apenas a equaûÏûÈo dinûÂmica que ûˋ responsûÀvel pela evoluûÏûÈo do sistema.
Tradicionalmente, a equaûÏûÈo dinûÂmica de uma teoria mecûÂnica expressa como a energia actua sobre o sistema para o transformar.
L_expûˋrience_du_chat_de_Shroedinger ûˋ uma experiûˆncia de pensamento idealizada pelo fûÙsico Erwin_Shroedinger reflectir sobre o problema da mediûÏûÈo em mecûÂnica quûÂntica directamente relacionada com o quinto postulado.
Note a ligaûÏûÈo entre o observador e a funûÏûÈo de onda: nenhum dos quais ûˋ material ! Poder-se-ia dizer que o que ûˋ material ûˋ o que estûÀ entre os dois: observaûÏûÈo.
A funûÏûÈo da onda e a consciûˆncia representam dois lados da mesma realidade transcendendo a materialidade e
na prû°pria origem desta materialidade.
obviamente os fûÙsicos como um todo nûÈo vûÈo tûÈo longe na sua visûÈo da realidade quûÂntica.
A posiûÏûÈo padrûÈo nesta ûÀrea ûˋ ainterprûˋtation_de_l_ûˋcole_de_Copenhague.
Esta posiûÏûÈo emerge da situaûÏûÈo do observador humano que experimenta um mundo clûÀssico e o considera como a referûˆncia absoluta.
Podem ser definidos diferentes graus de distûÂncia a partir desta posiûÏûÈo:
û de notar que este ponto de vista jûÀ nûÈo ûˋ cientificamente defensûÀvel desde a experiûˆncia da Aspect, que valida a mecûÂnica
nas suas declaraûÏûçes mais perturbadoras.
Ao mesmo tempo, esta mecûÂnica quûÂntica ûˋ a teoria mais verificada na histû°ria da ciûˆncia.
Este ponto de vista ûˋ assim reduzido a uma simples crenûÏa "materialista "^.
Esta visûÈo era, no entanto, de Einstein, mas infelizmente ele nûÈo viveu tempo suficiente para
ver a resoluûÏûÈo da experiûˆncia Aspect do paradoxo que definiu com os fûÙsicos Podolsky e Rosen no seu famoso artigo:
o Paradoxe_EPR.
Aqui o mundo clûÀssico em que vivemos jûÀ nûÈo representa a totalidade do mundo porque hûÀ
um mundo quûÂntico absolutamente estranho ao qual nûÈo temos acesso mas com o qual podemos lidar
atravûˋs da teoria quûÂntica.
O mundo fûÙsico estûÀvel que conhecemos ûˋ constituûÙdo apenas por trûˆs partûÙculas quûÂnticas: electrûÈo, prû°ton e neutrino.
Este terceiro ponto de vista elimina todos os paradoxos quûÂnticos ao dizer, finalmente e de forma simples, que nûÈo devemos
nûÈo procurar uma interpretaûÏûÈo (clûÀssico) da teoria quûÂntica, mas que se tem simplesmente de a aceitar
como ûˋ (Copenhague) e finalmente reconhecer a supremacia da sua posiûÏûÈo.
Pode assim prever-se que o modelo quûÂntico nunca serûÀ defeituoso. Desde o seu inûÙcio, tem vindo a tornar-se cada vez mais claro como a realidade quûÂntica
intervûˋm na compreensûÈo do mundo que nos rodeia e mais particularmente no campo da vida, um sistema macroscû°pico de grande coerûˆncia... quantum.
Dois exemplos bastante recentes sûÈo:
Postulat_VI evoluûÏûÈo temporal do estado quûÂntico. _ H |Phi(t)> = i h/2*pi d |Phi(t)> / dt _
0,000000000000000000000000000000000662607004 Quando esta constante ûˋ combinada com outras constantes fundamentais como a velocidade da luz ou a constante gravitacional universal, as quantidades mûÙnimas das diferentes unidades da fûÙsica podem ser deduzidas : Comprimento Planck, tempo Planck, etc....
1.5.ExpressûÈo poûˋtica condensada de postulados
O que se segue ûˋ uma tentativa de combinar todas as hipû°teses num û¤nico aforismo:
" O que ûˋ possûÙvel realiza-se, sob o olhar da consciûˆncia, sû° se realiza o que ûˋ possûÙvel.
A mecûÂnica quûÂntica ûˋ a maior revoluûÏûÈo da nossa era cientûÙfica moderna porque destrû°i definitivamente a posiûÏûÈo materialista, abrindo assim o caminho para um desenvolvimento da humanidade onde a ciûˆncia e a consciûˆncia estarûÈo novamente unidas.
A experiûˆncia decisiva que permitiu resolver o paradoxo Einstein-Podolski-Rosen, levada a cabo em 1982 pelo investigador e experimentador Alain Aspect
no centro de û°ptica quûÂntica de Orsay era baseado em fotûçes.
Uma descriûÏûÈo detalhada da teoria subjacente pode ser encontrada em
O livro de Bernard d'Espagnat " A la recherche du rûˋel"^ .
Nesse mesmo ano, eu estava na universidade e o Alain Aspect estava
veio apresentar os seus resultados em Toulouse, no anfiteatro Maxwell da Universidade
Paul Sabatier.
O anfiteatro era composto por trûˆs baûÙas separadas por duas escadas. O
A maior baûÙa central estava cheia de fûÙsicos e outros
cientistas de todo o campus da Rangueil. Nas outras bancadas, nûÈo havia ninguûˋm ! Foi
muito curioso porque os que se encontravam no fundo da sala podiam ver
menos bem do que se se tivessem aproximado nas baûÙas laterais. Cela
Diverti-me porque sabia porque era assim, mas foi quando
mesmo impressionante. O que estava prestes a ser-lhes anunciado seria como um golpe na cabeûÏa.
Depois de apresentar resultados de mediûÏûÈo inequûÙvocos, ele
deixou a assembleia sem palavras (a sala de conferûˆncias estava cheia de professores e estudantes.
de investigadores) .
No final da apresentaûÏûÈo, apû°s um longo momento de silûˆncio,
significativo quando o piso foi dado a uma assembleia de cientistas, um
o investigador levantou-se (o meu professor de relatividade na altura Alain Gautier) e posou
esta pergunta:
" E achas fûÀcil viver com isso agora? " .
Aspect, na defensiva, respondeu que nûÈo o tinha dito, que o tinha feito
uma experiûˆncia e que o resultado foi esse, mas que ele teve o cuidado de nûÈo
dar qualquer interpretaûÏûÈo.
Aprendi anos mais tarde, com alguûˋm que tinha estado com ele, que ele
era prû°-Einsteiniano e que ele esperava uma mecûÂnica quûÂntica
falharia.
Eu estava numa baûÙa lateral na terceira fila, sozinho e estava
Diverti-me porque nûÈo percebia porque ûˋ que eles tinham um problema com isso, ou porque ûˋ que nûÈo sabiam o que fazer.
compreendi-o bem demais.
Quando a experiûˆncia estava na sua fase inicial mas o resultado nûÈo era claro, a
mais do que uma questûÈo de tempo, a controvûˋrsia tornou-se muito forte, mesmo sulfurosa.
Eu tinha visto um artigo na popular revista Science
que apresentou uma contra-experimentaûÏûÈo û experiûˆncia da Aspect conduzida por um fûÙsico italiano
que disse que se a experiûˆncia Aspect confirmasse a mecûÂnica quûÂntica, entûÈo
deixaria de estudar fûÙsica porque isso jûÀ nûÈo faria sentido para ele. NûÈo sei se ele tem
manteve a sua palavra.
Quando a comunidade cientûÙfica dos fûÙsicos estava em estado de choque,
poderia perguntar-se o que iria acontecer.
Levou tempo para que a informaûÏûÈo fosse digerida, como se pode ver em
2020 que a situaûÏûÈo mudou significativamente, basta olhar para
Esta conferûˆncia proferida na Ecole Polytechnique por Hervûˋ Zwirn, Director de
investigaûÏûÈo no CNRS
_x_sciences_de_l_homme_et_de_la_sociûˋtûˋ_x_shs_mûˋcanique_quantique_le_monde_existe_t_il
Esta experiûˆncia tem tido (ou deveria ter tido para a maioria) do mesmo tipo
na comunidade fûÙsica que a descoberta do
ondes deerziennes (ondas electromagnûˋticas) que deram o conceito abstracto de
campo electromagnûˋtico uma realidade muito mais vûÙvida. A descoberta do
nûÈo separabilidade e a sua observaûÏûÈo a nûÙvel fûÙsico dûÀ vida ao conceito de
realidade independente, ou seja, uma realidade que ûˋ independente do espaûÏo e do tempo, ou seja
de todas as contingûˆncias espaûÏo-temporais, ou seja, de todas
todas as contingûˆncias fûÙsicas.
Uma primeira conclusûÈo que pode ser extraûÙda do primeiro postulado de
mecûÂnica quûÂntica ûˋ que:
A realidade de um sistema quûÂntico (e, no final, todos os sistemas sûÈo quûÂnticos! )
ûˋ sustentado por um espaûÏo abstracto de possibilidades que ûˋ inobservûÀvel em si (
nûÈo-fûÙsico e independente de todas as contingûˆncias espaûÏo-temporais) mais
no entanto real, uma vez que ûˋ a partir deste nûÙvel de funcionamento abstracto que o
a realidade concreta (observado) .
Para resumir em uma palavra: trata-se de omnipresenûÏa e omnisciûˆncia
uma vez que contûˋm toda a informaûÏûÈo sobre o sistema fûÙsico de uma forma que ûˋ
nûÈo-local.
Alûˋm disso, para ser exaustivo, isto estûÀ relacionado com o observador que nûÈo
pode obviamente ser fûÙsico. Os pressupostos obviamente nûÈo incluem o observador
no sistema fûÙsico, mas declara a sua existûˆncia necessûÀria para
uma observaûÏûÈo tem lugar ou ûˋ produzido um resultado fûÙsico.
û û°bvio que o observador e o
a realidade independente tem uma relaûÏûÈo estreita: sûÈo ambos nûÈo-fûÙsicos
e interagir em termos de informaûÏûÈo, conhecimento, percepûÏûÈo. Isto
encaixa perfeitamente nas concepûÏûçes dos xamûÈs sobre o " sonho do mundo"^..
A este respeito, o filme Matrix pode ser visto como uma alegoria de
realidade quûÂntica. A diferenûÏa com a realidade ûˋ que a
A simulaûÏûÈo hologrûÀfica do mundo nûÈo ûˋ feita por computadores de hardware, mas por
um computador cû°smico nûÈo-material que se identifica com a consciûˆncia no seu
desenho mais extensivo.
Podemos e demos a esta consciûˆncia universal toda a
nomes como se deseja, mas estes nunca esgotarûÈo o poder infinito de
esta SensibilizaûÏûÈo.
O valor mûˋdio da energia serûÀ notado, por exemplo < E >.
Vimos que o estado quûÂntico tambûˋm ûˋ chamado de "ket" anotado | ket > a outra parte do parûˆntesis ûˋ o "bra" que ûˋ um operador particular notado < bra | û o fûÙsico Paul_Dirac que estûÀ na origem desta separaûÏûÈo em duas desta palavra para fazer aparecer uma dinûÂmica de operador e vector na operaûÏûÈo de tomar o valor mûˋdio.
Se aplicarmos o "bra" ao ^cket"^, obtemos < bra | ket > que ûˋ o nû¤mero que resulta da aplicaûÏûÈo do operador
Aqui temos uma relaûÏûÈo dupla entre soutien e ket.
Para um Estado (ou ket) "| CûÈes >^ le bra sera "^< CûÈes |" a dualidade entre os dois ûˋ representada como a imagem num espelho O ket ûˋ um vector enquanto o soutien ûˋ um operador, aplicando o soutien ao ket dûÀ um nû¤mero.
Em geral, numa expressûÈo o que estûÀ û direita do ket ûˋ um operador, o resultado de um operador sobre um estado (vector) ou ûˋ outro estado (vector) ou um nû¤mero que representa um resultado de mediûÏûÈo ou uma probabilidade.
Para cada ket existe um soutien correspondente e a operaûÏûÈo que permite passar do ket ao soutien ûˋ chamada conjugaûÏûÈo hermûˋtica e ûˋ notada por uma estrela.
Assim ( | CûÈes > ) * = < CûÈes | ou (
Isto pode ser analogamente relacionado com um aforismo vûˋdico em que o criador do universo fala: " virando-me contra mim mesmo, eu crio de novo e de novo".
A mesma forma tambûˋm pode ser vista na primeira histû°ria de criaûÏûÈo do Gûˋnesis: que haja luz e houvesse luz e D.
Deus viu que a luz era boa.
< que haja luz | e a luz era > = e D.
Deus viu que a luz era boa.
< ou | luzôý. | barril > = D.
Deus viu que a luz era boa.
O facto de D.
Deus viu que a luz era boa ûˋ claramente o resultado de uma observaûÏûÈo.
PoderûÙamos chamar a tudo isto o alfabeto quûÂntico e a sintaxe.
O alfabeto ûˋ composto por apenas uma letra | CûÈes > e isso ûˋ " o ser" (ou o estado que ûˋ a afirmaûÏûÈo do ser) A operaûÏûÈo dupla * mostra o seu valor de operador dinûÂmico ( | CûÈes > )* = < CûÈes | Todas as suas combinaûÏûçes dûÈo origem û gramûÀtica quûÂntica.
Um exemplo ûˋ a aplicaûÏûÈo do operador < CûÈes | sobre o estado | CûÈes > dûÀ < Psy|CûÈes > que ûˋ tambûˋm a projecûÏûÈo do |Psy> sobre si mesma e ûˋ portanto 1.
Isto pode ser traduzido trivialmente na seguinte frase: "Psy participa a 100%. (100/100=1) para Psy".
< CûÈes L | CûÈes > ûˋ a projecûÏûÈo do estado geral do sistema sobre o estado de energia limite do exemplo da molûˋcula H2 e representa a amplitude da probabilidade de obter o estado limite durante uma observaûÏûÈo.
Al = < CûÈes L | CûÈes > Tomar o quadrado da amplitude dûÀ a probabilidade A probabilidade do estado | CûÈes L > ûˋ: Pl = Alôý = ( < CûÈes L | CûÈes > )ôý 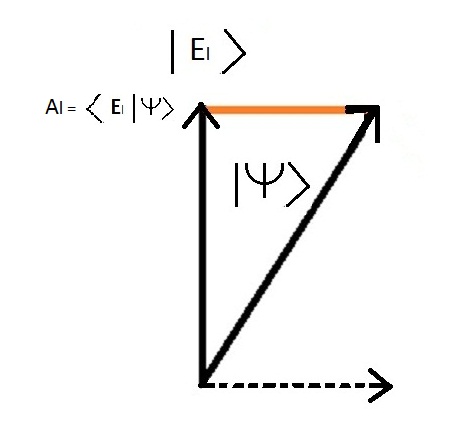
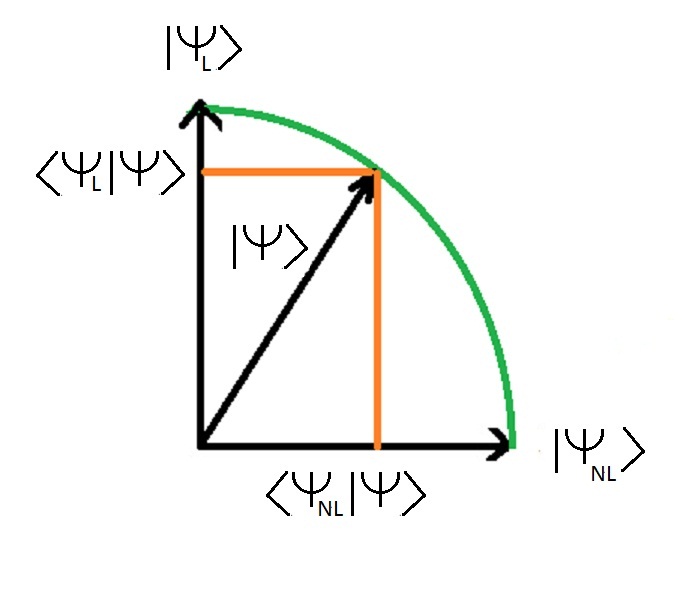 Os dois valores < CûÈes l | CûÈes > e < Dogs nl | CûÈes > sûÈo o comprimento do estado | CûÈes > (que ûˋ 1) projectado nas prû°prias declaraûÏûçes | CûÈes l > e | Dogs nl > < CûÈes l | CûÈes > ûˋ a projecûÏûÈo do estado | CûÈes > sobre o estado limpo | CûÈes l > < Dogs nl | CûÈes > ûˋ a projecûÏûÈo do estado | CûÈes > sobre o estado limpo | Dogs nl >
Os dois valores < CûÈes l | CûÈes > e < Dogs nl | CûÈes > sûÈo o comprimento do estado | CûÈes > (que ûˋ 1) projectado nas prû°prias declaraûÏûçes | CûÈes l > e | Dogs nl > < CûÈes l | CûÈes > ûˋ a projecûÏûÈo do estado | CûÈes > sobre o estado limpo | CûÈes l > < Dogs nl | CûÈes > ûˋ a projecûÏûÈo do estado | CûÈes > sobre o estado limpo | Dogs nl >
Isto ûˋ conhecido como um estado equiprobûÀvel.
Mas as caracterûÙsticas do sistema podem ser tais que nûÈo ûˋ esse o caso, por exemplo, se o padeiro estiver mais perto de casa do que o pasteleiro e estiver muito frio a probabilidade do estado |padeiro> serûÀ mais forte do que a do Estado |padeiro>.
Isto ûˋ representado na imagem abaixo onde Ab ûˋ maior que Ap.
(A ûˋ a amplitude da probabilidade).
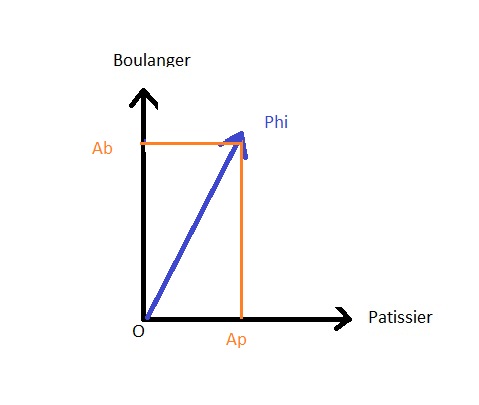 A projecûÏûÈo do Estado |Phi> geral sobre o estado |padeiro> tem o valor Ab que corresponde û amplitude de probabilidade de obter este estado do estado geral |Phi> O mesmo se aplica ao Ap que ûˋ a amplitude da probabilidade de obter o estado |padeiro>.
A projecûÏûÈo do Estado |Phi> geral sobre o estado |padeiro> tem o valor Ab que corresponde û amplitude de probabilidade de obter este estado do estado geral |Phi> O mesmo se aplica ao Ap que ûˋ a amplitude da probabilidade de obter o estado |padeiro>.
Os autoestados quûÂnticos sûÈo sempre ortogonais, ou seja, estûÈo em ûÂngulo recto uns com os outros e, portanto, seguem a . Pythagore
para o triûÂngulo em ûÂngulo recto.
O postulado diz que o quadrado da amplitude da onda ûˋ a probabilidade.
Considerando o estado geral do sistema significa simplesmente considerar que hûÀ: a probabilidade do estado real do sistema ûˋ portanto sempre igual a 1.
Isto ûˋ o que o postulado menciona ao dizer que o Estado |phi> ûˋ normalizada e a sua norma ûˋ sempre igual a 1 por convenûÏûÈo, uma vez que ûˋ uma probabilidade.
Matematicamente, notamos < phi | phi > = 1 = | |phi> | ôý (a û¤ltima expressûÈo representa o quadrado da norma do vector, sendo a norma do vector o seu comprimento) EntûÈo esta probabilidade ûˋ dividida em vûÀrias probabilidades mais baixas correspondentes a cada eigenstate mas com a restriûÏûÈo de que a soma dos quadrados das amplitudes dos eigenstatos do sistema ûˋ sempre igual a 1 que ûˋ a probabilidade certa.
No nosso caso, temos:
Abôý Apôý = 1 A soma das probabilidades de todos os estados possûÙveis do sistema deve ser igual a 1.
Pode dizer-se que a existûˆncia do sistema estûÀ espalhada por todas as suas possibilidades de existûˆncia mas sem qualquer perda de existûˆncia para que a sua existûˆncia seja preservada.
Com efeito, se a probabilidade total diminuûÙsse, isso significaria que o sistema teria menos hipû°teses de existir e, ao reduzir a probabilidade da sua existûˆncia a zero, desapareceria ! A amplitude do estado ou funûÏûÈo de onda pode ser positiva ou negativa tal como o pico ou a calha de uma onda.
A amplitude da probabilidade ûˋ portanto negativa ou positiva, que ûˋ o que representamos na imagem dos estados de ligaûÏûÈo e nûÈo ligaûÏûÈo da molûˋcula de hidrogûˋnio atravûˋs dos sûÙmbolos mais e menos - .
(. ûˋtats molûˋcule hydrogû´ne PitûÀgoras) Mas a probabilidade que ûˋ o quadrado da amplitude (ou quadrado da norma ) ûˋ, portanto, sempre positivo, o que ûˋ normal para uma probabilidade.
De facto, podemos imaginar uma certa probabilidade, depois uma menos certa, depois uma incerta ou mesmo uma zero, mas uma probabilidade negativa nûÈo tem sentido..
Por outro lado, a amplitude da probabilidade pode ser negativa.
Suponha entûÈo que temos duas amplitudes de probabilidade iguais, mas de sinais opostos que se propagam um para o outro (sûÈo ondas).
Se considerarmos as probabilidades quando estas amplitudes estûÈo no mesmo lugar, entûÈo as amplitudes dos sinais opostos anulam-se e o seu quadrado tambûˋm ûˋ zero.
A probabilidade de observar algo serûÀ zero.
Mas se as amplitudes forem separadas, o seu quadrado serûÀ positivo (mais por mais ûˋ positivo mas menos por menos tambûˋm ûˋ positivo) e, portanto, a probabilidade de observar algo jûÀ nûÈo serûÀ zero.
Quando falamos de mecûÂnica quûÂntica pensamos no seu carûÀcter probabilûÙstico como um jogo de azar, mas o que geralmente ignoramos ûˋ que estas probabilidades sûÈo sustentadas por algo muito mais perturbador, que ûˋ a amplitude da onda de probabilidade e que dûÀ û mecûÂnica quûÂntica a sua realidade.
û um operador de evoluûÏûÈo que fez o sistema evoluir para o estado de energia ligado durante uma observaûÏûÈo.
Isto leva-nos naturalmente ao quinto postulado que descreve como o sistema evolui durante uma mediûÏûÈo.
Se aplicarmos este operador ao ket | CûÈes > sobre um :
( | CûÈes L >< CûÈes L | | Dogs nl >< Dogs nl | ) | CûÈes > ou | CûÈes L >< CûÈes L | CûÈes > | Dogs nl >< Dogs nl | CûÈes > o que resulta em | CûÈes L > Al | Dogs nl > Anl ou mesmo Al | CûÈes L > Anl | Dogs nl > que ûˋ a decomposiûÏûÈo do estado | CûÈes > em soma dos seus prû°prios estados energûˋticos | CûÈes > = Al | CûÈes L > Anl | Dogs nl > O operador nûÈo alterou o estado | CûÈes > mas simplesmente o decompûÇs nas suas partes individuais, por esta razûÈo ûˋ chamado de " operador da divisû°ria "unit.
Antes de mais, esclareûÏamos esta noûÏûÈo de "sub-espaûÏo prû°prio"^.
Trata-se apenas de uma generalizaûÏûÈo da decomposiûÏûÈo do Estado nos seus prû°prios Estados.
Voltemos ao exemplo do pûÈo com dois padeiros e um pasteleiro.
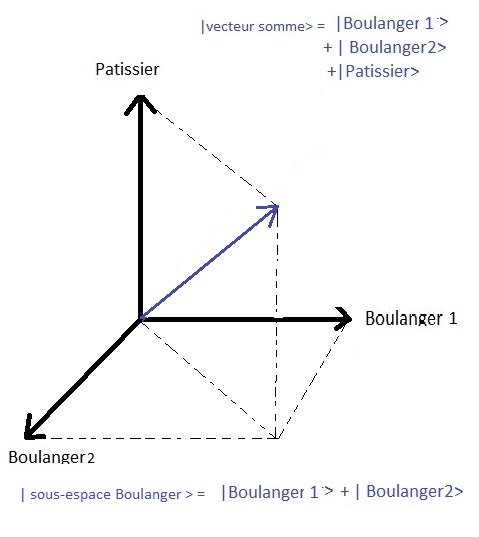
Se a distinûÏûÈo do tipo de comûˋrcio nûÈo for observûÀvel (nûÈo ûˋ um sistema observûÀvel)No caso de uma mediûÏûÈo, nûÈo haverûÀ necessidade de distinguir se ûˋ padeiro 1 ou padeiro 2, serûÀ suficiente saber que o estado foi projectado para o subespaûÏo do prû°prio padeiro, o que corresponde, de facto, no diagrama abaixo, ao plano horizontal povoado pelos padeiro ! Se houvesse um observûÀvel que nos permitisse observar de que padeiro o pûÈo foi comprado, durante esta mediûÏûÈo o estado seria projectado para um ou outro dos padeiros, levantando a indeterminaûÏûÈo da mediûÏûÈo.
Mas se esta propriedade do sistema nûÈo for observada, entûÈo o sistema permanece neste estado de sobreposiûÏûÈo das funûÏûçes da onda panificadora.
Diz-se que o estado ûˋ degenerado.
Na prûÀtica, quando vûÀrios Estados Membros tûˆm o mesmo valor prû°prio (a mesma energia) disseram que estes estados sûÈo degenerados.
Ao aplicar uma restriûÏûÈo energûˋtica adicional ao sistema que irûÀ alterar a energia dos estados degenerados para que nûÈo haja mais igualdade, a degenerescûˆncia serûÀ removida.
A fûÙsica quûÂntica estûÀ essencialmente preocupada em compreender a estrutura do mundo microscû°pico que ûˋ essencialmente composto por ressonûÂncias (ondas em pûˋ) que sûÈo os estados prû°prios do operador total de energia do sistema (Hamiltonien).
 O quinto postulado afirma que, durante a mediûÏûÈo, o estado do sistema evolui para o estado cujo valor prû°prio foi medido.
O quinto postulado afirma que, durante a mediûÏûÈo, o estado do sistema evolui para o estado cujo valor prû°prio foi medido.
û este chamado postulado de " reduûÏûÈo de pacotes de ondas " ou "colapso da funûÏûÈo de onda"^ que dûÀ û representaûÏûÈo geomûˋtrica de uma projecûÏûÈo vectorial a sua realidade fûÙsica, uma vez que o sistema evolui fisicamente nesta operaûÏûÈo.
Neste quinto postulado, vimos que a prû°pria mediûÏûÈo transforma o sistema.
No caso da mecûÂnica quûÂntica, tal equaûÏûÈo dinûÂmica tambûˋm existe e ûˋ chamada a equaûÏûÈo de Shroedinger .
Na mecûÂnica, existem portanto dois mecanismos de evoluûÏûÈo: a acûÏûÈo da energia no tempo e a acûÏûÈo da observaûÏûÈo fora do tempo.
û esta equaûÏûÈo que constitui o sexto e û¤ltimo postulado da mecûÂnica quûÂntica (ver abaixo).
O quinto postulado envolve o observador do sistema na evoluûÏûÈo do sistema.
Assim, na mecûÂnica quûÂntica, o observador jûÀ nûÈo ûˋ independente do sistema fûÙsico.
O observador e o sistema fûÙsico formam um todo inseparûÀvel.
Poder-se-ia dizer que o observador estûÀ embutido no sistema (mas nûÈo no sentido de emaranhamento quûÂntico, que apenas diz respeito û funûÏûÈo de onda).
MencionûÀmos acima o fenû°meno do enredamento quûÂntico, que resulta do facto de um sistema quûÂntico composto por vûÀrias partûÙculas ser descrito por uma û¤nica funûÏûÈo de onda (primeira suposiûÏûÈo) mesmo que seja provûÀvel que as partûÙculas se tenham deslocado no espaûÏo fûÙsico.
De acordo com o quinto postulado, durante uma mediûÏûÈo a funûÏûÈo de onda colapsa para um subespaûÏo adequado, afectando instantaneamente ao mesmo tempo o estado de todas as partûÙculas que compûçem o sistema.
Foi esta implicaûÏûÈo da mecûÂnica quûÂntica que Einstein nunca pûÇde admitir oficialmente porque, na sua opiniûÈo, violava o limite de propagaûÏûÈo de qualquer interacûÏûÈo fûÙsica definida pela velocidade da luz.
De acordo com a teoria da relatividade de Einstein, nenhuma energia pode viajar mais depressa do que a velocidade da luz.
A luz viaja obviamente û velocidade da luz e sû° o pode fazer porque ûˋ energia pura, ou seja, sem massa.
As partûÙculas de massa devem, portanto, deslocar-se necessariamente a uma velocidade inferior û velocidade da luz.
A resoluûÏûÈo "fûÙsica" deste paradoxo quûÂntico foi realizada por uma experiûˆncia conhecida como aexpûˋrience_d_Aspect.
Esta experiûˆncia provou indiscutivelmente que a funûÏûÈo de onda nûÈo depende do espaûÏo fûÙsico em que vivemos: a sua evoluûÏûÈo durante o colapso devido û observaûÏûÈo tem lugar em qualquer ponto do espaûÏo ao mesmo tempo.
A experiûˆncia da Aspect tem sido replicada muitas vezes em condiûÏûçes cada vez mais sofisticadas para levar a mecûÂnica quûÂntica aos seus limites, mas nunca cedeu em ! Diz-se que a teoria quûÂntica ûˋ uma teoria nûÈo-local.
Os termos usados "nûÈo-localidade" ou "nûÈo-separabilidade"^ sûÈo equivalentes.
Podemos portanto dizer que a funûÏûÈo de onda quûÂntica transcende o espaûÏo fûÙsico, transcende mesmo o espaûÏo-tempo desde a teoria da relatividade de Einstein que devemos considerar o espaûÏo e o tempo como aspectos da mesma realidade mais profunda : o continuum espaûÏo-tempo.
Uma experiûˆncia mais recente realizada num quadro relativista e no seguimento da experiûˆncia da Aspect confirmou a validade do enredamento quûÂntico no quadro relativista.
( cf Expûˋrience_d_Antoine_Suarez encontrado no website do fûÙsico Philippe_Guillemant que oferece uma visûÈo integrando a realidade quûÂntica ) Esta û¤ltima experiûˆncia ûˋ importante porque numa experiûˆncia de fûÙsica sû° se pode medir valores dentro de um determinado intervalo.
Assim, na primeira experiûˆncia Aspect, os detectores de fû°tons correlacionados (num û¤nico estado quûÂntico) estavam apenas a alguns metros de distûÂncia.
Isto foi suficiente para demonstrar que o enredamento quûÂntico nûÈo podia ser devido a um fenû°meno fûÙsico desconhecido (variûÀvel oculta) û velocidade sub-luminosa.
A velocidade de um tal fenû°meno seria necessariamente superluminal.
Embora tal velocidade superluminal seja dificilmente aceitûÀvel devido û teoria da relatividade de Einstein, a primeira experiûˆncia da Aspect nûÈo descartou completamente esta possibilidade.
Com a experiûˆncia de Antoine Suarez isto ûˋ feito porque ûˋ mesmo a possibilidade de uma causalidade entre as detecûÏûçes dos dois fotûçes correlacionados que ûˋ suprimida, porque os quadros de referûˆncia relativistas em que as detecûÏûçes sûÈo feitas, nûÈo permitem um " antes" e " depois", uma condiûÏûÈo essencial para a causalidade: nenhum dos fû°tons ûˋ detectado antes ou depois do outro porque estas detecûÏûçes nûÈo sûÈo feitas no mesmo perûÙodo de tempo.
Numa teoria quûÂntica relativista, a funûÏûÈo das ondas jûÀ nûÈo pode, portanto, depender do tempo, como vimos no primeiro postulado.
A razûÈo ûˋ que o tempo ûˋ reduzido para o mesmo nûÙvel da posiûÏûÈo, ou seja, uma propriedade observûÀvel do sistema, e a funûÏûÈo de onda ûˋ independente das propriedades do sistema (segunda premissa).
Numa tal teoria, a funûÏûÈo de onda seria | CûÈes > e jûÀ nûÈo | Psy(t) > .
O tempo seria um T observûÀvel, da mesma forma que a posiûÏûÈo P.
A particularidade desta experiûˆncia de pensamento completamente irrealista tal como apresentada com um " gato real" ûˋ fazûˆ-lo pensar sobre o que o observador ûˋ na mecûÂnica quûÂntica.
Viu nos postulados sobre a medida (ou observaûÏûÈo) que nûÈo entremos em detalhes sobre o que ûˋ o observador.
Os postulados dizem que hûÀ um observador que faz a mediûÏûÈo mas nada mais diz sobre a natureza do observador ! Nesta experiûˆncia, um gato ûˋ isolado numa caixa para que nûÈo possa ser observado (quantificado) de qualquer forma.
Isto pressupûçe que o gato pode ser considerado como um objecto quûÂntico, o que nûÈo ûˋ o caso na prûÀtica, embora em teoria o gato possa ser considerado a priori como um sistema fûÙsico, sendo composto por ûÀtomos que sûÈo e sûÈo bem descritos pela mecûÂnica quûÂntica.
Nesta cûÂmara hûÀ tambûˋm um frasco contendo um gûÀs que ûˋ mortal para o gato e um detector de partûÙculas que abre o frasco se for detectada uma partûÙcula.
Se uma partûÙcula for detectada, o gato estarûÀ morto, se nûÈo for detectada, o gato estarûÀ vivo.
Enquanto nûÈo tivermos observado o estado de saû¤de do gato "quûÂntico", ele permanece num estado quûÂntico geral conhecido como a sobreposiûÏûÈo de eigenstatos observûÀveis, que sûÈo | gato vivo > e | chat mort > por isso temos | chat > = | gato vivo > | chat mort > O nosso sistema quûÂntico ûˋ constituûÙdo por vûÀrios componentes: o gato, o detector, a partûÙcula.
Todos estes subsistemas devem tambûˋm ser considerados no estabelecimento da funûÏûÈo de onda, pelo que temos: | partûÙcula > = | partûÙcula presente > | partûÙcula ausente > e | sensor > = | partûÙcula de estado detectada > | estado de partûÙculas nûÈo detectadas > A matemûÀtica associada û mecûÂnica quûÂntica mostra que o sistema global a que chamaremos "shroedinger"^ ûˋ : | shroedinger > = | gato, detector, partûÙcula > = | chat> ôÊ | sensor > ôÊ | partûÙcula > onde ôÊ ûˋ o produto "tensor ^ dos vectores estatais.
Uma vez que se encontram no mesmo estado quûÂntico, diz-se que estes diferentes subsistemas sûÈo intrincados.
Este produto comporta-se como uma transacûÏûÈo de produto regular, ûˋ distributivo : A * ( B C ) = A*B A*C Em termos quûÂnticos podemos, portanto, desenvolver o estado quûÂntico geral.
Comecemos apenas pelo sistema constituûÙdo apenas pelo detector e pela partûÙcula.
| detector, partûÙcula > = | sensor > ôÊ | partûÙcula > = ( | partûÙcula de estado detectada > | estado de partûÙculas nûÈo detectadas > ) ôÊ ( | partûÙcula presente > | partûÙcula ausente > ) desenvolvendo :
| detector, partûÙcula > = | partûÙcula de estado detectada > ôÊ | partûÙcula presente >
| estado de partûÙculas nûÈo detectadas > ôÊ | partûÙcula ausente >
| estado de partûÙculas nûÈo detectadas > ôÊ | partûÙcula presente >
| partûÙcula de estado detectada > ôÊ | partûÙcula ausente >
Erwin Shroedinger nweb Os dois primeiros estados sûÈo facilmente compreendidos, se a partûÙcula estiver presente ûˋ lû°gico que seja detectada e se nûÈo estiver presente nûÈo ûˋ detectada.
Os dois estados seguintes sûÈo altamente improvûÀveis, mas no entanto existem de acordo com a mecûÂnica quûÂntica, para a qual tudo ûˋ apenas uma amplitude de probabilidade.
Para o Estado | shroedinger > completar seria necessûÀrio desenvolver mais com os estados do gato, o que nos levaria a uma funûÏûÈo de onda com oito possûÙveis eigenstatos, dois dos quais sûÈo altamente provûÀveis e seis altamente improvûÀveis.
Os dois estados provûÀveis sûÈo:
| chat mort > ôÊ | partûÙcula de estado detectada > ôÊ | partûÙcula presente > | gato vivo > ôÊ | estado de partûÙculas nûÈo detectadas > ôÊ | partûÙcula ausente > Enquanto nûÈo tivermos observado o sistema, que corresponde, por exemplo, û abertura da caixa, estamos num estado de sobreposiûÏûÈo em que o gato estûÀ num estado vital indeterminado.
Aqui reside o paradoxo.
Mas podemos levar o raciocûÙnio mais longe e foi isto que o fûÙsico fez Eugû´ne_Wigner Prûˋmio Nobel da FûÙsica.
Este ûˋ o thûˋorie_de_l_influence_de_la_conscience Ele considerou que o olho do observador que vûˆ o gato morto ou vivo ûˋ tambûˋm um sistema quûÂntico com dois estados: | oeil > = | o olho vûˆ o gato morto > | o olho vûˆ o gato vivo > Os estados da funûÏûÈo de onda completa teriam entûÈo em conta " estados alucinû°genos " onde o olho veria morto, o gato vivo...
Mas poderûÙamos continuar a considerar a cadeia de medida atûˋ ao cûˋrebro do observador, que tambûˋm ûˋ composto por ûÀtomos.
Assim, a questûÈo ûˋ : quando a mediûÏûÈo ûˋ realmente realizada, ou seja, o colapso da funûÏûÈo de onda e, portanto, a escolha do resultado da experiûˆncia: gato vivo ou morto.
Wigner diz que nada material pode causar colapso porque toda a materialidade ûˋ susceptûÙvel de descriûÏûÈo pela mecûÂnica quûÂntica e, portanto, faz parte da funûÏûÈo de onda e tambûˋm se pode considerar muito bem a funûÏûÈo de onda do universo.
Se nada material opera a mediûÏûÈo, resta apenas algo imaterial que o faz, e este Wigner identifica-se com a consciûˆncia, que finalmente identifica o que o observador ûˋ.
Na sua interpretaûÏûÈo O observador ûˋ a consciûˆncia .
Isto aproxima-nos mais da concepûÏûÈo de " realidade independente"^ ou " realidade revelada"^ introduzida pelo fûÙsico Bernard_d_Espagnat para o entendimento filosû°fico da mecûÂnica quûÂntica.
bernard_d_espagnat_physique_quantique_et_rûˋalitûˋ_la_rûˋalitûˋ_c_est_quoi ;Recuperado de \" https://wwww.
youtube.
com/watch?v=Jd8FiWJ5v8M; Isto tambûˋm nos aproxima da concepûÏûÈo Vûˋdica na ûndia antiga da realidade material descrita como "Maya"^ ou da ilusûÈo dos sentidos.
Este Maya sendo feito pelas infinitas inter-relaûÏûçes entre trûˆs elementos : richi, chandas e devatta que sûÈo o sujeito, o objecto e a sua relaûÏûÈo, o conhecimento (espiritual: da mente) ou a percepûÏûÈo (material: do material).
O observador da consciûˆncia e a realidade quûÂntica nûÈo material criam uma realidade material fenomenolû°gica.
A este respeito, o filme Matrix ûˋ uma alegoria da realidade, a û¤nica diferenûÏa, e ûˋ importante, ûˋ que nûÈo sûÈo as mûÀquinas que criam a realidade ilusû°ria, mas a prû°pria consciûˆncia.
Assim, a consciûˆncia pode ser definida como a relaûÏûÈo do sujeito com o objecto atravûˋs da percepûÏûÈo ou do conhecimento.
As seguintes trûÙades sûÈo equivalentes:
samhita_tab_pt
veda filosofia fûÙsica quûÂntica
rishi assunto observador connoisseur observador
devatta percepûÏûÈo (relaûÏûÈo sujeito/objecto) observaûÏûÈo conhecimento observûÀvel chandas objecto observado conhecido resultado da mediûÏûÈo: valor prû°prio do observûÀvel
Esta posiûÏûÈo diz que entre duas mediûÏûçes nûÈo hûÀ nenhum objecto e que o û¤nico objecto que existe ûˋ "o objecto observado"^.
O termo clûÀssico corresponde ao que a humanidade como um todo percebe da mesma forma. Mas esta posiûÏûÈo entra em conflito com
realidade quûÂntica, que ûˋ, portanto, entendida como totalmente paradoxal.
e que, como tal, deve ser legitimamente a referûˆncia absoluta.
O problema central ou pivotal entre a realidade quûÂntica e a clûÀssica ûˋ o da decoerûˆncia.
Decoherence ûˋ a transiûÏûÈo da operaûÏûÈo quûÂntica para a clûÀssica.
Ou seja, quando o sistema foi descodificado, ûˋ classicamente descritûÙvel porque o aspecto quûÂntico desapareceu..
Quando se estuda a mecûÂnica quûÂntica, mostra-se que ela se reduz û s leis da mecûÂnica clûÀssica quando considerada em escalas macroscû°picas.
Decoherence ûˋ o facto de passar da descriûÏûÈo do sistema fûÙsico por uma û¤nica funûÏûÈo de onda para a descriûÏûÈo de um conjunto separado de corpû¤sculos.
Quando a funûÏûÈo de onda de um conjunto de partûÙculas "decoheres"^ no colapso da mediûÏûÈo, o aspecto de onda da mecûÂnica quûÂntica desaparece e apenas o aspecto de partûÙcula permanece.
A teoria fûÙsica que trata da descriûÏûÈo de um grande conjunto de corpû¤sculos ûˋ a termodinûÂmica estatûÙstica, que tem os seus fundamentos na teoria quûÂntica atravûˋs da estatûÙstica quûÂntica de BûÑse-Einstein e Fermi-Dirac.
Esta teoria, que foi desenvolvida no sûˋculo XX, permite recuperar os resultados da termodinûÂmica macroscû°pica do sûˋculo XIX a partir de consideraûÏûçes microscû°picas.
A termodinûÂmica opera no mundo clûÀssico da decoherûˆncia enquanto a mecûÂnica quûÂntica opera no mundo quûÂntico da coerûˆncia das ondas.
Decoherence ûˋ a transiûÏûÈo do mundo quûÂntico para o mundo clûÀssico.
Dominar a decoerûˆncia ûˋ o desafio de produzir o computador quûÂntico.
Alain Aspect na sua palestra Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_rûˋvolution_quantique admite a este respeito (a 1H23mn) que se o computador quûÂntico pode um dia tornar-se uma realidade, nûÈo vûˆ razûÈo para que o cûˋrebro nûÈo possa ser um.
Assim, as duas realidades nûÈo-fûÙsicas: a consciûˆncia e a funûÏûÈo da onda podem ser na realidade uma e a mesma.
O Estado . Phi
de qualquer sistema quûÂntico nûÈo relativista ûˋ uma soluûÏûÈo da equaûÏûÈo de SchrûÑdinger, dependente do tempo: 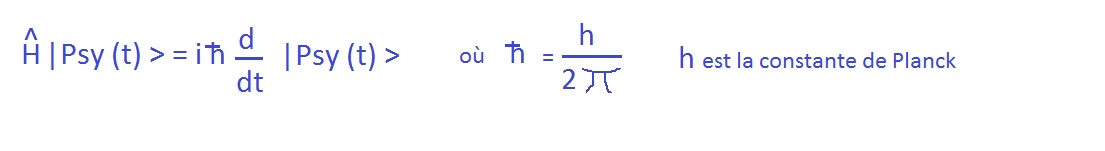 O sexto postulado ûˋ o. ûˋquation de SchrûÑdinger
.
O sexto postulado ûˋ o. ûˋquation de SchrûÑdinger
.
Esta ûˋ a equaûÏûÈo dinûÂmica da mecûÂnica quûÂntica.
Significa simplesmente que ûˋ o operador 'energia total' do sistema, ou Hamiltoniano, notado "H"^, que ûˋ responsûÀvel pela evoluûÏûÈo do sistema no tempo.
(Tradicionalmente na mecûÂnica quûÂntica, os operadores recebem um chapûˋu para os distinguir de outros objectos matemûÀticos, tais como os valores prû°prios.ûˋquation de SchrûÑdinger) A forma da equaûÏûÈo mostra que ao aplicar o operador hamiltoniano û funûÏûÈo de onda do sistema, obtemos a sua derivada em relaûÏûÈo ao tempo, ou seja, como varia no tempo.
(para uma variaûÏûÈo delta t do tempo por isso "dt"^ temos uma variaûÏûÈo "^d | Psy(t) >" da funûÏûÈo de onda).
Assim, se aplicarmos o operador Hamiltoniano (ûˋnergie) para a funûÏûÈo de onda obtemos a sua evoluûÏûÈo no tempo.
û evidente que ûˋ a energia que faz as coisas acontecer.
A energia e o tempo estûÈo intrinsecamente ligados.
Diz-se que formam um par de variûÀveis conjugadas.
Esta equaûÏûÈo sû° ûˋ vûÀlida no quadro nûÈo-relativista.
No quadro relativista, a equaûÏûÈo vûÀlida ûˋ a equaûÏûÈo de Klein-Gordon.
cf Olivier_castera_free_Equation_de_Schrodinger_pdf O operador Hamiltoniano H ûˋ composto por todas as energias que intervûˆm no sistema.
Estas energias sûÈo de dois tipos: energia cinûˋtica e energia potencial.
A energia cinûˋtica ûˋ a energia contida numa massa em movimento.
Uma pedra atirada por uma janela quebra-a em virtude da energia cinûˋtica que adquiriu quando lhe foi dada uma certa velocidade.
Se houver vûÀrias placas de vidro sucessivas, quanto maior for a velocidade da pedra, mais placas de vidro passarûÀ por ela.
A energia potencial ûˋ devida aos campos de forûÏa que se aplicam ao sistema.
Se um calhau cair sobre uma janela no chûÈo, ganharûÀ velocidade devido û energia potencial gravitacional que possui devido û sua distûÂncia da terra..
Quanto mais o tempo passa, mais a energia potencial se transforma em energia cinûˋtica e quando o calhau chega ao chûÈo, quebra a janela em virtude da energia cinûˋtica que adquiriu em detrimento da sua energia potencial, que perdeu.
Se o empurrar para um poûÏo, continuarûÀ o mesmo processo atûˋ que a sua energia potencial se esgote totalmente, se isso for possûÙvel.
Se considerarmos o movimento de um pûˆndulo (um calhau preso a um suporte por um cordel) este û¤ltimo oscila, ou seja, a partir da posiûÏûÈo inicial (a um determinado ûÂngulo a partir da vertical) onde o calhau ûˋ largado, o calhau acelerarûÀ atûˋ a corda estar vertical, depois abrandarûÀ atûˋ parar do outro lado numa posiûÏûÈo simûˋtrica û posiûÏûÈo de partida e vertical.
O pûˆndulo transforma a sua energia potencial em energia cinûˋtica e depois a sua energia cinûˋtica em energia potencial, e isto ciclicamente.
Se o sistema nûÈo for sujeito a qualquer outra forûÏa, o movimento nûÈo pûÀra.
Na prûÀtica hûÀ sempre forûÏas friccionais que dissipam a energia em calor atûˋ û sua exaustûÈo.
Mas este û¤ltimo ponto sû° ûˋ verdadeiro na mecûÂnica clûÀssica porque na mecûÂnica quûÂntica nûÈo hûÀ fricûÏûÈo ! Outro sistema onde existe uma transformaûÏûÈo cûÙclica entre energia potencial e cinûˋtica ûˋ o movimento de um satûˋlite em torno de um planeta, por exemplo a Lua e a Terra.
A soluûÏûÈo da mecûÂnica clûÀssica neste caso mostra que a trajectû°ria do satûˋlite ûˋ uma elipse, ou seja, hûÀ um momento em que a lua estûÀ mais afastada da terra (energia potencial mûÀxima e energia cinûˋtica mûÙnima, apogeu) e outra altura em que a lua estûÀ mais prû°xima da terra (energia potencial mûÙnima e energia cinûˋtica mûÀxima, perigeu).
Os sistemas que acabamos de descrever sûÈo sistemas clûÀssicos mas tûˆm a sua correspondûˆncia no domûÙnio quûÂntico.
Por exemplo, o modelo de pûˆndulo em mecûÂnica quûÂntica ûˋ chamado oscilador harmû°nico e o modelo de satûˋlite corresponde ao modelo de ûÀtomo de hidrogûˋnio: um satûˋlite electrû°nico de um protûÈo.
Na mecûÂnica quûÂntica, a energia cinûˋtica ûˋ um operador que envolve massa, e a energia potencial ûˋ, evidentemente, tambûˋm representada por um operador cuja forma dependerûÀ das energias envolvidas: potencial elûˋctrico, magnûˋtico, ...
A forma como a massa estûÀ envolvida na equaûÏûÈo de Shroedinger, provûˋm do trabalho anterior de Louis de Broglie que estabeleceu a dualidade onda-corpû¤sculo: a cada partûÙcula de matûˋria, podemos associar uma onda cuja frequûˆncia ûˋ proporcional û massa.
Isto ûˋ baseado nas duas fû°rmulas de energia: E = m côý que ûˋ a fû°rmula energûˋtica da relatividade especial de Einstein : a massa ûˋ equivalente û energia E = h * nu que ûˋ a relaûÏûÈo Planck-Einstein que explica o efeito fotoelûˋctrico : a energia ûˋ proporcional û frequûˆncia.
Assim, vemos que na equaûÏûÈo de Shroedinger estûÀ integrado um resultado da relatividade especial de Einstein.
û importante compreender que as energias envolvidas exercem uma restriûÏûÈo sobre o sistema, ou seja, sobre a funûÏûÈo de onda.
Ao lidar com sistemas oscilatû°rios, tais como o oscilador harmû°nico (pendule) ou o ûÀtomo de hidrogûˋnio (satûˋlites)O efeito da restriûÏûÈo energûˋtica ûˋ a localizaûÏûÈo da funûÏûÈo da onda numa regiûÈo do espaûÏo.
Por exemplo, um sistema clûÀssico sujeito a nenhuma forûÏa (um meteoro perdido no espaûÏo interestelar onde as forûÏas gravitacionais das estrelas podem ser negligenciadas) irûÀ mover-se em linha recta indefinidamente.
O equivalente quûÂntico ûˋ uma onda plana que se propaga indefinidamente, tal como um fû°ton que nûÈo estûÀ sujeito a qualquer forûÏa (os fotûçes sûÈo partûÙculas sem massa ou carga elûˋctrica de qualquer tipo e, portanto, nûÈo estûÈo sujeitos a qualquer forûÏa ou energia).
Quando a funûÏûÈo de onda tem uma soluûÏûÈo cûÙclica (funûÏûÈo de onda localizada) o tempo jûÀ nûÈo tem o efeito de afastar as partes do sistema umas das outras indefinidamente.
O electrûÈo permanecerûÀ localizado perto do seu nû¤cleo, que ûˋ o protûÈo no caso do ûÀtomo de hidrogûˋnio.
Ao mesmo tempo, se a onda quûÂntica se propagar ciclicamente numa regiûÈo finita, sobrepûçe-se a si mesma e, portanto, interfere consigo mesma de forma construtiva ou destrutiva.
Ao resolver a equaûÏûÈo Shroedinger de tais sistemas, vûˆ-se que o tempo jûÀ nûÈo intervûˋm sob a forma da funûÏûÈo de onda e que ûˋ apenas espaûÏo (a posiûÏûÈo) que determina a forma da onda.
Este ûˋ o caso de ondes_stationnaires_pt que jûÀ foi mencionado.
Ou seja, os lugares onde a interferûˆncia ûˋ construtiva sûÈo sempre os mesmos que os lugares onde ûˋ destrutiva.
A onda de pûˋ ûˋ um conceito poderoso que nos permite compreender como um fenû°meno estûÀtico pode surgir de um fenû°meno dinûÂmico.
Este ûˋ um dos elementos que permite a integraûÏûÈo da visûÈo quûÂntica: toda a estabilidade da matûˋria que experimentamos provûˋm de um emaranhado de ondas em constante movimento, mas cuja interferûˆncia resultante ûˋ estûÀvel.
Para o ûÀtomo, isto dûÀ û°rbitas bem definidas cujas formas sûÈo fornecidas pelas funûÏûçes da soluûÏûÈo da equaûÏûÈo de Shroedinger, as orbitais atû°micas: as nuvens sûÈo as nuvens de probabilidades de presenûÏa do electrûÈo.
Quanto mais densa for a nuvem, maior a probabilidade de o electrûÈo estar presente.
 RepresentaûÏûÈo da amplitude da probabilidade de ondas em pûˋ (harmû°nicas) do oscilador harmû°nico.
RepresentaûÏûÈo da amplitude da probabilidade de ondas em pûˋ (harmû°nicas) do oscilador harmû°nico.
Note-se a semelhanûÏa com os estados de vibraûÏûÈo (Nû°s de vibraûÏûÈo e barrigas) de uma corda vibratû°ria.
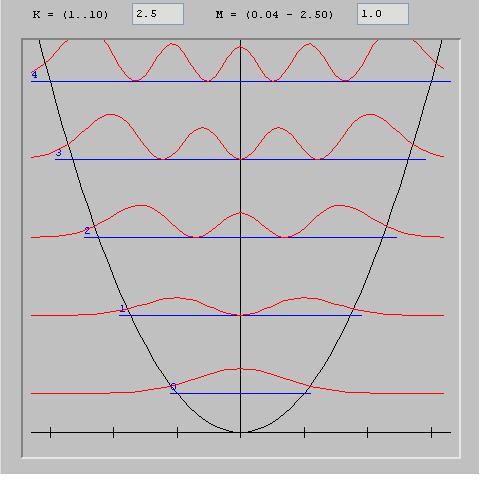
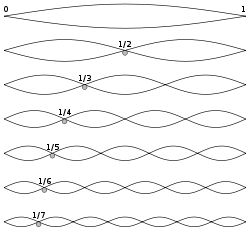 Notamos que no caso quûÂntico (esquerda) a amplitude de probabilidade das funûÏûçes das ondas (em vermelho) diminui progressivamente û medida que se afasta do centro, ou seja, em regiûçes onde o potencial se torna mais forte (curva parabû°lica em preto) mas nunca ûˋ completamente zero.
Notamos que no caso quûÂntico (esquerda) a amplitude de probabilidade das funûÏûçes das ondas (em vermelho) diminui progressivamente û medida que se afasta do centro, ou seja, em regiûçes onde o potencial se torna mais forte (curva parabû°lica em preto) mas nunca ûˋ completamente zero.
Assim, hûÀ uma hipû°tese de a partûÙcula ser encontrada numa regiûÈo remota onde a energia potencial ûˋ superior û energia cinûˋtica, enquanto que classicamente ficaria presa na regiûÈo onde o potencial ûˋ inferior û sua energia cinûˋtica..
Este facto ûˋ a razûÈo para aeffet_tunnel que permite a uma partûÙcula quûÂntica atravessar uma barreira potencial cuja energia ûˋ superior û energia da partûÙcula porque a funûÏûÈo da onda nûÈo ûˋ zero no outro lado da barreira permitindo que a partûÙcula seja aûÙ observada.
Isto ûˋ uma consequûˆncia do aspecto nûÈo-local da funûÏûÈo de onda.
Esta ûˋ a restriûÏûÈo que a energia impûçe û funûÏûÈo de onda para permanecer localizada e assim interferir em si mesma para produzir ondas em pûˋ associadas a valores particulares de energia (Valores quantificados, portanto) que ûˋ a origem do conceito de "quantificaûÏûÈo"^.
Finalmente, ûˋ necessûÀrio falar sobre o que estûÀ na origem da teoria quûÂntica: o constante_de_Planck que aparece na equaûÏûÈo de Shroedinger.
Esta constante foi introduzida pelo fûÙsico Max_Planck para explicar o valor da radiaûÏûÈo tûˋrmica da matûˋria em funûÏûÈo da temperatura.
A lei observada que esta radiaûÏûÈo segue obriga-nos a considerar que a energia tûˋrmica nûÈo ûˋ emitida continuamente, mas sim em pacotes ou "quanta"^..
Esta ûˋ a primeira prova da natureza quûÂntica da matûˋria.
Na fûÙsica, a acûÏûÈo ûˋ definida como o produto da energia e do tempo.
û bastante intuitivo: quando uma energia actua durante um certo tempo gera uma certa acûÏûÈo cujo valor ûˋ proporcional ao da energia e ao perûÙodo de tempo durante o qual actua.
A constante de Planck representa a menor acûÏûÈo possûÙvel no mundo fûÙsico.
û uma constante universal da fûÙsica que caracteriza a natureza quûÂntica da realidade.
O valor desta constante ûˋ extremamente pequeno: 6,62607004 û 10-34 m2 kg / s mas no entanto nûÈo ûˋ zero.
que sûÈo chamadas unidades Planck.
Assim, o mundo fûÙsico descrito pela mecûÂnica quûÂntica tem um limite no infinitamente pequeno para alûˋm do qual jûÀ nûÈo podemos falar em termos de fûÙsica, ûˋ finalmente um limite do mundo fûÙsico.
Se existe uma borda, um limite, ûˋ uma restriûÏûÈo quûÂntica natural para a funûÏûÈo de onda e, portanto, para a quantizaûÏûÈo (que ûˋ em si mesma, como vimos, uma forûÏa).
A constante de Planck define a pixelizaûÏûÈo do Universo.
A origem mais fundamental da quantificaûÏûÈo pode tambûˋm ser encontrada no funcionamento da consciûˆncia, que por natureza nûÈo ûˋ contûÙnua.
De facto, se considerarmos a observaûÏûÈo por um sujeito de um objecto que ûˋ um ponto de vista na consciûˆncia, isto sû° ûˋ possûÙvel atravûˋs da discriminaûÏûÈo da consciûˆncia de diferentes pontos de vista possûÙveis.
Para que sejam identificados, os pontos de vista devem ser distintos, caso contrûÀrio todos os pontos de vista se fundiriam e nûÈo haveria uma observaûÏûÈo real.
DiscriminaûÏûÈo ûˋ a qualidade do intelecto que ûˋ, neste sentido, uma propriedade fundamental da consciûˆncia.
Encontramos assim os elementos presentes nos postulados quûÂnticos de mediûÏûÈo.
"
1.5.1.AnûÀlise do aforismo
poema correspondûˆncia quûÂntica link para os postulados
O que ûˋ a funûÏûÈo de onda ou vector de estado ou "ket" (de parûˆntesis , gancho em francûˆs) . Premier postulat
possûÙvel a estrutura probabilûÙstica da funûÏûÈo da onda, as diferentes possibilidades eigenstatos do ket . Troisiû´me postulat ûˋ realizado a dinûÂmica do operador Hamiltoniano a energia total do sistema responsûÀvel pela evoluûÏûÈo. . Deuxiû´me postulat sob o olhar da consciûˆncia os postulados de mediûÏûÈo, ou seja, a intervenûÏûÈo necessûÀria do observador . Quatriû´me postulat sû° se consegue o que ûˋ possûÙvel apenas os valores prû°prios do observûÀvel podem ser obtidos e o estado do sistema ûˋ entûÈo o estado eigenstate correspondente. . Cinquiû´me postulat O que ûˋ possûÙvel ûˋ conseguido a equaûÏûÈo de SchrûÑdinger, a equaûÏûÈo da dinûÂmica quûÂntica. . Sixiû´me postulat
A grande dificuldade que os cientistas tûˆm em aceitar a mensagem da teoria quûÂntica explica por que razûÈo tûÈo poucas pessoas podem aceder a ela.
Aqui encontrarûÀ um resumo desta situaûÏûÈo, analisado por Jean Staune e relatado por Bruno Lussato: bruno_lussato_les_plus_grandes_dûˋsinformations_de_l_histoire_des_sciences
(blog onde, em 2009, deixei um relato da conferûˆncia que Alain Aspect deu em 1982, em Toulouse, quando estava em digressûÈo pelas universidades francesas para apresentar os resultados do seu trabalho.bruno lussato a maior desinformaûÏûÈo da histû°ria da ciûˆncia nweb) Este texto poderia ter sido escrito e provavelmente muito melhor por um grande nû¤mero de pessoas conhecedoras que fazem parte do estabelecimento cientûÙfico "^ mas a sua relutûÂncia em fazûˆ-lo levou-me, por um lado, a ser capaz de reservar o nome de domûÙnio quantum.
org que, curiosamente, estava disponûÙvel e, por outro lado, para passar dezenas de horas a elaborar este texto que, provavelmente, ainda terûÀ de ser melhorado...