量子力学のポスチュレート
version available in : en it ru zh es de nl pt fr
date of creation : 20240129- date of update : 20221007- generation date : 20241110_231431
本稿では、その詳細を紹介する。 postulats_de_la_mécanique_quantique簡単な数学的、幾何学的な考察と日常生活から得た類推から.
物理学では、数学的な対象に関する概念を発展させ、その動作法則によって物理世界を表現する理論を確立している.
古典力学やニュートンの理論は、人間の知覚に敏感なスケールで物質の働きを表現することができる理論で、私たちはそれをマクロと呼んでいます.
宇宙論的スケールでは、この理論はアインシュタインの相対論的理論によって一般化される.
一般相対性理論は、重力の力を最も完全に扱う理論である.
量子力学は、物質の働きをミクロのレベルで表現できる理論ですが、ミクロとマクロの境界がスケールで明確に定義されていないため、マクロのスケールで量子の振る舞いがあるように laserまたは cables_électriques_supraconducteurs 量子論は、一般相対性理論のような特定の自然界の力を扱うものではなく、むしろ言語である.
量子オブジェクトの言語.
したがって、この言語を様々な力やシステムに適用することで、それらを定量化することができます.
一連の量子コンセプトは、以下を中心に展開されます。 ろくがくしゅうげんていぎ.NAVER超電導電力ケーブル この6つのポスチュレーションを提示し、その意味をわかりやすく整理してみます。.
1.1.第一仮定
.
コーエン=タヌージ著「量子力学第1巻」で定義されている第1ポスチュートの表現"は次の通りです。 :
一定の時間tにおいて、物理システムの状態は、以下のデータによって定義される。
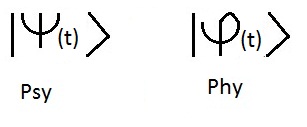
ケットや波動関数、状態ベクトルを記した |サイ(t)>状態空間"に属する.
ポスチュアI nweb
ギリシャ文字のPsyは波動関数を表すのに使われ、私たちは
フィーの文字も淡々と.

力学の最初の概念は、物理システムの状態の表現に関わるものである.
これは、研究の対象を定義するための自然な方法です.ここでは、単に「システムが存在する」というだけである
であり、その状態が時間依存の関数で表現できること
これは、システムの状態がアプリオリに静的ではなく、動的であるためです.
古典力学では、物理系は物質点"で表されます。.
複雑なシステムは、接続された物質点の集合で表現されることになる
の間に、固体または非固体のオブジェクトを形成します。 (硬軟織り交ぜた接続。:結晶又は気体).
第一ポスチュレートは、ある時間におけるシステムの状態が一意であることを簡単に述べている
でグループ化された可能な状態の集合に属し、その集合は
状態空間と呼ばれる数学.
量子状態がベクトルであるため、単純な集合ではなく、空間について話すことになる
は、空間内の方向を表す数学的なオブジェクトである.
私たちは3次元空間について知っています (最初の2つの寸法の向きに応じて、長さ、幅、高さ、または奥行き)
それは、私たちが生活する物理的な空間です.
量子系が生きている状態の空間は、物理的な空間ではなく、抽象的な空間である。 (ヒルベルト空間)
であり、その次元は、単純な物理系であっても存在する可能な状態の無限大を表すために無限大となる.
日常生活での例で例えてみましょう。
量子系がどのようにモデル化されるかを理解するために.
自分のアパートで静かに座っている人を想像してください。
パンを買いに行かなければならないことに気づき.
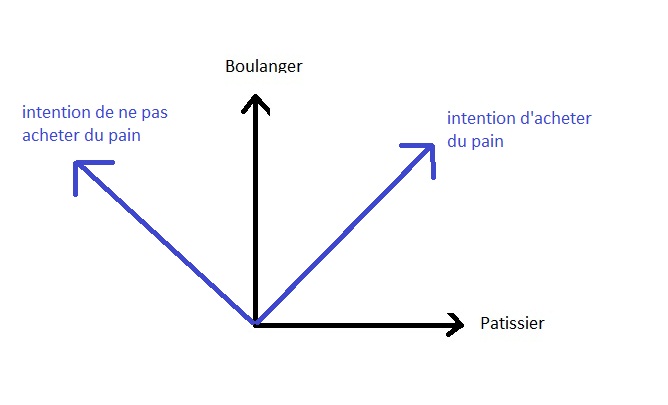
彼女は帰り支度をし、心の中ではまだその場所に迷いがある。 パンを買いに行く.
彼女は、この通りのさらに奥にあるパン屋か、それとも、パティシエもやっている店か、どちらかを選ぶことになる。
を、さらにその下にいる.
階段を下りて出口に向かうと、次の2つの状態があると言えるでしょう。 の2つの選択肢に対応する、彼の頭の中にある可能性のあるものです。 パンを買う.これらのオプションは、量子的な方法で記すことができます:
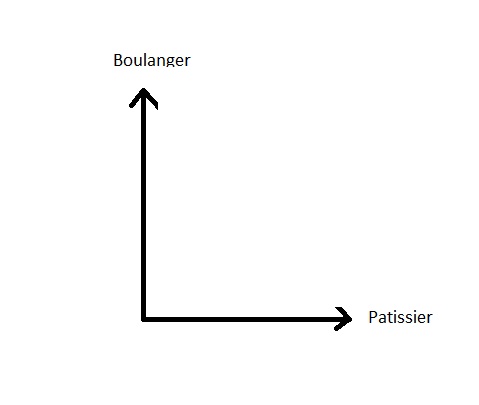
状態1: |パン屋>
ステータス2: |ペストリ>
その人の心の状態は、この2つの可能性の組み合わせです。:
|ステータス> = |パン屋> + |ペストリ>
この2つの状態は完全に相容れないものである:を買ったり、パンを買ったりしている。 パン屋さんでも、お菓子屋さんでも.この2つの可能性は、いずれも 相容れない.幾何学的に これらは直交していると言えるでしょう (直立)と空間における幾何学的表現 (かの国の)であろう:
したがって、私たちは、何の共通点もない2つの非常に異なる方向性を持っています。.
矢印の場合 (ベクトル)パン屋は矢のほうに傾いていた (ベクトル)ペストリ
ということになります。
ペストリ さんが買いに行くのと少し連動しています。
のパティスリーでは、そうではなく、2つの
非対応選択肢:直交:しゅのうぶっつり.
一方、システムの状態、すなわち心の状態については
の2つの状態のいわゆる線形結合である。.
状態が混在していることを言います.本当の混合状態は
見るに見かねる:どうかな
パンを買うところではない.
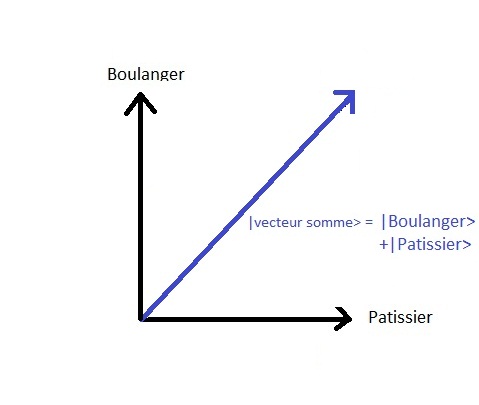
この2つの可能性の線形結合は、次のように対応します。
を、観測可能な状態を表す2つのベクトルの和に変換する。.
2つのベクトルの和は以下のように実現されます。 :そうです
第1ベクトルの終端と第2ベクトルの終端から
ひめはじめ
秒の.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
状態空間は、ベクトル空間、すなわち方向の空間と言われた。 これは、幾何学的な表現では、ベクトルを変えずに移動できることを意味する の性質上、同じベクトルであることに変わりはありません。:同じ方向を向いている.また、簡略化するために のみであることを示すために、すべてのベクトルが同じ点から始まるように表現しています。 余談.に対して、これはベクトル空間と呼ばれます。 を、数学ではアフィン空間と呼ばれる点の空間に変換する。. (が表示されている画面 この文章を読んでいるあなたは、画素がその空間の点を表すアフィン空間の一例です。.状態和集合ベクトルimg)
幾何学的な表現は、ベクトル空間であるため、当然、点の空間で行われます
は純粋に抽象的なものであり、我々が知覚する空間においてのみ、点で表現することができる (役職)別.
しかし、これは状態空間には存在せず、あるベクトルの異なる表現がすべて
表現空間内の位置は,ベクトル空間内の1つのベクトルに対応する.
したがって、状態は次のように表すことができる。 :
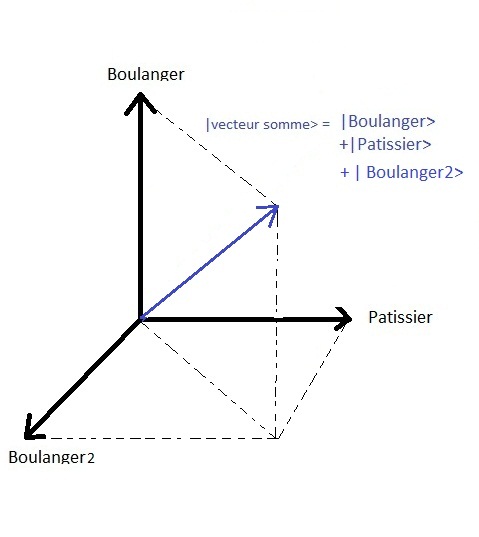
ここで、状態空間の次元は、2.もし第3の選択肢があったなら
まちまちのパン屋さんと |ベーカー2 >とすれば、状態空間は3次元となる。.
物理学では、2状態系は同じようにモデル化することができる.
これは、イオン化した水素分子の場合です.水素分子
は、2個の水素原子核、すなわち2個の陽子から構成されている
で、イオン化しているということは、そこから電子が取り除かれたことを意味します
持ちつ持たれつ.例えば
単純であるが故に :1個の電子に"。.
電子の位置状態には、次の2つが考えられる。 : - 電子が原子核の中心にあるかどうか 1 - 電子が原子核の中心にあるかどうか 2
幾何学的な表現は:
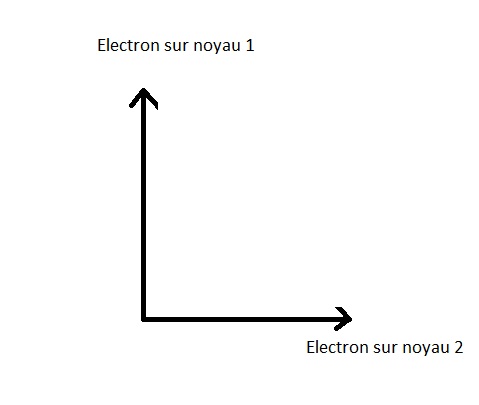
電子を見つけることができないことは明らかである (見付かるというか :みとれる)をコア1とコア2で同時に使用する場合、これらの状態は直交しています。.
ポスチュートの表現では、状態ベクトルを指定するために同義語が使われ、これを無関心に呼ぶと
状態ベクトル、波動関数、ケット.これらの異なる名称は、状態ベクトルの異なる数学的側面に対応している.
波動関数の側面は第2ポスチュレートの説明で、^ケット^の側面は第3ポスチュレートの説明で見ることになる。.
要約すると、量子状態は与えられたベクトル (方向)ベクトル空間において (指示事項),
このベクトルを状態ベクトルと呼びます。.
古典力学では、状態は物理的性質によって定義される"物質点"によって表されます。 いんしん.
ここで重要なのは、量子力学では、系の状態は全く独立であることだ。
システムの物理的特性.状態は抽象的に定義され、非物理的と言えるかもしれません"。.
これは、"状態ベクトル表現基底"の概念を通じて、以下のポスチュレートを提示する際に詳述される。.
しかし、第一仮定では、状態ベクトルは時間のみに依存し、位置には依存しないことに注意する必要があります
という空間である。.これは、波動関数が非局所的であることを意味します.
相対性理論では、時間と空間は連続体であるとされており、したがって、もし
量子力学では、少なくとも特殊相対性理論を考慮すると、状態ベクトルは
じだい.この理論は、量子電気力学または電磁場の量子理論である.
特殊相対性理論は、アインシュタインが生み出したという事実によって、電磁気学と非常に密接な関係がある。
マクスウェルの電磁気理論が提起したパラドックスを取り除くために.
量子力学の概念は、純粋な想像力によって生み出されたものではない.むしろ、実験の火の中で鍛え上げられたものです。
これらの概念を適切に表現する必要があったミクロフィジックスの.
抽象的ではあるが、量子状態は実在する.
この量子状態の現実は、たとえ避けられないものであっても、しばしば最も認めがたいものとして残っているのです.
最も具体的なものである物質の働きは、全く抽象的なものによって支配されているのです.
とはいえ、この量子概念が極めて強固なものである以上、この難題を回避することは不可能である.
認知の状況は、電磁波の発見とやや似ている.これらの波は、最初に理論的に
電場と磁場を記述するマクスウェルの方程式を組み合わせて発見された.
これらの組み合わせにより、速度が一定の波の伝搬方程式が得られた.それは抽象的な概念であった
と新しいが、電場や磁場が波を発生させることは実験によって明らかにされている。
を制御・利用できるようになり、無線通信が可能になった。.
この速度が、測定された光速であることを見てきました.
同じように、波動関数という非常に抽象的な概念が、非常に具体的になったのはintrication_quantique という技術領域を生み出しました。 cryptographie_quantique
Postulat_II
観測可能な物理量「a」は、状態空間に作用する演算子「A」によって記述されます。;この演算子は観測可能.
" 古典力学では、物質点の性質、速度、位置がその状態を決定することを見てきた.
例えば、テニスコート上のボールの速度や位置、太陽系内の惑星の位置など.
巨視的な物体の位置と速度は各瞬間に決定され、これによってシステムの状態が完全に定義される.
空間におけるテニスボールの進化は、ボールが動いているのか、アウトなのか、ネットに引っかかった後地面に動かないのか、それぞれの瞬間にゲームの状態を定義します。.
そして、試合とその結果を決定づけるのは、その州の歴史である.
一方、量子力学では、先ほどの電子のような粒子に還元された系の一般的な状態は、もはや特定の位置や速度ではなく、すべての可能な位置や速度の混合物と関連づけられます.
さらに、古典力学のようにシステムのすべての特性を同時に観測することはできないので.
システムが位置の状態にある場合、エネルギーの状態にはなく、その逆も同様です.
パンの例では、パンを買った場所を示すパン屋と菓子屋という位置的な状態があるが、これから見るように、これはエネルギー状態ではない。.
水素分子の例と同じように、電子が1番原子核や2番原子核に位置していることは位置状態を表していますが、それ自体は分子のエネルギー状態ではないのです.
量子系では、異なる性質が同じ状態空間を共有しているが、異なる性質に対応する状態は、必ずしも空間内の同じ方向で表現されるとは限らない.
つまり、空間が2次元であれば、2つの位置状態と2つのエネルギー状態が存在し、エネルギー状態は位置状態と同じ方向を持たないということだ.
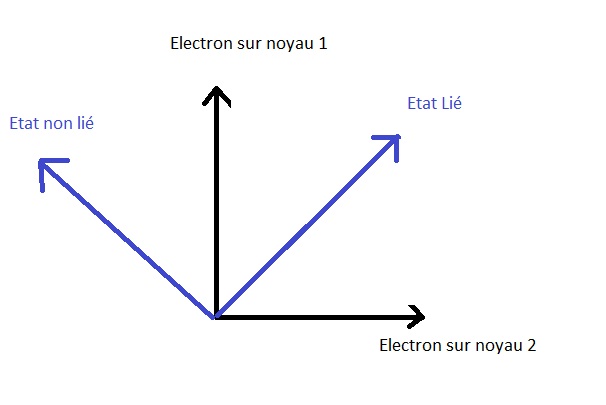
水素分子の場合 (でんきしき)は、可能なエネルギー状態は:
|ステータス:エネルジー> = |かんれんじょうたい> |未解決状態>
水素分子の動的またはエネルギー的な"表現で.
システムの一般的な状態は、その特性から完全に独立しているので、パンについては、次のように書くことができます。:
|ステータス> = |決意> |ききゃく> = |パン屋> |パン屋>
水素分子がElを呼び出す場合 (かんれんじょうたい)とエンル (未解決状態)はエネルギー状態、P1 と P2 は位置状態であり、以下のようになります。:
|ステータス> = |があります。 > |エンエル > = |P1 > |P2 >
状態が観測可能な性質とは無関係であり、それに関係なく表現できることは、量子力学の基本的な特徴である.
この特性は数学的演算子で表され、これを量子状態に適用すると、その特性に関する可能な状態が決定される.
数学における演算子とは、広い意味で値を進化させるものである.
例えば、足し算の演算子 "3 " を "2 " に適用すると、^3 2^ となります。=演算子 "3 " を適用して、^2^ から "5^ へと値を変更しました。 (さんだんかまえ) 量子力学では、演算子が状態を進化させる.
このポスチュレートは、演算子"が状態空間上で作用することを意味します。.
Pを位置演算子、Eをエネルギー演算子とすると (現実には、エネルギー演算子はHと表記されます。 hamiltonien_jaは、ハミルトンが一般力学で定義した、系に作用するすべてのエネルギーの総和である全エネルギー関数である).
第2仮定によれば、これらの演算子は対応する性質を表します。 (せいいっぱい)システムの.
適用することにより (軌道修正)であり、水素分子の状態に関する位置演算子として:
P | > = |P1 >またはP |地位 > = |P2 >.
状態に対して演算子を適用することは、演算子に対応する性質(ここでは位置)を観測することを意味します。.
エネルギー演算子と同じように.
H |地位 > = |があります。 > またはH |地位 > = |エンエル >.
我々は、オペレータを状態に適用するとき、この状態を、この特定のオペレータに属する状態へと進化させることがわかります。 クリーンな状態"。演算子の.
結果は、システムにとってもオペレータにとっても、あらゆる可能な状態になりうる (被測定物).
国家 結合分子はエネルギー演算子の固有状態であるのに対し コア上の電子1"は演算子の位置の固有値である.
結合状態の水素分子では、電子は2つの水素原子核の間の不確定な位置にある.
エネルギー固有状態は、位置状態の線形結合と言うことができ、次のように表すことができる。:
|があります。 > = |P1 > |P2 >
2つの位置状態を足し合わせると、エネルギー状態になると言えます:電子が2つの原子核に共有されている場合、分子は結合しており、2つの位置状態は建設的に干渉し、^結合^エネルギー状態を形成すると言われています。.
で表現されるのと同じように、バインドされていない状態は |エンエル > = |P1 >- |P2 >
この2つの位置関係は破壊的に干渉し、エネルギー状態 "unbound^ を生成すると言われています。.
再びパンに例えるなら、その人の心の状態は、パン屋にパンを買いに行くか、パティシエにパンを買いに行くかの迷いであると同時に、パンを買いに行くか、パンを買わないかの迷いでもあるのです.
パンを買いに行くという決意があるといえます。 interférence_jaパンを買いに行く可能性があるのに対して、放棄は interférence_ja同じ可能性のある状態を破壊する.
システムに起こりうる、状態空間に含まれるすべての可能性を考慮する。.
幾何学的にこれは次のように表すことができる。:
 観測可能なエネルギー状態であることがわかります。 (分子の結合状態または非結合状態)は、互いに相容れない可能性のあるエネルギーオプションに対応するため、直交でもある.
観測可能なエネルギー状態であることがわかります。 (分子の結合状態または非結合状態)は、互いに相容れない可能性のあるエネルギーオプションに対応するため、直交でもある.
システムの状態 (状態ベクトル)は、それ自体、エネルギーや位置に関する状態空間での表現とは無関係である。.
演算子に関連する固有状態は、状態ベクトルを表現するための基底であると言われています (青色または黒色ベース) このように、状態ベクトルに対して、位置演算子の表現基底とエネルギー演算子の異なる表現基底があります.
があります。 principe_d_incertitude_de_Heisenberg量子力学の定理から直接導かれる.
一般に、2つの観測値の固有状態は同じベクトルでは表現されず、例えばエネルギー状態は線形結合で表現されることを見てきた (重ね合わせ)位置づけの.
この場合、系の位置の性質とエネルギーの性質の固有状態は両立しないので、同じ測定で両方を観測することは不可能であることは明らかである.
数学的には、演算子は切り替わらないと言います.
つまり、2つの演算子を異なる順序で連続的にシステムに適用すると、最終的な状態は異なるものになるのです.
実際には、量子実験では多数の粒子が観測され、エネルギー値の精度が高いほど位置の精度が低くなり、その逆もあるという大局的な統計結果が得られます。.
状態ベクトルと波動関数の違いは、状態ベクトルは物理空間に依存しないが、波動関数は物理空間を伝播するため、依存しないことである.
量子力学では、波動関数は状態ベクトルの物理空間への射影であると言われている.
下の画像では、波の様相を表現しています (波動関数)りょうしじょうたいの
足し算や引き算によって、波がどのように破壊的または建設的に干渉するかを視覚化する。.
波の基本的な働きは、量子波であろうと、波動であろうと同じです。
電磁波、または水面上の波 (ヴァイグレッツ).
波には必ず谷とピークの振動がある (波の)平均値付近 (水の平らな面).
プラスαを積み重ねる (劣らず)で、プラスとマイナスが引き算されて打ち消されます.
例えば、ある波の谷と別の波の山が重なった場合、両者は打ち消しあい、その結果
重なり合った部分の平水面.
原子や分子の波動状態は、以下のように対応します。 ondes_stationnaires_ja
伝播せず、主に限られた領域に局在する波である
宇宙の、ここでは水素原子核の周りの.

したがって、第2ポスチュレートは、状態を変換するために適用される演算子を紹介します。.
したがって、状態ベクトルは量子的現実の静的な側面を表し、演算子はこの同じ現実の動的な側面を表すと言えるのです.
第3、4、5原理は、量子系を観測する過程そのものを記述しています。.
第3の仮定
.
Postulat_III
測定 :観測可能な値 "物理量Aの測定は、すべての可能な値の中から対応する観測可能なAの固有値のみを与えることができる。.
" 量子系のある性質の観測可能な状態を固有状態^^と呼ぶことを見てきました。 (この観測可能な).
各固有状態"には、関連する"固有値"があり、これは測定の結果である。.
例えば、水素分子の場合、分子が結合している状態と結合していない状態では、分子のエネルギー準位が異なることになる。.
パンの例えで言えば、パンを買ったときに減った財布の中の金額の変化という結果が想像できます.
固有値は数であり、固有状態はこれまで見てきたように、ベクトルである.
これまでのところ、量子状態に関する最も重要な概念として、状態空間の次元と関連するベクトルの方向のみを用いています。.
数学では、ベクトルに関連する自然値はその長さである.
この長さは抽象的です (物理的空間ではないので、メートル単位では測れません。).
このため、長さやスケールを指すより一般的な用語が作られ、スカラ値"と呼ばれるようになりました。.
したがって、スカラーは、ベクトルの長さに関連する数値である.
ベクトルの長さに数値を乗じると、長さが初期値の倍数になるベクトルが得られ、それは異なるスケールで、その新しい値^scalar^となります。.
そこで、エネルギー演算子を用いて、システムのエネルギーを観測しています.
この場合、状態に対してエネルギー演算子を適用すると、2つの可能なエネルギー状態が同時に得られることを見てきました:
に適用されるH |地位 >は、どちらかの状態を与えます。 |があります。 > (リンクへ)エネルギーElに関連する状態は |エンエル > (無関係に)エネルギーエンルに関連する (の固有値である。).
論理演算子 "or^ (または非独占的)は、量子力学では、状態空間において、指摘されたベクトルの加算によって表現される " " 。.
したがって、以下のようになります。:
H |地位 > =があります。 |があります。 > エンエル |エンエル >
ここで、El と Enl は、これまで見てきたように、それぞれ2つの状態のエネルギー値を表しています。.
測定中に1つの値しか取れないことを表現するために、射影と呼ばれるベクトルの性質を利用します.
以下は、グローバルステートプロジェクションのイメージです。 |サイ>エネルギー状態"結合分子"の上で |があります。 >
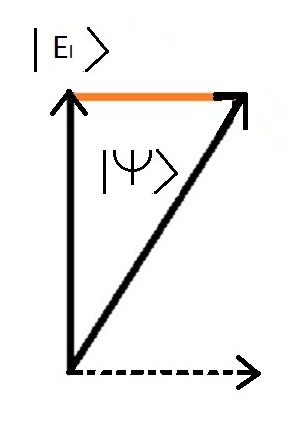 物理的性質を測定する場合、その測定値は一意的な値を与え、この値は固有状態"と呼ばれる系の特定の状態に対応し、得られた値は固有値"と名づけられる。.
物理的性質を測定する場合、その測定値は一意的な値を与え、この値は固有状態"と呼ばれる系の特定の状態に対応し、得られた値は固有値"と名づけられる。.
先ほどの式では、値ではなく、可能性を足しているので、E =El Enl、ベクトルの追加は、値の追加と同じようには動作しません。 (スカラ).
可能性を加えると、エネルギーの総和ではなく、値の総和であるエネルギーの平均値になることは後述します (ici El Enl)を加算した値で割ったもの (アイシーツー).
したがって、平均的なエネルギー値は、E = (エル・エン)/2.
実際には、エネルギーの平均値は、エネルギーの各状態の存在確率にも依存するので、各状態の確率で重み付けした平均値であり、もう少し微妙なところである.
これはまさに第4のポスチュレート(仮定)の主題である.
Postulat_IV
ボーンポストレート :波動関数の確率論的解釈^^正規化された状態^^の系で物理量Aを測定するとき、確率P (An)で、対応する観測量Aの固有値Anを求めると、次のようになります。 |Cn|².
ここで、Cn は固有状態に投影された波動関数の振幅である |ファイ>観測された固有値Anに対応する.
今までは、状態、観測可能な固有値とその関連する固有値についてだけ話してきました。.
状態ベクトルの長さは慣習的に1であり、その理由は、状態ベクトルがシステムの存在を伝えるからである (一義)であり、確率の観点からは、システムの存在の肯定が確実性に対応するものであること.
確率の場合、確実性は1.
1分の1の確率で何かが起こるとき (1÷1=1)われわれは確信犯である.
1未満の確率は、完全な確実性よりも低い確実性である.
例えば、宝くじが1枚だけ当たる確率は、1÷数百万です。.
つまり、最終的に抽選で億単位の賞金を手にするのは、たった一人、あるいはほとんど一人ということになるのです。 ! 量子力学でいうところの抽選は、"当選者の観測です"。.
波動関数の振幅は、状態ベクトルの長さと同じである.
スカラーは単純な数値であることを見てきました.
この呼称は、ベクトルなど、数値で表すと複数の数値を使う必要があるような、より複雑な数値との比較にも登場します.
(この展開に従うと、物理学で非常によく使われる"テンソル"という概念に行き着きます。弾性体のテンソル、時空の曲率のテンソルです...ポスチュレートIV nweb).
_
あるベクトルが別のベクトルに投影されるとき、最初のベクトルから2番目のベクトルに運ばれる長さは、数.
このように、2つのベクトルに数値を関連付ける操作を行ったが、この2つのベクトルの操作の特定の結果は、ベクトルの加算のように第3のベクトルを与えるのではなく、数値 (スカラ).
この演算はスカラー積と呼ばれる: スカラー積は、2つのベクトルから数値を求める演算である.
この数値は、一方のベクトルを他方のベクトルに直交投影した長さである.
英語の^bracket^は、文字"を指します。<" et ">これらの括弧は、数学で伝統的に数量の平均値を表すために使用されています。.
エネルギーの平均値は、例えば次のように表記します。 < E >.
量子状態は "ket^ とも呼ばれることを見てきました。 |ケット > 括弧のもう一方の部分は "bra^ で、これは特定の演算子として注目されています。 <ブラジャー | それは、物理学者である Paul_Dirac平均値をとるという操作において、演算子とベクトルのダイナミズムを出現させるために、この単語を二つに分離したのが、その原点である。.
ブラ"をケ"に当てはめると、次のようになります。 <ブラジャー |ケット >という演算子を適用した結果の数値である。 <ブラジャー|国対して |ケット>或いは、国家の投影 |ブラジャー>国対して |ケット>.
ここでは、ブラとケットの二重の関係になっています.
状態に対して (ウンケット)"|ドッグス >^ le bra sera ^<ドッグス |ケトはベクトル、ブラは演算子で、ケトにブラをかけると数字になる.
一般に、式においてケタの右側にあるものは演算子であり、演算子がある状態に対して行った結果である (ベクトル)は他の国か (ベクトル)測定結果を表す数値または確率のいずれか.
ケットには対応するブラがあり、ケットからブラに移行する操作を隠語的活用と呼び、星印で表記している.
こうして ( |ドッグス > )* = <ドッグス |または ( <ドッグス | )* = |ドッグス > または |ブラジャー> = (ケット>Paul Dirac nweb)* <オペレータ| = (地位>Paul Dirac nweb)* ブラジャーは、したがって、動的な側面です (オペレータ)フカシ (地位)を生じさせるものである。 (測定結果 ).
これは、宇宙の創造主が語るヴェーダの格言になぞらえることができる。: 自分自身を見つめ直し、何度も何度も創作する。.
同じ形は、創世記の最初の創造物語にも見ることができる: 光あれと光あれと光あれと光あれと光あれと光あれ。.
神は光が良いものであることを見た.
<ひかりをかがせる |で、その光は > =とD.
神は光が良いものであることを見た.
<または |light². |樽 > =D.
神は光が良いものであることを見た.
という事実は、D.
神は光が良いものであることを見たというのは、明らかに観察の結果である.
これらすべてを量子アルファベットとシンタックスと呼ぶことができる。.
アルファベットは1文字で構成されています |ドッグス >ということです。 (或いは存在することを肯定している状態) 二重演算 * は、その動的演算値を示す ( |ドッグス > )* = <ドッグス | これらの組み合わせにより、量子文法が生まれる.
例として、演算子の応用として <ドッグス |国対して |ドッグス >与える <サイ|ドッグス >を投影したものでもあります。 |サイ>を自分自身の上に置くので、1.
これは、次のような文章に些細に変換することができます。:Psyは100%参加します。 (100/100=1)をPsyに変更しました。.
<ドッグスL |ドッグス >は、システムの一般的な状態を H2 分子の例の束縛エネルギー状態に投影したもので、ある観測中に束縛状態を得る確率の振幅を表している.
アル = <ドッグスL |ドッグス > 振幅の2乗をとると確率が求まる 状態の確率 |ドッグスL >でございます:Pl =Al² = ( <ドッグスL |ドッグス > )² 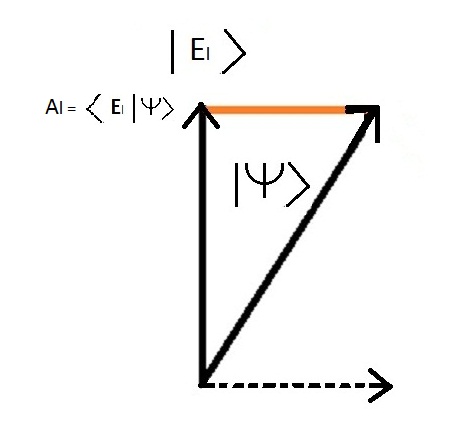
下の画像は、一般的な状態を投影したものです。 |ドッグス >の2つのエネルギー状態について |犬 l >と |犬 nl > (という状態と同じである。 |があります。 >と |エンエル >表記ゆれの違い)
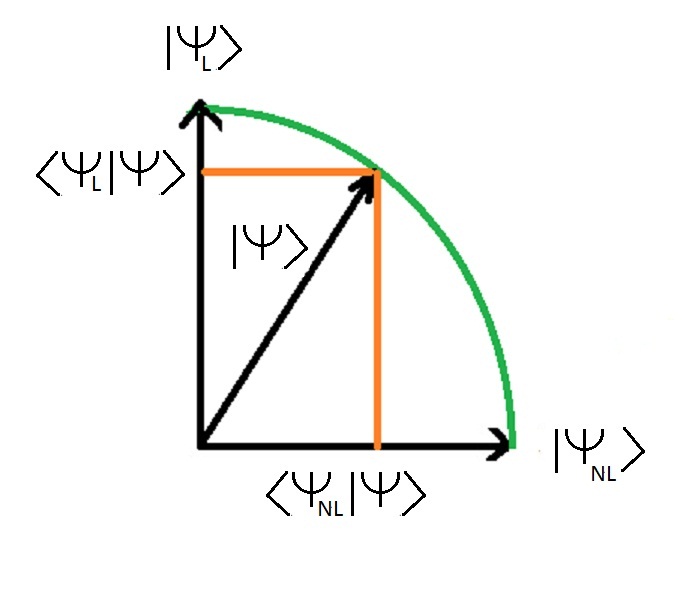 2つの価値 <犬 l |ドッグス >と <犬 nl |ドッグス >は状態の長さ |ドッグス > (というのは、1)じこけんとう |犬 l >と |犬 nl > <犬 l |ドッグス >は、状態の投影 |ドッグス >きれいな状態で |犬 l > <犬 nl |ドッグス >は、状態の投影 |ドッグス >きれいな状態で |犬 nl >
2つの価値 <犬 l |ドッグス >と <犬 nl |ドッグス >は状態の長さ |ドッグス > (というのは、1)じこけんとう |犬 l >と |犬 nl > <犬 l |ドッグス >は、状態の投影 |ドッグス >きれいな状態で |犬 l > <犬 nl |ドッグス >は、状態の投影 |ドッグス >きれいな状態で |犬 nl >
状態を考えたとき、"パンを買う"。 |パン屋>と |パン屋>一方と他方を無差別に、つまり同じ確率で観測できると暗黙のうちに考えていたのです.
これは、等積状態として知られている.
例えば、パン屋がパティシエよりも家に近く、とても寒い場合、この状態の確率は0.5%になる。 |パン屋>の方が強くなる。 |パン屋>.
これは、下の画像でAbがApより大きいことを表しています。.
(Aは確率の振幅).
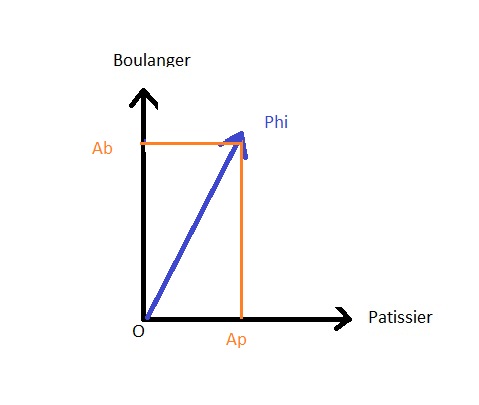 国家の投影 |ファイ>国家元首 |パン屋>は、一般状態からこの状態を得る確率の振幅に対応する値Abを持つ。 |ファイ>同じことが、状態を得る確率の振幅であるApにも当てはまる |パン屋>.
国家の投影 |ファイ>国家元首 |パン屋>は、一般状態からこの状態を得る確率の振幅に対応する値Abを持つ。 |ファイ>同じことが、状態を得る確率の振幅であるApにも当てはまる |パン屋>.
量子固有状態は常に直交しています。つまり、互いに直角であり、したがって . Pythagore
直角三角形に対して.
2辺の長さの2乗の和は、斜辺の長さの2乗に等しい。 この場合、斜辺は状態ベクトルに対応します。 |Φ>と両側から |Φ>2つの固有状態について |パン屋>と |エピシエ>.
このポスチュレートでは、波の振幅の二乗が、確率.
システムの一般的な状態を考えるということは、単純に「ある」と考えることです。:したがって、システムの実際の状態の確率は、常に1に等しい.
このことは、ポスチュレートが言及している、「状態 |Φ>はノルム化され、そのノルムは確率であるため、慣習的に常に1に等しくなります。.
数学的には次のようになります。 <Φ |Φ > =1 = | |Φ> |² (最後の式は,ベクトルのノルムの2乗を表し,ベクトルのノルムはその長さである) この確率は、各固有状態に対応するいくつかの低い確率に分割されるが、システムの固有状態の振幅の二乗和が常に1に等しいという制約があり、これがある確率となる。.
私たちの場合、次のようになります。:
Ab² Ap² =1 システムのすべての可能な状態の確率の和は1に等しくなければならない.
システムの存在は、その存在のすべての可能性に広がっているが、その存在が失われることなく、その存在が維持されていると言えるでしょう.
実際、総確率が減少すれば、そのシステムは存在する可能性が低くなり、存在する確率をゼロにすることで、消滅してしまうことになります ! 状態や波動関数の振幅は、波のピークやトラフのように正または負になることがある.
そのため、確率の振幅はマイナスかプラスのどちらかになり、水素分子の結合状態と非結合状態をプラスとマイナスという記号で表現している。 .
(. états molécule hydrogène ピタゴラスイッチ) しかし、振幅の2乗である確率は (または標準の2乗 )は常に正であり、これは確率的には正常である。.
確かに、ある確率、その次に確実でない確率、不確実な確率、あるいはゼロの確率を想像することはできるが、負の確率は意味がない。.
一方、確率の振幅はマイナスになることもあります.
ここで、2つの等しい確率振幅があるが、符号が逆で、互いに向かって伝播しているとします。 (彼らは波である).
これらの振幅が同じ場所にあるときの確率を考えると、逆符号の振幅は打ち消され、その2乗も0になる.
何かを観測する確率はゼロになる.
しかし、振幅が分離している場合、その二乗は正になる (多ければ多いほど良い、少なければ少ないほど良い)したがって、何かを観察する確率はもはやゼロではないだろう.
私たちが量子力学について語るとき、その確率的な性格を偶然のゲームのように考えるが、一般に無視されているのは、これらの確率がもっと不穏なものによって支えられていることであり、それが確率の波の振幅で、量子力学の現実性を与えているのである.
という式を考えてみると |ドッグスL ><ドッグスL | ケットとブラで構成され、ケットに適用される |ドッグス > となる。 |ドッグスL ><ドッグスL |ドッグス > どこ <ドッグスL |ドッグス > が得られる確率の振幅である。 |ドッグスL > ということで : |ドッグスL ><ドッグスL |ドッグス > = |ドッグスL >アル =アル |ドッグスL > が最終的な状態であることがわかります。 |ドッグスL > 確率に関連する アル という表現があります。 |ドッグスL ><ドッグスL | は、したがって、初期状態を変更した演算子 |ドッグス > を最終状態へ |ドッグスL > で、これが確率的に アル.
それは、ある観測中にシステムが束縛エネルギー状態へと進化した進化演算子.
これは当然、測定中にシステムがどのように進化するかを説明する第5の定説につながります.
次のような演算子を考えてみましょう。:
|ドッグスL ><ドッグスL | |犬 nl ><犬 nl | の固有状態への進化演算子の和である。 (ここで、エネルギー :奔放自在).
この演算子をketに適用すると |ドッグス >において :
( |ドッグスL ><ドッグスL | |犬 nl ><犬 nl | ) |ドッグス > または |ドッグスL ><ドッグスL |ドッグス > |犬 nl ><犬 nl |ドッグス > となる |ドッグスL >アル |犬 nl >アンル いやしくも アル |ドッグスL > アンル |犬 nl > という状態を分解したものである。 |ドッグス >自身のエネルギー状態の総和として |ドッグス > =アル |ドッグスL > アンル |犬 nl > オペレータが状態を変化させていない |ドッグス >が、単に個々のパーツに分解しているだけなので、「単位分割演算子」と呼ばれます"。.
状態のベクトル表現とその直交基底による分解によって、確率の振幅、つまり測定中のシステムの進化の確率を自然に表現できるのは興味深いことです.
Postulat_V
測定 :波束低減 ベクトルで表される系で、時間tに物理量Aを測定した場合 |Φ>が固有値 An となる場合、測定直後のシステムの状態は、An と関連する固有空間に射影される。 この仮定は「波束減少仮定」とも呼ばれる"。.
まず、この部分固有空間"の概念について説明します。.
これは、状態を固有状態に分解することの一般化に過ぎない.
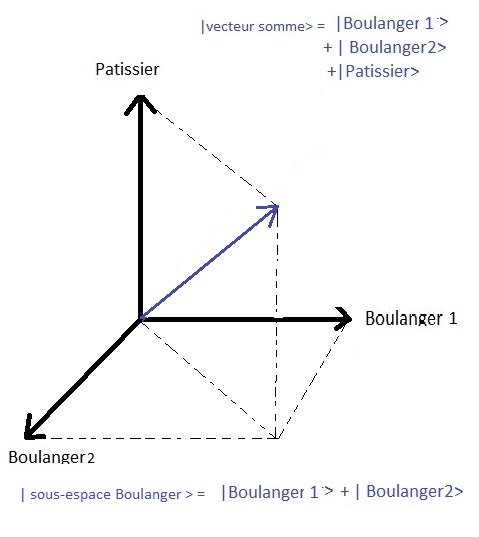
パンの例に戻って、パン職人2人とパティシエ1人の場合を見てみましょう。.
貿易の種類の区別が観察できない場合 (は、システムの観測値ではありません)計測の場合、パン屋1かパン屋2かを区別する必要はなく、パン屋自身の部分空間に状態が投影されたことが分かれば十分であり、実際、下図ではパン屋が住む水平面に相当している ! もし、どのパン屋からパンを買ったかを観察できる観測器があれば、この測定中に状態はどちらかのパン屋に投影され、測定の不確定性を取り除くことができるだろう.
しかし、もし系のこの性質が観測されなければ、系はこのベーカー波動関数の重ね合わせの状態のままである。.
この状態は縮退していると言われています.
実際には、複数の固有状態が同じ固有値を持つ場合、その固有値は (同気)これらの状態は縮退していると言われています.
縮退した状態のエネルギーを変化させ、等価でなくなるようなエネルギー制約をシステムに加えることで、縮退を解消することができます.
量子物理学は、本質的に共鳴で構成されるミクロの世界の構造を理解することを目的としています (スタンディングウエーブ)の固有値であり、システムの全エネルギー演算子である (ハミルトニアン).
 第5の仮定は、測定中に系の状態が、固有値が測定された状態に向かって進化することを述べている。.
第5の仮定は、測定中に系の状態が、固有値が測定された状態に向かって進化することを述べている。.
ベクトル射影の幾何学的表現に物理的な実在性を与えるのは、いわゆる「波束の縮小"」あるいは「波動関数の崩壊"」のポスチュレートで、この操作で系が物理的に進化するからである。.
非量子物理学の理論では、系の進化を担うのは力学方程式だけであるのに対し、観測によって系が進化するという事実を導入したことは、おそらく量子力学の最大の概念革命であろう.
従来、力学系の方程式は、エネルギーが系にどのように作用して系を変化させるかを表現するものであった.
この第5ポスチュレートでは、測定そのものがシステムを変形させることを見てきた.
量子力学の場合、このような動的方程式も存在し、次のように呼ばれる。 シュレーディンガー方程式 .
したがって、力学的には、進化には2つのメカニズムがある。:時間の中のエネルギーの作用と時間の外の観測の作用.
この方程式は、量子力学の第六、最後の仮定を構成するものである。 (下記参照).
第5の仮定は、システムの観察者がシステムの進化に関与することである.
このように、量子力学では、観測者はもはや物理系から独立していないのです.
観測者と物理系は不可分の全体を形成している.
観測者はシステムに組み込まれていると言えるかもしれません (が、量子もつれの意味ではなく、波動関数にのみ関係する).
量子もつれという現象は、複数の粒子からなる量子系が1つの波動関数で記述されることに起因すると前述した (一義)物理空間上で粒子が遠ざかったと思われる場合でも.
第5仮定によると、測定中に波動関数が適切な部分空間に縮退し、システムを構成するすべての粒子の状態に同時に影響を与える。.
アインシュタインは、量子力学が持つこのような意味合いは、光速で定義されるあらゆる物理的相互作用の伝搬限界に反すると考え、決して認めることができなかったのである。.
アインシュタインの相対性理論によれば、エネルギーが光速より速く移動することはありえない.
光は明らかに光速で進むが、それは純粋なエネルギー、すなわち質量を持たないからこそできることである。.
したがって、質量粒子は必然的に光速よりも低い速度で移動しなければならない.
この量子パラドックスの物理的な解決は、「量子力学的パラドックス」と呼ばれる実験によって行われた。expérience_d_Aspect.
この実験によって、波動関数が私たちの住む物理的な空間には依存しないことが明白に証明されたのです:観測による崩壊時の進化は、空間上のどの地点でも同時に行われる.
アスペクトの実験は、より高度な条件下で何度も再現され、量子力学の限界に挑んできたが、一度も屈することはなかった。 ! 量子論は非局所的な理論であると言われている.
非局所性」または「非分離性」という用語が使われますが、これは同じ意味です。.
アインシュタインの相対性理論以来、空間と時間は同じ深遠な現実の一側面であると考えなければならないからだ。 :じくうせかい.
アスペクトの実験に続いて相対論的な枠組みで行われた最近の実験では、相対論的な枠組みでの量子もつれの有効性が確認されている.
(シーエフ Expérience_d_Antoine_Suarez物理学者のホームページで発見 Philippe_Guillemant量子的な現実を統合するビジョンを提供する ) 物理の実験では、ある範囲内の値しか測定できないので、この最後の実験が重要である.
このように、最初のアスペクト実験では、相関光子用の検出器 (1つの量子状態で)数メートルしか離れていない.
これは、量子もつれが未知の物理現象によるものではないことを証明するのに十分であった。 (かくれへんすう)亜光速で.
そのような現象の速度は、必然的に超光速になるのです.
このような超光速は、アインシュタインの相対性理論によってほとんど認められないが、アスペクトの最初の実験では、この可能性を完全に否定することはできなかった.
アントワーヌ・スアレスの実験では、相関のある2つの光子の検出の間の因果関係の可能性さえも抑制されるからだ。:どちらの光子も、同じ時間枠で検出されないため、前にも後にも検出されない.
相対論的量子論では、最初の仮定で見たように、波動関数はもはや時間には依存しない。.
その理由は、時間が位置と同じレベル、すなわちシステムの観測可能な性質に還元され、波動関数がシステムの性質に依存しないためである (第二前提).
このような理論では、波動関数は次のようになります。 |ドッグス >となり、もはや |サイ(t) > .
時間は、位置Pと同じように、観測可能なTとなる。.
L_expérience_du_chat_de_Shroedingerは、物理学者によって考案された思考実験です。 Erwin_Shroedinger第5ポスチュレートに直接関連する量子力学における測定の問題を考察するために.
この完全に非現実的な思考実験を本物の猫を使って行ったのは、量子力学における観察者とは何かということを考えさせるためです。.
あなたは、測度に関するポスチュレーションで見たように (または観察)オブザーバーが何であるかを詳しく説明しないことを.
ポスチュレートは、測定を行う観測者が存在することを述べているが、観測者の性質については、それ以上何も述べていない。 ! この実験では、猫を箱の中に隔離し、観察できないようにします (定量的)何らか.
これは、猫が量子力学によってよく記述される原子から構成される物理システムであると先験的に考えることができるにもかかわらず、実際にはそうではないことを仮定している.
この部屋には、猫にとって致命的なガスの入ったバイアルと、粒子を検知するとバイアルを開ける粒子検知器も設置されている.
粒子が検出されると猫は死に、検出されないと猫は生きる.
我々が猫の健康状態を観測していない限り"量子的に"観測可能な固有状態の重ね合わせとして知られる一般的な量子状態のままである。 |生猫 > と |チャット・モーション > ということで |喋る > = |生猫 > |チャット・モーション > 私たちの量子力学システムは、いくつかのコンポーネントで構成されています。:猫、検出器、粒子.
これらのサブシステムもすべて波動関数の確立のために考慮しなければならないので、次のようになります。: |粒子 > = |粒子存在 > |ないじょし > と |センサー > = |じょうたいせいりゅうし > |ふかくじつせいりゅうしじょうたい > 量子力学に関連する数学は、私たちが"shroedinger"と呼ぶ大域的なシステムを示しています。 : |シュレディンガー > = |猫, 検出器, 粒子 > = |喋る>¤ |センサー >¤ |粒子 > ここで,¤は状態ベクトルのテンソル積"である。.
同じ量子状態であることから、これらの異なるサブシステムは複雑であると言われている.
この商品は、通常の商品取引と同様に、流通性があります :A * (B C ) =A*B A*C 量子力学の用語では、一般的な量子状態を展開することができます。.
まず、検出器と粒子のみからなる系から始めましょう.
|検出器、粒子 > = |センサー >¤ |粒子 > = ( |じょうたいせいりゅうし > |ふかくじつせいりゅうしじょうたい > )¤ ( |粒子存在 > |ないじょし > ) 開発によって :
|検出器、粒子 > = |じょうたいせいりゅうし > ¤ |粒子存在 >
|ふかくじつせいりゅうしじょうたい >¤ |ないじょし >
|ふかくじつせいりゅうしじょうたい >¤ |粒子存在 >
|じょうたいせいりゅうし > ¤ |ないじょし >
Erwin Shroedinger nweb 最初の2つの状態は簡単に理解できる。粒子が存在すればそれが検出され、存在しなければ検出されないのは論理的なことである.
次の2つの状態は、非常にありえないが、それでも量子力学によれば存在する。.
国家に対して |シュレディンガー > その結果、8つの固有状態(うち2つは可能性が高く、6つは可能性が低い)を持つ波動関数が導かれることになる。.
という2つの状態が考えられます。:
|チャット・モーション >¤ |じょうたいせいりゅうし >¤ |粒子存在 > |生猫 >¤ |ふかくじつせいりゅうしじょうたい >¤ |ないじょし > 私たちがシステムを観測していない限り、例えば箱を開けることに相当するのですが、私たちは猫が不確定な生命状態にある重ね合わせの状態にあるのです.
ここにパラドックスがある.
しかし、さらに推論を進めると、物理学者が行ったのは次のようなことです。 Eugène_Wignerノーベル物理学賞.
これは théorie_de_l_influence_de_la_conscience 彼は、猫の生死を見る観察者の目も、次の2つの状態を持つ量子系であると考えたのです。: |油絵 > = |めはねこをみる > |目は口ほどに物を言う > そして、完全な波動関数の状態には、目が死んで見える、猫が生きて見えるといった"幻覚的な状態が含まれることになります。...
しかし、同じく原子で構成される観測者の脳までの測定の連鎖を考え続けることも可能です.
そこで質問ですが :実際に測定が行われるとき、つまり波動関数の崩壊が起こり、その結果、実験結果が選択されるとき:生死不明猫.
ウィグナーは、すべての物質が量子力学によって記述可能であり、したがって波動関数の一部であるため、物質的なものが崩壊を引き起こすことはないと言っている。.
もし物質的なものが測定を操作しないなら、それを行う非物質的なものが残るだけで、ウィグナーはこれを意識と同定し、最終的に観察者が何であるかを同定するのである.
彼の解釈では 観察者は意識 .
観測者と波動関数の関連性に注目:ともかくも ! この2つの間にあるものこそ、マテリアルであると言えるかもしれません。:観測.
このことは、物理学者によって導入された「独立した現実」または「隠された現実」という概念に近いものである。 Bernard_d_Espagnat量子力学の哲学的な理解のために.
bernard_d_espagnat_physique_quantique_et_réalité_la_réalité_c_est_quoi ;https://www.
動画.
com/watch?v=Jd8FiWJ5v8M; これはまた、古代インドのヴェーダで、物質的な現実を「マヤ」または「感覚の幻想」と表現した概念に近づけるものでもある。.
このマヤは、3つの要素の無限の相互関係によって作られています。 :りち、ちゃんだ、でばったとは、主体、客体、それらの関係、知識 (霊的:しんりょうふう)または認識 (物質:素材の).
意識観察者と非物質的量子現実が現象学的物質現実を創り出す.
この点で、映画『マトリックス』は現実の寓話である。ただ、重要な違いは、幻想の現実を作り出すのが機械ではなく、意識そのものであることだ.
したがって、意識とは、知覚や知識を通じての対象との関係であると定義することができる.
以下のトライアドは等価である。:
samhita_tab_ja
ヴェーダ 哲学 量子物理学
りっし 題目 オブザーバー 目利き オブザーバー
ディビジョン パーセプション (主客関係) 観測 知識 可観測 燭台切 物 かんしゅ 既知 測定結果:観測値の固有値
波動関数と意識は、物質性を超越した同じ現実の表裏一体であり
この物質性の原点にある.
むろん物理学者全体が、量子的な現実についてそこまで考えているわけではありません。.
この辺りの標準的な位置づけはinterprétation_de_l_école_de_Copenhague.
この立場では、2つの測定の間には物体は存在せず、存在するのは観測された物体だけであると言う"。.
この立場は、古典的な世界を経験し、それを絶対的な基準として考える人間の観察者の状況から生まれるものである.
古典的という言葉は、人類全体が同じように認識していることに対応するものである.しかし、この立場は相反するものです。
りょうじつ.
この位置からの距離の異なる度合いを定義することができます。:
- 第一次は、このポジションに完全に集中しており、それ以外のものがあることを認めようとしない
絶対的な客観的な物質的現実があること.これが唯物論的見解である.
なお、この考え方は、アスペクトの実験が力学を検証して以来、科学的には通用しなくなっている。
という、最も気になる記述があります。.
同時に、この量子力学は、科学史上最も検証された理論でもあります.
このように、この視点は単純な"唯物論的信念に還元される"。.
しかし、残念ながら、アインシュタインは、そのようなことを考えるほど長くは生きられなかった。
物理学者ポドルスキー、ローゼンとともに、有名な論文で定義したパラドックスを、アスペクト実験によって解決したことをご覧ください。:
その Paradoxe_EPR.
- 第二段階は、まだ一部の人にしか知られていないコペンハーゲン学派の解釈です。
有識者(物理学者、哲学者を中心とした少数派.
ここで、私たちが住んでいる古典的な世界は、もはや世界の全体像を表していない。なぜなら、そこには
という、まったく不思議な量子世界です。
量子論による.
- 第三次では、古典的な世界は原子そのものが粒子で構成されていると考える。
古典の世界の基本は、量子の世界です。
ということで、正当に絶対的な基準となるべきものである。.
私たちが知っている安定した物理世界は、たった3つの量子粒子から構成されている:電子・陽子・ニュートリノ.
この第3の視点は、最終的かつ単純に、次のように言って、すべての量子パラドックスを取り除くものである。
やくそくをこえる (クラシック)量子論の、しかし、単純に受け入れなければならないこと
ありのまま (コペンハーゲ)と、ようやくその位置づけの優位性を認識する。.
したがって、量子モデルには決して不具合が生じないことが予測される.その発足以来、量子的な現実がどのようなものであるかが次第に明らかになってきています。
私たちを取り巻く世界、とりわけ生命という巨大で一貫性のあるシステムの理解に介入しています。...量子.
かなり最近の例として、以下の2つがあります。:
Postulat_VI 量子状態の時間発展.
国家 . Phi
は、非相対論的量子系の時間依存シュレーディンガー方程式の解である。:
_ H |ファイ(t)> =i h/2*π d |ファイ(t)>/ dt
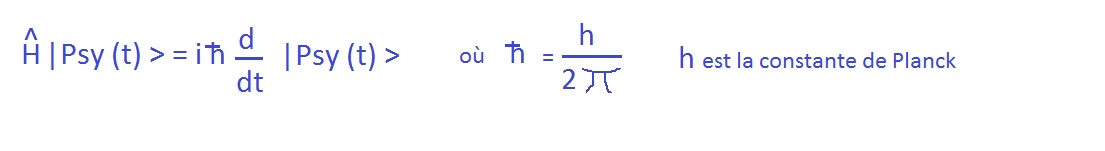 第6のポスチュレートは. équation de Schrödinger
.
第6のポスチュレートは. équation de Schrödinger
.
これは、量子力学の動的方程式である.
これは、システムの「全エネルギー」演算子、つまりハミルトニアン("H^)が、システムの時間発展を担っていることを意味します。.
(伝統的に量子力学では、演算子は固有値のような他の数学的対象から区別するために、帽子を与えられています。.シュレーディンガー方程式) この式の形は、ハミルトン演算子をシステムの波動関数に適用することで、その時間に関する微分、すなわち時間的にどのように変化するかを得ることを示している.
(デルタtの時間変化に対して "dt" 変化がある "d |サイ(t) >波動関数の).
そこで、ハミルトニアン演算子を適用すると (エネルジー)を波動関数に変換すると、その時間発展が得られます。.
物事を実現するのはエネルギーであることは明らかである.
エネルギーと時間は本質的に結びついている.
これらは共役変数の組を形成すると言われています.
この式は、非相対論的な枠組みにおいてのみ有効である.
相対論的な枠組みで有効な方程式は、Klein-Gordon 方程式.
シーエフ Olivier_castera_free_Equation_de_Schrodinger_pdf ハミルトニアン演算子Hは、系に介在するすべてのエネルギーで構成される.
これらのエネルギーには2つの種類があります。:うんどうエネルギーと位置エネルギー.
運動エネルギーとは、動いている質量に含まれるエネルギーのことです.
窓から投げ入れた小石が、ある速度を与えられたときに得た運動エネルギーによって窓を割ることができる.
ガラスが何枚か続いている場合、石の速度が大きいほど、より多くのガラスを通り抜けることができる.
ポテンシャルエネルギーは、システムに適用される力場によるものです.
地上にある窓ガラスの上に小石を落とすと、地球からの距離によって持つ重力位置エネルギーにより、速度が増す。.
時間が経つほど、位置エネルギーは運動エネルギーに変換され、小石は地面に到達したとき、失った位置エネルギーよりも得た運動エネルギーによって窓を割るのです.
もし、井戸の中に押し込めば、位置エネルギーを完全に使い果たすまで、同じプロセスを続けることができるだろう(可能であれば)。.
振り子の動きを考えてみると (珠玉の一品)後者は振動する、つまり開始位置から (俯せにする)小石を落とすと、小石は紐が垂直になるまで加速し、その後、反対側で開始位置と対称的な位置で垂直に止まるまで減速します。.
振り子は、位置エネルギーを運動エネルギーに、運動エネルギーを位置エネルギーに変換し、これを周期的に繰り返す.
他の力が加わっていない場合は、動きが止まりません.
実際には、常に摩擦力があり、エネルギーがなくなるまで熱として放散されます。.
しかし、この最後の点は古典力学においてのみ当てはまることで、量子力学においては摩擦は存在しないのです ! 位置エネルギーと運動エネルギーの間で循環的な変換が行われるもう一つの系は、例えば月と地球のように、惑星の周りを回る衛星の運動である.
この場合の古典力学の解は、衛星の軌道が楕円であること、すなわち、月が地球から最も遠くなる瞬間があることを示している (最大位置エネルギーと最小運動エネルギー、遠地点)と、月が地球に最も接近する時間帯があります (位置エネルギーが最小で運動エネルギーが最大、近地点).
今説明した系は古典的な系ですが、量子的な領域にも対応するものがあります.
例えば、量子力学における振り子モデルは調和振動子と呼ばれ、衛星モデルは水素原子モデルに相当する:衛星電子.
量子力学では、運動エネルギーは質量を含む演算子であり、位置エネルギーももちろん演算子で表されるが、その形式は関与するエネルギーに依存することになる:電位、磁位。 ...
シュレーディンガー方程式における質量の扱い方は、波と胴体の二重性を確立したルイ・ド・ブロイの初期の研究に由来している。:を、質量に比例した周波数の波として扱うことができます。.
これは、2つのエネルギー計算式に基づいています。:E =m c² これはアインシュタインの特殊相対性理論のエネルギー公式である :は、質量がエネルギーEに相当します。 =h * nu これは光電効果を説明するプランク-アインシュタインの関係である :エネルギーは周波数に比例する.
このように、シュレーディンガー方程式には、アインシュタインの特殊相対性理論の結果が統合されていることがわかります。.
重要なことは、エネルギーが系に制約を与えること、すなわち波動関数に影響を与えることを理解することです.
高調波発振器のような振動系を扱う場合 (ひもつき)または水素原子 (衛星)エネルギー制約の効果は、波動関数を空間のある領域に局在化させることである.
例えば、力を受けない古典的な系は (星の重力が無視できる星間空間で流星を見失い)は無限に直線的に移動する.
量子力学に相当するのは、力を受けずに無限に伝播する光子のような平面波である (光子は質量や電荷を持たない粒子であるため、いかなる力やエネルギーも受けない。).
波動関数が周期的な解を持つ場合 (きょくしょはかんすう)時間はもはや、システムの各パーツを無限に遠ざける効果を持っていない.
電子は原子核(水素原子の場合は陽子)の近くに留まります。.
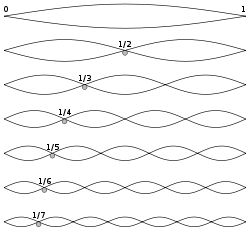
同時に、量子波が有限な領域を周期的に伝播する場合、それ自体が重なり合うため、建設的または破壊的に自分自身と干渉することになる.
このような系のシュレーディンガー方程式を解くと、波動関数の形にはもはや時間は介在せず、ただ空間 (首位)波の形状を決定する.
の場合です。 ondes_stationnaires_ja既述の.
つまり、干渉が建設的である場所と破壊的である場所は常に同じであるということです.
定在波は、動的な現象から静的な現象が生じることを理解することができる強力な概念です.
これは量子ビジョンの統合を可能にする要素の一つである:我々が経験する物質の安定性は、常に動いている波のもつれからきているが、その干渉の結果は安定している。.
原子の場合、シュレーディンガー方程式の解関数である原子軌道によって、その形状が明確に定義される。: 電子の存在する確率の雲である。.
雲の密度が高いほど、電子が存在する確率が高くなる.
 定在波の確率的な振幅の表現 (ハーモニックス)高調波発振器の.
定在波の確率的な振幅の表現 (ハーモニックス)高調波発振器の.
振動状態との類似性に注目 (振動ノードと腹部)弦鳴.
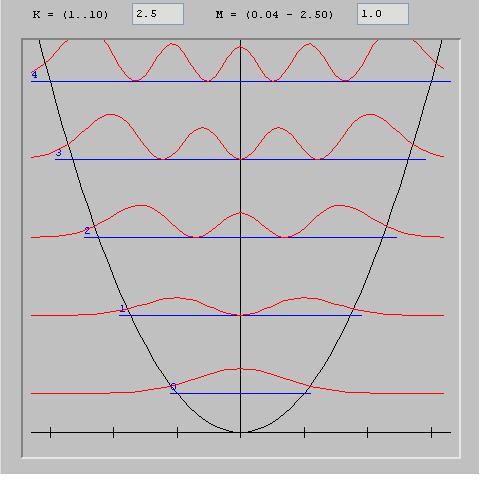
 我々は、量子の場合 (左)波動関数の確率振幅 (朱色で)は中心から遠ざかるにつれて徐々に減少し、すなわちポテンシャルが強くなる領域では (黒色放物線)が、完全にゼロになることはない.
我々は、量子の場合 (左)波動関数の確率振幅 (朱色で)は中心から遠ざかるにつれて徐々に減少し、すなわちポテンシャルが強くなる領域では (黒色放物線)が、完全にゼロになることはない.
つまり、古典的にはポテンシャルが運動エネルギーよりも低い領域に捕捉されるのに対して、ポテンシャルエネルギーが運動エネルギーよりも高い遠隔の領域で粒子が発見される可能性があるのです。.
この事実があるからこそeffet_tunnel波動関数がゼロでないため、粒子のエネルギーよりも高いエネルギーのポテンシャル障壁を越えて、粒子を観測することができる。.
これは、波動関数の非局所的な側面の結果である.
これは、エネルギーが波動関数に与える制約で、波動関数は局在化したまま、それ自身と干渉して、特定のエネルギー値に関連する定在波を発生させる。 (したがって、定量的な値)という、量子化という概念の原点となるものです。.
最後に、量子論の原点は何かということをお話しする必要があります:その constante_de_Planckというシュレーディンガー方程式に登場する.
この定数は物理学者によって導入された Max_Planck物質からの熱放射の値を温度の関数として説明するために.
この放射が従う法則から、熱エネルギーは連続的に放出されるのではなく、パケットまたは^クアンタ^で放出されると考えざるを得ない。.
物質の量子的性質を示す最初の証拠である.
物理学では、作用はエネルギーと時間の積として定義される.
かなり直感的に操作できる:あるエネルギーがある時間作用すると、そのエネルギーと作用した時間の長さに比例した値を持つある作用を発生させる。.
プランク定数は、物理世界で起こりうる最小の作用を表します。.
現実の量子的性質を特徴づける物理学の普遍定数である.
この定数の値は極めて小さい: 6.62607004 × 10-34 m2 kg / s にもかかわらず、0でない.
0,000000000000000000000000000000000662607004 この定数を光速や万有引力定数などの他の基本定数と組み合わせると、物理学のさまざまな単位の最小量が推論される。 :プランク長、プランク時間など。...
で、これはプランク単位と呼ばれる.
したがって、量子力学によって記述される物理的世界は、無限に小さいという限界があり、それを超えるともはや物理学の用語で語ることはできない、それはついに物理的世界の端となるのだ.
もしエッジ、つまり限界があるとすれば、それは波動関数に対する自然な量子的制約であり、したがって量子化に対する制約である (というのは、それ自体、見てきたように、力).
プランク定数は宇宙の画素を定義する.
定量化の最も根本的な起源は、本来連続的でない意識の働きにも見出すことができる.
実際、意識における視点である対象を主体が観察することを考えるなら、それは、意識が異なる可能性のある視点を識別することによってのみ可能なのである.
そうでなければ、すべての視点が融合してしまい、本当の意味での観察ができないからです。.
識別は、この意味で意識の基本的な特性である知性の質である.
このように、測定の量子ポスチュレートに存在する要素を見つけることができます。.
以下は、すべての前提をひとつのアフォリズムにまとめる試みです。:
"良心の眼差しのもと、可能なことだけが成される.
"
1.5.1.格言の分析
詩 量子マッチング きてい
とは 波動関数、状態ベクトル、または "ket^ (ブラケットから、フランス語でフック) . Premier postulat
可能 波動関数の確率的な構造、ケットの異なる可能性のある固有状態 . Troisième postulat はかどる 進化を担う系のハミルトニアン演算子全エネルギーのダイナミックス. . Deuxième postulat りょうしんちゅう 測定の前提条件、すなわち観察者の必要な介入 . Quatrième postulat 成せば成る は観測値の固有値のみであり、システムの状態は対応する固有状態の. . Cinquième postulat 可能なことは、実現する シュレーディンガー方程式、量子力学方程式. . Sixième postulat
量子力学は、現代科学の時代における最大の革命である。なぜなら、それは唯物論の立場を決定的に破壊し、科学と意識が再び一体となる人類の発展への道を開くものだからである。.
科学者が量子論のメッセージを受け入れることが非常に困難であることが、量子論にアクセスできる人が非常に少ない理由を説明しています。.
ここでは、Jean Stauneが分析し、Bruno Lussatoが報告した、この状況の概要を紹介します。: bruno_lussato_les_plus_grandes_désinformations_de_l_histoire_des_sciences
(アラン・アスペクトが1982年にフランスの大学を回って研究成果を発表したトゥールーズでの会議の様子を、2009年のブログに残しました。.Bruno Lussato 科学史上最大の誤報 Nweb) この文章は、科学界の一員である多くの知識人たちによって書かれ、おそらくずっと良いものになったはずです"しかし、彼らがそれを嫌がったために、私は一方ではドメイン名量子を予約することができました。.
一方では、不思議なことに入手可能だったこのテキストを何十時間もかけて推敲し、おそらくまだ改善されるはずです。...
アインシュタイン-ポドルスキ-ローゼンのパロディに決着をつけた決定的な実験
1982年、オルセーの量子光学センターの研究者兼実験者であったアラン・アスペクトによって作られた
は、フォトンをベースとした.
基礎となる理論の詳細な説明は書籍に記載されています ベルナール・デスパニャー著^^A la recherche du réel^^。.
その年、私は大学にいて、アラン・アスペクトがプレゼンに来てくれたんです。
その成果は、トゥールーズにあるポール・サバティエ大学のマックスウェル円形劇場で発表されました。.
明確な測定結果を提示した後、彼は去っていった。
ぎゃふんと言わせる会 (講演会場は、教授や研究者の方々でいっぱいでした。).
プレゼンテーションの最後、重要な沈黙の時間を経て、フロアが開かれたとき、スピーカーはこう言った。 という質問に対して、たった一人の研究者が立ち上がりました。 (私の相対性理論の先生)という質問をし、このような質問をしました。:
そして、今、それを受け入れるのは簡単なことだとお考えですか?.
アスペクトは、「そんなことは言っていない、自分がやったことだ」と抗弁した。
という実験であり、その結果がそれであったこと、しかし、そのようなことがないように注意したこと。
釈明を垂れる.
何年か後に、一緒にいた人から知ったのですが、彼は
プロアインシュタイン派で、量子力学が挑戦されることを期待していたこと.
サイドベイの3列目に一人でいたのですが、よくわからなくて面食らいました
なぜ問題視されるのか、いや、むしろよくわかりました.
実験はまだ始まったばかりだが、結果が出るのは時間の問題だった頃。
論戦は硫黄を含む非常に強いものになった.
物理学者の科学界がショックを受けていた時、私たちは
先が思いやられる.
情報を消化するのに時間がかかった、2020年の状況を見ることができます。 エコール・ポリテクニークで行われたこの講義をご覧ください。 by Hervé Zwirn(CNRS研究部門ディレクター
_x_sciences_de_l_homme_et_de_la_société_x_shs_mécanique_quantique_le_monde_existe_t_il
この経験には (を持つべきであった。)にも同じような効果があります。
電波の発見は、物理学者にとって (でんじは)をお持ちの方
電磁場という抽象的な概念に、より鮮明なリアリティを与える。.
非分離性の発見とその観察について
物理的なレベルでは、独立した現実という概念に生命を与える、すなわち
空間と時間に依存しない現実の、すなわちすべての
時空間偶発性、すなわちすべての物理的偶発性.
力学の第一仮定から導き出される第一の結論 やんけ:
量子系の実態 (そして、結局はすべてのシステムは量子である!x 人文・社会科学 x shs 量子力学 世界は存在するか nwebs)が下支えしています。
それ自体では観測できない抽象的な可能性空間によって (非物理的で
じっぽうふざい)が、しかし、それにもかかわらず、現実のものである。
この抽象的な機能のレベルから、具体的な現実が出現します。 (かんしゅ).
一言で言えば:を含むので、全知全能である。
非局所的に物理システムに関するすべての情報.
さらに、完全にするために、これは明らかに物理的であることができない観察者に関連している.
ポスチュレートは、明らかに物理システムに観測者を含んでいない
しかし、その存在は、観測が行われるために必要であると宣言しています。
ぶつりてきかいせき.
観察者と独立した現実が密接な関係を持っていることが明らかになる:
両者は非物理的であり、情報、知識、知覚の面で相互作用します。.
これは、シャーマンの考える「世界の夢"」と完全に一致する。.
この点で、映画「マトリックス」は量子的現実の寓話として見ることができる.
現実との違いは、ホログラフィック・シミュレーションの世界が製造されていないことです
物質的なコンピュータではなく、非物質的な宇宙的なコンピュータによって、自らを認識する。
広い意味での意識に.
この普遍的な意識は、あなたが好きなように名前をつけることができ、またつけてきました。
しかし、これらはこの意識の無限の力を使い果たすことはない。.