Los postulados de la mecûÀnica cuûÀntica
versiûô°n disponible en : en it ru zh ja de nl pt fr
fecha de creación : 20240724- fecha de actualización : 20240724- fecha de generación : 20241110_231431
Este artûÙculo presenta en detalle la postulats_de_la_mûˋcanique_quantique a partir de simples consideraciones matemûÀticas y geomûˋtricas y de analogûÙas tomadas de la vida cotidiana.
En fûÙsica se desarrollan conceptos relacionados con los objetos matemûÀticos para establecer teorûÙas que permitan representar el mundo fûÙsico a travûˋs de sus leyes de funcionamiento.
La mecûÀnica clûÀsica o teorûÙa de Newton es la teorûÙa que permite representar el funcionamiento de la materia a escalas sensibles a la percepciû°n humana y que llamamos macroscû°picas.
A escala cosmolû°gica, esta teorûÙa se generaliza a travûˋs de las teorûÙas relativistas de Einstein.
La relatividad general es la teorûÙa que mûÀs se ocupa de la fuerza de la gravedad.
La mecûÀnica cuûÀntica es la teorûÙa que permite representar el funcionamiento de la materia a nivel microscû°pico, aunque la frontera entre lo microscû°pico y lo macroscû°pico no estûÀ claramente definida en tûˋrminos de escala, por lo que podemos tener comportamientos cuûÀnticos a escalas macroscû°picas, como en el laser o el cables_ûˋlectriques_supraconducteurs La teorûÙa cuûÀntica no se ocupa de una fuerza particular de la naturaleza como la relatividad general, es mûÀs bien un lenguaje.
El lenguaje de los objetos cuûÀnticos.
AsûÙ, podemos aplicar este lenguaje a diversas fuerzas o sistemas, cuantificûÀndolos asûÙ.
El conjunto de conceptos cuûÀnticos gira en torno a seis postulados bûÀsicos que definen plenamente la teorûÙa cuûÀntica.cables elûˋctricos superconductores nweb Presentaremos estos seis postulados y trataremos de identificar su significado de forma sencilla.
La expresiû°n del primer postulado tal y como se define en el libro de Cohen-Tanoudji " MecûÀnica CuûÀntica Volumen 1" es :
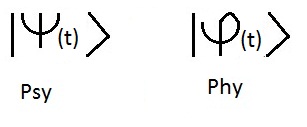
En un tiempo fijo t, el estado de un sistema fûÙsico estûÀ definido por los datos
de un ket o funciû°n de onda o vector de estado anotado |psy(t)> perteneciente al espacio de estados".
Postulado I nweb
La letra griega Psy se utiliza para designar la funciû°n de onda, nosotros utilizamos
tambiûˋn con indiferencia la carta Phy.

El primer concepto de la mecûÀnica se refiere a la representaciû°n del estado del sistema fûÙsico.
Esta es una forma natural de definir el objeto de estudio. AquûÙ simplemente decimos que el sistema existe
y que su estado puede ser representado por una funciû°n dependiente del tiempo
esto se debe a que el estado del sistema no es a priori estûÀtico sino dinûÀmico.
En la mecûÀnica clûÀsica el sistema fûÙsico estûÀ representado por el "punto material".
Un sistema complejo estarûÀ representado por un conjunto de puntos materiales conectados
entre ellos para formar un objeto sû°lido o no sû°lido (conexiones rûÙgidas o no rûÙgidas, por ejemplo: cristal o gas).
El primer postulado afirma simplemente que el estado del sistema en un momento dado es û¤nico
y pertenece a un conjunto de estados posibles agrupados en un conjunto
matemûÀticas llamadas " espacio de estado".
Hablamos de espacio y no simplemente de un conjunto porque el estado cuûÀntico es un vector
que es un objeto matemûÀtico que representa una direcciû°n en un espacio.
Todos conocemos el espacio tridimensional (longitud, anchura, altura o profundidad segû¤n la orientaciû°n de las dos primeras dimensiones)
Es el espacio fûÙsico en el que vivimos.
El espacio de estados en el que viven los sistemas cuûÀnticos " no es un espacio fûÙsico, es un espacio abstracto (Espacio de Hilbert)
y su dimensiû°n es infinita para representar la infinidad de estados posibles que existen incluso para los sistemas fûÙsicos simples.
Hagamos una analogûÙa con un ejemplo de la vida cotidiana
para entender cû°mo se modela un sistema cuûÀntico.
Imagina a una persona sentada tranquilamente en su piso y de repente
se da cuenta de que tiene que salir a comprar pan.
Se prepara para salir y en su mente sigue dudando sobre el lugar donde va a comprar el pan.
Tiene que elegir entre una panaderûÙa mûÀs arriba o una pastelerûÙa que tambiûˋn hace
que estûÀ mûÀs abajo de su calle.
Bajando las escaleras para salir, se puede decir que hay dos estados posibles en su mente que corresponden a las dos opciones de comprar pan. Estas opciones se pueden anotar de forma cuantificada:
estado 1: |panadero>
estado 2: |pastelerûÙa>
El estado de ûÀnimo de la persona es una combinaciû°n de estas dos posibilidades:
| Estatus> = |panadero> + |pastelerûÙa>
Los dos estados son completamente incompatibles: o compra el pan en la panaderûÙa, o en la pastelerûÙa. Ambas posibilidades tienen nada en comû¤n, no comparten nada. Geomûˋtricamente se dirûÀ que son ortogonales (perpendicular) y la representaciû°n geomûˋtrica en el espacio (de los estados asûÙ) serûÀ:
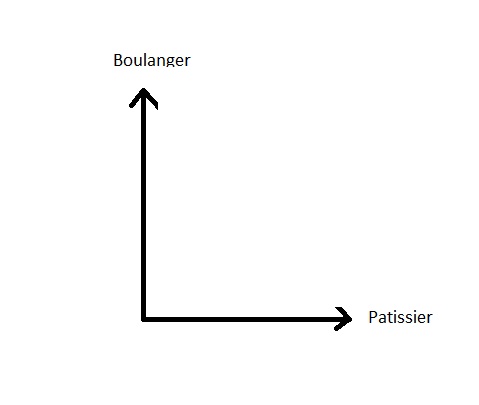
Por lo tanto, tenemos dos direcciones muy distintas que no tienen nada en comû¤n.
Si la flecha (vector) baker se inclinaba hacia la flecha (vector) pastelerûÙa
entonces esto significarûÙa que ir a comprar a
el panadero estûÀ un poco vinculado con ir a comprar
en la pastelerûÙa, que no es el caso, son dos
opciones incompatibles: ortogonales, es decir, en ûÀngulo recto: no comparten nada en tûˋrminos de liderazgo.
Por otro lado, el estado del sistema, es decir, el estado de ûÀnimo
de la persona es una llamada combinaciû°n lineal de los dos estados.
Decimos que tenemos una mezcla de estados. El verdadero estado mixto no
no se corresponde con nada observable: no sabemos
no donde se compra el pan.
Esta combinaciû°n lineal de las dos posibilidades corresponde a
a la suma de los dos vectores que representan los estados observables.
La suma de dos vectores se realiza de la siguiente manera : lo hacemos
Desde el final del primer vector y el segundo vector
suma resultante del principio de la primera y que termina hacia el final
de la segunda.
$BASE/fic/jpg/physique/etat_1.1.1.Somme_vecteur.jpg
Se dice que el espacio de estados es un espacio vectorial, es decir, un espacio de direcciones, esto implica que en la representaciû°n geomûˋtrica podemos mover los vectores sin cambiarlos naturaleza, siguen siendo los mismos vectores: apuntan en la misma direcciû°n. Tambiûˋn para simplificar la representaciû°n, todos los vectores parten del mismo punto para indicar que sû°lo las direcciones existen en este espacio. Esto se llama un espacio vectorial en contraposiciû°n a a un espacio de puntos que en matemûÀticas se denomina espacio afûÙn. ( La pantalla en la que que estûÀ leyendo este texto es un ejemplo de espacio afûÙn donde los pûÙxeles representan puntos en ese espacio.suma de estados vector img)
La representaciû°n geomûˋtrica se hace obviamente en un espacio de puntos porque un espacio vectorial
es una abstracciû°n pura y sû°lo puede representarse en el espacio que percibimos con puntos (posiciones) diferentes.
Pero esto no existe en el espacio de estados donde todas las representaciones de un vector en diferentes
las posiciones en el espacio de representaciû°n corresponden a un û¤nico vector en el espacio vectorial.
AsûÙ, el estado puede representarse de la siguiente manera :
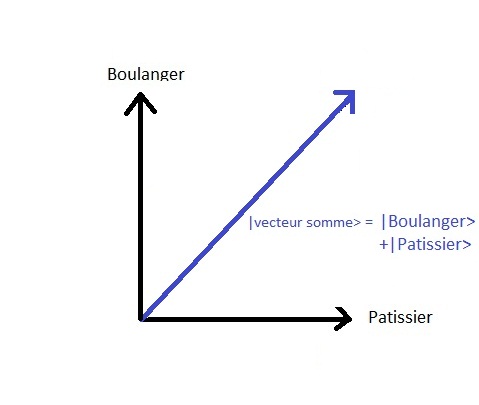
AquûÙ la dimensiû°n del espacio de estados es de dos. Si hubiera una tercera opciû°n
con otro panadero en una calle adyacente | panadero2 > entonces el espacio de estado serûÙa de dimensiû°n tres, etc..
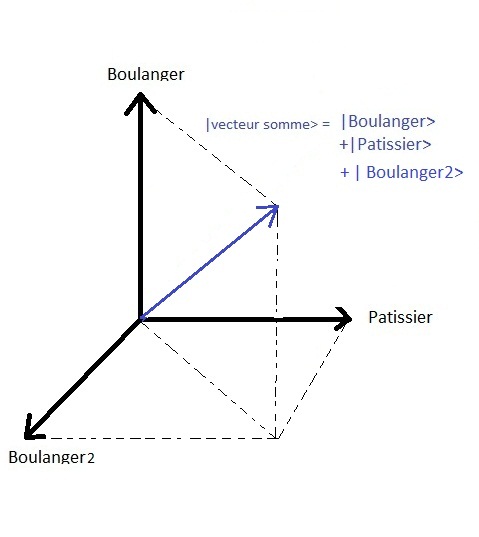
En fûÙsica, los sistemas de dos estados se pueden modelar de la misma manera.
Este es el caso de la molûˋcula de hidrû°geno ionizado. La molûˋcula de hidrû°geno
estûÀ compuesto por dos nû¤cleos de hidrû°geno, es decir, dos protones
y el hecho de que estûˋ ionizado significa que se le ha quitado un electrû°n
de los dos posee naturalmente. Por ejemplo
porque es simple : " a un solo electrû°n".
Los dos estados posicionales posibles para el electrû°n son :
La representaciû°n geomûˋtrica es:
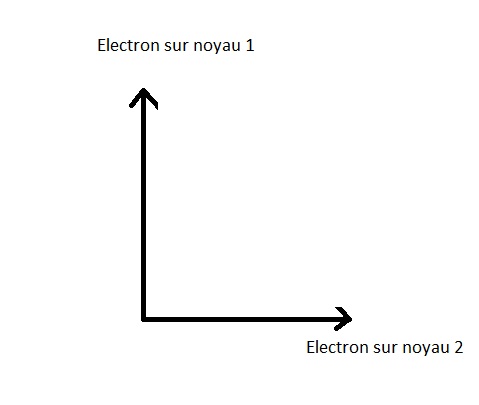
EstûÀ claro que el electrû°n no se puede encontrar (o mûÀs bien a encontrar, es decir : ser observado) al mismo tiempo en el nû¤cleo 1 y el nû¤cleo 2, estos estados son ortogonales.
En la expresiû°n del postulado se utilizan sinû°nimos para designar el vector de estado, que se denomina indistintamente
vector de estado, funciû°n de onda o ket. Estas diferentes denominaciones corresponden a diferentes aspectos matemûÀticos del vector de estado.
Veremos el aspecto de la funciû°n de onda en la explicaciû°n del segundo postulado y el aspecto del "ket" en el tercero.
En resumen, el estado cuûÀntico estûÀ representado por el vector dado (direcciû°n) en un espacio vectorial (de direcciones),
este vector se llama "vector de estado".
En la mecûÀnica clûÀsica, el estado estûÀ representado por el "punto material" que se define por sus propiedades fûÙsicas posiciû°n y velocidad.
Es importante seûÝalar que en la mecûÀnica cuûÀntica el estado del sistema es totalmente independiente del estado del sistema.
las propiedades fûÙsicas del sistema. El estado se define de forma abstracta y se podrûÙa decir "no fûÙsica".
Esto se detallarûÀ en la presentaciû°n de los siguientes postulados a travûˋs de la nociû°n de "base de representaciû°n vectorial del estado".
Pero se puede observar que el primer postulado hace que el vector de estado dependa sû°lo del tiempo y no de la posiciû°n
que es el espacio. Esto significa que la funciû°n de onda es no local.
Obviamente, la relatividad nos enseûÝa que el tiempo y el espacio forman un continuo y, por tanto, si una formulaciû°n de
la mecûÀnica cuûÀntica tiene en cuenta al menos la relatividad especial, el vector de estado no depende de
del tiempo. Esta teorûÙa es la electrodinûÀmica cuûÀntica o teorûÙa cuûÀntica del campo electromagnûˋtico.
La relatividad especial estûÀ muy ligada al electromagnetismo por el hecho de que Einstein elaborû° esta teorûÙa
para eliminar las paradojas que la teorûÙa electromagnûˋtica de Maxwell planteaba.
Los conceptos cuûÀnticos no fueron concebidos por pura imaginaciû°n. MûÀs bien, se han forjado en el fuego de la experimentaciû°n
de la microfûÙsica que requerûÙa que estos conceptos se representaran adecuadamente.
Aunque sea totalmente abstracto, el estado cuûÀntico es, sin embargo, real.
Esta realidad del estado cuûÀntico es lo que a menudo resulta mûÀs difûÙcil de admitir, aunque sea inevitable.
El funcionamiento de la materia, que es lo mûÀs concreto, se rige por algo totalmente abstracto.
Sin embargo, es imposible sortear esta dificultad ya que este concepto cuûÀntico es extraordinariamente sû°lido.
La situaciû°n cognitiva es algo similar al descubrimiento de las ondas electromagnûˋticas. Estas ondas fueron primero teû°ricamente
descubierto al combinar las ecuaciones de Maxwell que describen los campos elûˋctricos y magnûˋticos.
Su combinaciû°n proporcionû° una ecuaciû°n de propagaciû°n de ondas con una velocidad constante. Era una nociû°n abstracta
y nuevo, pero los experimentos han demostrado que los campos elûˋctricos y magnûˋticos producen ondas
que podûÙan ser controlados y utilizados, lo que llevû° a la comunicaciû°n por radio.
Hemos visto que esta velocidad es la velocidad medida de la luz.
Del mismo modo, el concepto tan abstracto de funciû°n de onda se ha convertido en algo muy concreto enintrication_quantique y dio lugar al ûÀrea tecnolû°gica de cryptographie_quantique
Postulat_II
" Cualquier cantidad fûÙsica observable 'a' es descrita por un operador 'A' que actû¤a en el espacio de estados; este operador es un observable.
" En la mecûÀnica clûÀsica hemos visto que son las propiedades del punto material, su velocidad y su posiciû°n las que determinan su estado.
Por ejemplo, la velocidad y la posiciû°n de una pelota en una pista de tenis o de un planeta en el sistema solar.
La posiciû°n y la velocidad de un objeto macroscû°pico se determinan en cada instante y esto define completamente el estado del sistema.
La evoluciû°n de la pelota de tenis en el espacio define en cada momento el estado del juego, si la pelota estûÀ en movimiento, "out" o no o inmû°vil en el suelo despuûˋs de haber cogido la red.
Y es la historia de sus estados la que define el partido y su resultado.
En cambio, en la mecûÀnica cuûÀntica, el estado general de un sistema reducido a una partûÙcula como el electrû°n del ejemplo anterior ya no estûÀ asociado a una posiciû°n o velocidad concreta, sino a una mezcla de todas las posiciones o velocidades posibles.
AdemûÀs, no podemos observar todas las propiedades del sistema al mismo tiempo como en la mecûÀnica clûÀsica.
Si el sistema estûÀ en un estado posicional, no estûÀ en un estado energûˋtico y viceversa.
En el ejemplo del pan tenemos estados posicionales que son el panadero y el pastelero que indican el lugar donde se compra el pan pero como veremos no son estados energûˋticos.
Al igual que en el ejemplo de la molûˋcula de hidrû°geno, el hecho de que el electrû°n se encuentre en el nû¤cleo 1 o en el nû¤cleo 2 representa estados posicionales, pero ûˋstos no son en sûÙ mismos estados energûˋticos de la molûˋcula.
En un sistema cuûÀntico las diferentes propiedades comparten el mismo espacio de estados, pero los estados correspondientes a las diferentes propiedades no estûÀn necesariamente representados por las mismas direcciones en el espacio.
Esto significa que si el espacio es bidimensional habrûÀ dos posibles estados posicionales pero tambiûˋn dos posibles estados energûˋticos y que los estados energûˋticos no tienen las mismas direcciones que los estados posicionales.
En el caso de la molûˋcula de hidrû°geno (ionizado) los posibles estados energûˋticos son:
| Estatus:ûˋnergie> = |estado relacionado> |estado no consolidado>
en la representaciû°n "dinûÀmica o energûˋtica" de la molûˋcula de hidrû°geno.
El estado general del sistema es completamente independiente de sus propiedades, por lo que para el pan podemos escribir:
| Estatus> = |determinaciû°n> |renuncia> = |panadero> |panadero>
Para la molûˋcula de hidrû°geno que llama El (estado relacionado) y Enl (estado no consolidado) los estados de energûÙa y P1 y P2 los estados de posiciû°n, tenemos:
| Estatus> = | El > | Enl > = | P1 > | P2 >
El hecho de que el estado sea independiente de sus propiedades observables y pueda expresarse independientemente de ellas es una caracterûÙstica fundamental de la mecûÀnica cuûÀntica.
Las propiedades estûÀn representadas por operadores matemûÀticos que, aplicados al estado cuûÀntico, determinan los posibles estados de esa propiedad.
Un operador en matemûÀticas es lo que hace evolucionar un valor en sentido amplio.
Por ejemplo, para la suma el operador "3 " aplicado a "2" da "3 2"="5" cambiamos el valor de "2" a "5" aplicando el operador "3 " (adiciû°n del valor tres) En la mecûÀnica cuûÀntica el operador hace evolucionar el estado.
El postulado dice que el operador "actû¤a" en el espacio de estados.
Sea P el operador de posiciû°n y E el operador de energûÙa (en realidad el operador de energûÙa se denota H para hamiltonien_es que es la funciû°n de energûÙa total definida en mecûÀnica general por Hamilton como la suma de todas las energûÙas que actû¤an sobre el sistema).
Segû¤n el segundo postulado, estos operadores representan las propiedades correspondientes (posiciû°n y energûÙa) del sistema.
Aplicando (hacer que funcione) el operador de posiciû°n en el estado de la molûˋcula de hidrû°geno tenemos:
P | estado > = | P1 > o P | estado > = | P2 >.
Aplicar el operador sobre el estado significa observar la propiedad correspondiente al operador, aquûÙ la posiciû°n.
De la misma manera con el operador de energûÙa.
H | estado > = | El > o H | estado > = | Enl >.
Podemos ver que cuando aplicamos un operador a un estado, hacemos que este estado evolucione hacia un estado perteneciente a este operador en particular, llamamos a este estado " estado de limpieza" del operador.
El resultado puede ser cualquier estado posible para el sistema y para el operador (la propiedad medida).
El estado " molûˋcula enlazada" es un estado propio del operador de energûÙa mientras que el "electrû°n en el nû¤cleo 1" es un estado propio del operador posiciû°n.
Para la molûˋcula de hidrû°geno en estado ligado, el electrû°n se encuentra en una posiciû°n indeterminada entre los dos nû¤cleos de hidrû°geno.
Se puede decir que el estado propio de energûÙa es una combinaciû°n lineal de estados posicionales, que se puede representar como:
| El > = | P1 > | P2 >
Se puede decir que los dos estados posicionales se suman a un estado energûˋtico: cuando el electrû°n es compartido por los dos nû¤cleos, la molûˋcula estûÀ ligada, se dice que los dos estados posicionales interfieren constructivamente para formar el estado energûˋtico "ligado"..
de la misma manera que el estado no ligado serûÀ representado por | Enl > = | P1 >- | P2 >
se dice que los dos estados posicionales interfieren destructivamente para crear el estado de energûÙa "desligado".
Si retomamos la analogûÙa del pan, el estado de ûÀnimo de la persona es una duda entre ir a comprar el pan al panadero o al pastelero, pero tambiûˋn entre ir a comprar el pan o no comprarlo.
Se puede decir que la determinaciû°n de salir a comprar pan es una interfûˋrence_es de todas las posibilidades para ir a comprar el pan, mientras que la renuncia es una interfûˋrence_es destructiva de estos mismos estados posibles.
Consideramos todas las posibilidades que pueden ocurrirle al sistema y que estûÀn todas incluidas en el espacio de estados.
Geomûˋtricamente se puede representar de la siguiente manera:
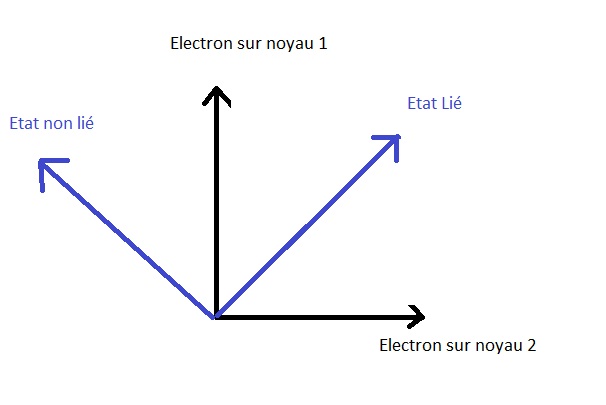
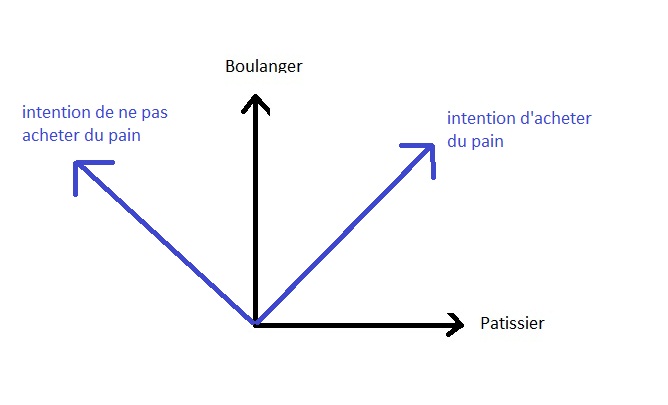 Se puede ver que los estados de energûÙa observables (estados unidos o no unidos de la molûˋcula) tambiûˋn son ortogonales porque corresponden a posibles opciones energûˋticas incompatibles entre sûÙ.
Se puede ver que los estados de energûÙa observables (estados unidos o no unidos de la molûˋcula) tambiûˋn son ortogonales porque corresponden a posibles opciones energûˋticas incompatibles entre sûÙ.
El estado del sistema (vector de estado) es en sûÙ mismo independiente de su representaciû°n en el espacio de estado, ya sea con respecto a la energûÙa o a la posiciû°n.
Se dice que los estados propios asociados a un operador son una base para representar el vector de estado (aquûÙ base azul o negra) AsûÙ, para el vector de estado, tenemos una base de representaciû°n para el operador de posiciû°n y otra base de representaciû°n para el operador de energûÙa.
1.1.2.Principio de incertidumbre de Heisenberg
El principe_d_incertitude_de_Heisenberg se deduce directamente de los postulados de la mecûÀnica cuûÀntica.
Hemos visto que, en general, los estados propios de dos observables no estûÀn representados por los mismos vectores y que un estado energûˋtico, por ejemplo, estarûÀ representado por una combinaciû°n lineal (superposiciû°n) de estados posicionales.
En este caso, estûÀ claro que es imposible observar tanto la propiedad de posiciû°n como la propiedad de energûÙa de un sistema durante la misma mediciû°n, ya que sus estados propios son incompatibles.
MatemûÀticamente decimos que los operadores no cambian.
Esto significa que si los dos operadores se aplican sucesivamente al sistema en un orden diferente, el estado final serûÀ diferente.
En la prûÀctica, en un experimento cuûÀntico, se observa un gran nû¤mero de partûÙculas que da un resultado estadûÙstico global en el que parece que cuanto mûÀs preciso es el valor de la energûÙa, menos precisa es la posiciû°n y viceversa.
1.1.3.Representaciû°n de la funciû°n de onda en el espacio fûÙsico
La diferencia entre el vector de estado y la funciû°n de onda es que el vector de estado es independiente del espacio fûÙsico, mientras que la funciû°n de onda no lo es, porque se propaga en el espacio fûÙsico.
En mecûÀnica cuûÀntica, se dice que la funciû°n de onda es una proyecciû°n del vector de estado en el espacio fûÙsico.
En la imagen siguiente, hemos representado el aspecto de la onda (funciû°n de onda) de los estados cuûÀnticos
visualizar cû°mo la onda interfiere destructiva o constructivamente por adiciû°n o sustracciû°n.
El funcionamiento fundamental de una onda es el mismo tanto si se trata de una onda cuûÀntica como de una
electromagnûˋtica o, por ejemplo, una onda en la superficie de una masa de agua (Vagabundos).
Una onda siempre tiene una oscilaciû°n de valle y de pico (de la onda) en torno a un valor medio (la superficie plana del agua).
Las ventajas se suman (asûÙ como los menos) y los puntos positivos y negativos se restan y anulan entre sûÙ.
Por ejemplo, si la depresiû°n de una onda se encuentra con el pico de otra onda, ambas se anulan mutuamente, dejando
la superficie plana del agua en el punto de superposiciû°n.
1.1.3.1.Estados de las molûˋculas de hidrû°geno
Los estados de onda de un ûÀtomo o molûˋcula corresponden a ondes_stationnaires_es
que son ondas que no se propagan sino que permanecen principalmente localizadas en una regiû°n limitada
del espacio, aquûÙ alrededor de los nû¤cleos de hidrû°geno.

El segundo postulado introduce, pues, los operadores que se aplican a los estados para transformarlos.
Por tanto, podemos decir que el vector de estado representa el aspecto estûÀtico de la realidad cuûÀntica, mientras que el operador representa el aspecto dinûÀmico de esta misma realidad.
Los postulados tercero, cuarto y quinto describen el proceso mismo de observaciû°n de un sistema cuûÀntico.
Postulat_III
Medida : valores posibles de un observable "La mediciû°n de una cantidad fûÙsica A sû°lo puede dar un valor propio del observable A correspondiente entre todos los posibles.
" Hemos visto que los estados observables de una propiedad de un sistema cuûÀntico se llaman "estados propios". (de este observable).
Cada "estado propio" tiene un "valor propio" asociado que es el resultado de la mediciû°n.
Por ejemplo, para la molûˋcula de hidrû°geno serûÀ el nivel de energûÙa de la molûˋcula el que sea diferente si la molûˋcula estûÀ en su estado ligado o no ligado.
En la analogûÙa del pan, se puede imaginar que el resultado es el cambio en la cantidad de dinero en el monedero que ha disminuido cuando se comprû° el pan.
El valor propio es un nû¤mero mientras que el estado propio es, como hemos visto, un vector.
Hasta ahora sû°lo hemos utilizado la direcciû°n del vector, que tambiûˋn estûÀ asociada a una dimensiû°n del espacio de estados, ya que ûˋsta es la nociû°n mûÀs importante relativa al estado cuûÀntico.
En matemûÀticas, el valor natural asociado a un vector es su longitud.
Esta longitud es abstracta (no es un espacio fûÙsico, por lo que no se mide en metros).
Por eso se ha creado un tûˋrmino mûÀs general que hace referencia a la longitud o a la escala, de ahûÙ el nombre de "valor escalar"..
El escalar es, por tanto, el valor numûˋrico asociado a la longitud de un vector.
Si multiplicamos la longitud de un vector por un nû¤mero obtendremos un vector cuya longitud es un mû¤ltiplo del valor inicial, estarûÀ en una escala diferente, su nuevo valor "escalar".
Por lo tanto, aquûÙ estamos observando la energûÙa del sistema utilizando el operador de energûÙa.
Hemos visto que en este caso la aplicaciû°n del operador energûˋtico sobre el estado da los dos posibles estados energûˋticos simultûÀneamente:
H aplicada al | estado > darûÀ el estado | El > (para enlazar) asociado a la energûÙa El es el estado | Enl > (para los no relacionados) asociado a la energûÙa Enl (las energûÙas son los valores propios del operador de energûÙa).
El operador lû°gico "o" (o no exclusiva) se representa en la mecûÀnica cuûÀntica en el espacio de estados mediante la suma de los vectores seûÝalados " ".
Por lo tanto, tenemos:
H | estado > = El | El > Enl | Enl >
El estado global es una superposiciû°n de los posibles estados propios donde El y Enl representan, como hemos visto, los valores energûˋticos de los dos estados respectivamente.
Para representar el hecho de que sû°lo es posible un valor durante una mediciû°n, utilizamos una propiedad de los vectores llamada proyecciû°n.
A continuaciû°n se muestra la imagen de la proyecciû°n global del estado |Psy> en el estado de energûÙa "molûˋcula enlazada" | El >
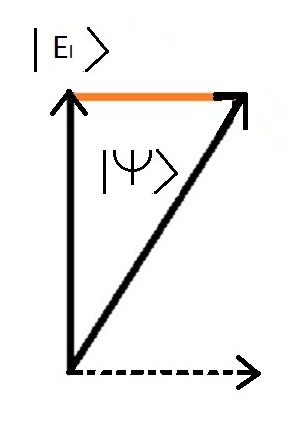 Cuando la propiedad fûÙsica se mide en el sistema, el postulado es que la mediciû°n da un valor û¤nico y que este valor corresponde a un estado particular del sistema llamado "estado propio", denominûÀndose el valor obtenido "valor propio"..
Cuando la propiedad fûÙsica se mide en el sistema, el postulado es que la mediciû°n da un valor û¤nico y que este valor corresponde a un estado particular del sistema llamado "estado propio", denominûÀndose el valor obtenido "valor propio"..
En la ecuaciû°n anterior sumamos posibilidades y no valores, por lo que no tenemos E = El Enl, aûÝadir un vector no funciona como aûÝadir un valor (escalar).
Veremos mûÀs adelante que la suma de posibilidades nos llevarûÀ no a la suma de las energûÙas sino al valor medio de la energûÙa que es la suma de los valores (ici El Enl) dividido por el nû¤mero de valores aûÝadidos (ici 2).
Por lo tanto, el valor energûˋtico medio serûÙa E = (El Enl)/2.
En realidad es un poco mûÀs sutil que eso porque el valor medio de la energûÙa tambiûˋn depende de la probabilidad de existencia de cada estado de energûÙa, por lo que es un valor medio ponderado por la probabilidad de cada estado.
Este es precisamente el tema del cuarto postulado.
Postulat_IV
Postulado de nacimiento : interpretaciû°n probabilûÙstica de la funciû°n de onda "Al medir la cantidad fûÙsica A en un sistema en el estado normalizado "phi", la probabilidad P (Un) para obtener el valor propio An del observable correspondiente A es |Cn|ôý.
Donde Cn es la amplitud de la funciû°n de onda proyectada sobre el estado propio |phi n> correspondiente al valor propio observado An.
Hasta ahora sû°lo hemos hablado de estados, estados propios observables y sus valores propios asociados.
Por convenciû°n, la longitud de cualquier vector de estado es 1, la razû°n es que el vector de estado transmite la existencia del sistema (primer supuesto) y que en tûˋrminos de probabilidad, la afirmaciû°n de la existencia del sistema corresponde a una certeza.
En probabilidad la certeza es 1.
Cuando tienes una probabilidad de 1 en 1 de cualquier cosa (1 dividido por 1 es igual a 1) estamos en la certeza.
Una probabilidad inferior a 1 es menos segura que la certeza total.
Por ejemplo, la probabilidad de ganar la loterûÙa jugando sû°lo a una cuadrûÙcula es de 1 dividido por unos cuantos millones.
Esto significa que al final sû°lo uno o casi uno ganarûÀ los millones del sorteo ! El sorteo en tûˋrminos cuûÀnticos es " la observaciû°n del ganador".
La amplitud de la funciû°n de onda es la misma que la longitud del vector de estado.
Hemos visto que un escalar es un valor numûˋrico simple.
Esta denominaciû°n tambiûˋn aparece en comparaciû°n con valores numûˋricos mûÀs complejos compuestos por varios nû¤meros, como el vector que, al representarse numûˋricamente, requiere el uso de varios nû¤meros.
(si seguimos esta lûÙnea de desarrollo llegamos al concepto de "tensor" muy utilizado en fûÙsica, tensor de elasticidad, de curvatura del espacio-tiempo...Postulado IV nweb).
_
Cuando un vector se proyecta sobre otro, la longitud transportada del primero al segundo es un nû¤mero.
Hemos realizado asûÙ una operaciû°n que asocia un nû¤mero a dos vectores, que llamamos escalar para indicar que el resultado particular de esta operaciû°n de dos vectores no da un tercer vector como en la suma de vectores sino un nû¤mero (escalar).
Esta operaciû°n se denomina producto escalar: El producto escalar es una operaciû°n que, a partir de dos vectores, da un nû¤mero.
Este nû¤mero es la longitud proyectada ortogonalmente de un vector sobre el otro.
La palabra inglesa "bracket" se refiere a los caracteres "<" et ">" Estos parûˋntesis se utilizan tradicionalmente en matemûÀticas para representar el valor medio de una cantidad. La imagen siguiente representa la proyecciû°n del estado general | Perros > en los dos estados de energûÙa | Perros l > y | Perros nl > (que son los mismos que los estados | El > y | Enl > es sû°lo una diferencia de notaciû°n)
Cuando consideramos los estados "compra de pan" |panadero> y |panadero> consideramos implûÙcitamente que podemos observar uno y otro de forma indiferente, es decir, con igual probabilidad de ocurrencia.
" La suma del cuadrado de las longitudes de los dos lados es igual al cuadrado de la longitud de la hipotenusa" En nuestro caso la hipotenusa corresponde al vector estado |phi> y ambos lados a la |phi> en los dos estados propios |panadero> y | Epicier>. Si consideramos la expresiû°n | Perros L >< Perros L | compuesto por un ket y un sujetador y aplicado al ket | Perros > obtenemos | Perros L >< Perros L | Perros > donde < Perros L | Perros > es la amplitud de la probabilidad de obtener el estado | Perros L > por lo que tenemos : | Perros L >< Perros L | Perros > = | Perros L > Al = Al | Perros L > vemos que el estado final es el | Perros L > asociado a la probabilidad Al La expresiû°n | Perros L >< Perros L | es por tanto un operador que ha cambiado el estado inicial | Perros > al estado final | Perros L > y esto con una probabilidad Al.
1.2.2.Particiû°n del operador de la unidad
Considere el siguiente operador:
| Perros L >< Perros L | | Perros nl >< Perros nl | que es la suma de los operadores de evoluciû°n hacia los estados propios de un observable (aquûÙ la energûÙa : estado ligado y no ligado).
Es interesante observar cû°mo la representaciû°n vectorial del estado y su descomposiciû°n segû¤n una base ortogonal permite representar de forma natural las amplitudes de las probabilidades y, por tanto, las probabilidades de la evoluciû°n del sistema durante una mediciû°n.
Postulat_V
Medida : reducciû°n de paquetes de ondas Si la mediciû°n de la cantidad fûÙsica A, en el tiempo t, en un sistema representado por el vector |phi> da como resultado el valor propio An, entonces el estado del sistema inmediatamente despuûˋs de la mediciû°n se proyecta en el espacio propio asociado a An Este postulado tambiûˋn se llama " postulado de reducciû°n de paquetes de ondas".
Es probablemente la mayor revoluciû°n conceptual de la mecûÀnica cuûÀntica introducir el hecho de que la observaciû°n del sistema lo hace evolucionar, mientras que en las teorûÙas fûÙsicas no cuûÀnticas es sû°lo la ecuaciû°n dinûÀmica la responsable de la evoluciû°n del sistema.
Tradicionalmente la ecuaciû°n dinûÀmica de una teorûÙa mecûÀnica expresa cû°mo la energûÙa actû¤a sobre el sistema para transformarlo.
L_expûˋrience_du_chat_de_Shroedinger es un experimento mental ideado por el fûÙsico Erwin_Shroedinger reflexionar sobre el problema de la mediciû°n en la mecûÀnica cuûÀntica directamente relacionado con el quinto postulado.
Obsûˋrvese el vûÙnculo entre el observador y la funciû°n de onda: ninguno de los cuales es material ! Se podrûÙa decir que lo material es lo que estûÀ entre los dos: observaciû°n.
La funciû°n de onda y la conciencia representan dos caras de una misma realidad que trasciende la materialidad y
en el origen mismo de esta materialidad.
Obviamente, los fûÙsicos en su conjunto no suelen ir tan lejos en su visiû°n de la realidad cuûÀntica.
La posiciû°n estûÀndar en esta zona es lainterprûˋtation_de_l_ûˋcole_de_Copenhague.
Esta posiciû°n surge de la situaciû°n del observador humano que experimenta un mundo clûÀsico y lo considera como la referencia absoluta.
Se pueden definir diferentes grados de distancia con respecto a esta posiciû°n:
Cabe seûÝalar que este punto de vista ya no es cientûÙficamente sostenible desde el experimento de Aspect, que valida la mecûÀnica
en sus declaraciones mûÀs inquietantes.
Al mismo tiempo, esta mecûÀnica cuûÀntica es la teorûÙa mûÀs verificada en la historia de la ciencia.
Este punto de vista se reduce asûÙ a una simple creencia "materialista..
Sin embargo, esta era la opiniû°n de Einstein, pero desgraciadamente no viviû° lo suficiente para
ver la resoluciû°n mediante el experimento Aspect de la paradoja que definiû° con los fûÙsicos Podolsky y Rosen en su famoso artûÙculo:
el Paradoxe_EPR.
AquûÙ el mundo clûÀsico en el que vivimos ya no representa la totalidad del mundo porque hay
un mundo cuûÀntico absolutamente extraûÝo al que no tenemos acceso pero con el que podemos tratar por
a travûˋs de la teorûÙa cuûÀntica.
El mundo fûÙsico estable que conocemos estûÀ formado por sû°lo tres partûÙculas cuûÀnticas: electrû°n, protû°n y neutrino.
Este tercer punto de vista elimina todas las paradojas cuûÀnticas al decir, final y simplemente, que no debemos
no buscar una interpretaciû°n (clûÀsico) de la teorûÙa cuûÀntica, sino que simplemente hay que aceptarla
como es (Copenhague) y finalmente reconocer la supremacûÙa de su posiciû°n.
Por lo tanto, se puede predecir que el modelo cuûÀntico nunca serûÀ fallado. Desde su creaciû°n, cada vez estûÀ mûÀs claro cû°mo la realidad cuûÀntica
interviene en la comprensiû°n del mundo que nos rodea y mûÀs concretamente en el ûÀmbito de la vida, un sistema macroscû°pico de gran coherencia... quantum.
Dos ejemplos bastante recientes son:
Postulat_VI evoluciû°n temporal del estado cuûÀntico. _ H |Phi(t)> = i h/2*pi d |Phi(t)> / dt _
0,000000000000000000000000000000000662607004 Cuando esta constante se combina con otras constantes fundamentales como la velocidad de la luz o la constante gravitatoria universal, se pueden deducir las cantidades mûÙnimas de las diferentes unidades de la fûÙsica : Longitud de Planck, tiempo de Planck, etc....
1.5.Expresiû°n poûˋtica condensada de los postulados
A continuaciû°n se trata de combinar todos los supuestos en un solo aforismo:
" Lo que es posible se cumple, bajo la mirada de la conciencia, sû°lo se cumple lo que es posible.
La mecûÀnica cuûÀntica es la mayor revoluciû°n de nuestra era cientûÙfica moderna porque destruye definitivamente la posiciû°n materialista, abriendo asûÙ el camino a un desarrollo de la humanidad donde la ciencia y la conciencia volverûÀn a estar unidas.
2.Aspecto de alain en toulouse
El experimento decisivo que zanjû° la parodia Einstein-Podolski-Rosen
realizada en 1982 por Alain Aspect, investigador y experimentador del centro de û°ptica cuûÀntica de Orsay
se basû° en los fotones.
Una descripciû°n detallada de la teorûÙa subyacente puede encontrarse en el libro
de Bernard d'Espagnat "A la bû¤squeda del real".
Ese mismo aûÝo, yo estaba en la universidad y Alain Aspect vino a presentar
sus resultados en Toulouse, en el anfiteatro Maxwell de la Universidad Paul Sabatier.
Tras presentar los resultados inequûÙvocos de las mediciones, dejû°
la asamblea sin voz (la sala de conferencias estaba llena de profesores e investigadores).
Al final de la presentaciû°n, tras un significativo momento de silencio, cuando se abriû° el turno de palabra, el orador dijo
se entregû° a la asamblea, sû°lo un investigador se levantû° (mi profesor de relatividad) y se hizo esta pregunta:
ô¢Y te resulta fûÀcil vivir con eso ahora?.
Aspecto, a la defensiva, respondiû° que no habûÙa dicho eso, que habûÙa hecho
un experimento y que el resultado fue ese, pero que tuvo cuidado de no
dar cualquier interpretaciû°n.
AûÝos mûÀs tarde supe por alguien que habûÙa estado con ûˋl que era
pro-einsteiniano y que esperaba que la mecûÀnica cuûÀntica fuera cuestionada.
Yo estaba en la bahûÙa lateral en la tercera fila, solo y me divertûÙa porque no entendûÙa
por quûˋ tenûÙan un problema con ûˋl, o mûÀs bien lo entendûÙ muy bien.
Cuando el experimento estaba en sus inicios, pero el resultado era sû°lo cuestiû°n de tiempo,
la controversia se ha vuelto muy fuerte, incluso sulfurosa.
Cuando la comunidad cientûÙfica de fûÙsicos estaba en shock, nosotros
podûÙa preguntarse quûˋ iba a pasar.
Se necesitû° tiempo para digerir la informaciû°n, podemos ver en 2020 que la situaciû°n
ha evolucionado bastante, sû°lo hay que ver esta conferencia impartida en la Escuela Politûˋcnica
por Hervûˋ Zwirn, Director de Investigaciû°n del CNRS
_x_sciences_de_l_homme_et_de_la_sociûˋtûˋ_x_shs_mûˋcanique_quantique_le_monde_existe_t_il
Esta experiencia ha tenido (o deberûÙa haber tenido para la mayorûÙa) el mismo tipo de efecto en el
fûÙsicos que el descubrimiento de las ondas de radio (ondas electromagnûˋticas) que tienen
dar al concepto abstracto del campo electromagnûˋtico una realidad mucho mûÀs viva.
El descubrimiento de la no separabilidad y su observaciû°n en el
nivel fûÙsico da vida al concepto de realidad independiente, es decir
de una realidad independiente del espacio y del tiempo, es decir, de toda
contingencias espacio-temporales, es decir, todas las contingencias fûÙsicas.
Una primera conclusiû°n que se puede extraer del primer postulado de la mecûÀnica
es que:
La realidad de un sistema cuûÀntico (y al final, todos los sistemas son cuûÀnticos! x ciencias humanas y sociales x shs mecûÀnica cuûÀntica existe el mundo nwebs) se apoya en
por un espacio abstracto de posibilidades que es inobservable en sûÙ mismo (no fûÙsica y
independiente de todas las contingencias espaciales y temporales) pero sin embargo real, ya que es
de este nivel abstracto de funcionamiento surge la realidad concreta (observado).
Para resumirlo en una palabra: es omnipresencia y omnisciencia ya que contiene
toda la informaciû°n sobre el sistema fûÙsico de forma no local.
AdemûÀs, para ser completos, esto estûÀ relacionado con el observador, que obviamente no puede ser fûÙsico.
Queda claro que el observador y la realidad independiente tienen una estrecha relaciû°n:
ambos son no fûÙsicos e interactû¤an en tûˋrminos de informaciû°n, conocimiento, percepciû°n.
En este sentido, la pelûÙcula Matrix puede verse como una alegorûÙa de la realidad cuûÀntica.
Esta conciencia universal puede recibir y ha recibido el nombre que se quiera
pero estos nunca agotarûÀn el poder infinito de esta conciencia.
El valor medio de la energûÙa se anotarûÀ, por ejemplo < E >.
Hemos visto que el estado cuûÀntico tambiûˋn se llama "ket" anotado | ket > la otra parte del parûˋntesis es el "bra" que es un operador particular seûÝalado < sujetador | Es el fûÙsico Paul_Dirac que estûÀ en el origen de esta separaciû°n en dos de esta palabra para hacer aparecer una dinûÀmica de operador y vector en la operaciû°n de tomar el valor medio.
Si aplicamos la "bra" al "ket" obtenemos < sujetador | ket > que es el nû¤mero que resulta de aplicar el operador
AquûÙ tenemos una doble relaciû°n entre el sujetador y el ket.
Para un estado (ou ket) "| Perros >^ le bra sera "< Perros |" la dualidad entre los dos se representa como la imagen en un espejo El ket es un vector mientras que el bra es un operador, aplicando el bra al ket se obtiene un nû¤mero.
En general, en una expresiû°n lo que estûÀ a la derecha del ket es un operador, el resultado de un operador sobre un estado (vector) es otro estado (vector) un nû¤mero que representa el resultado de una mediciû°n o una probabilidad.
Para cada ket hay un bra correspondiente y la operaciû°n que permite pasar del ket al bra se llama conjugaciû°n hermûˋtica y se seûÝala con una estrella.
AsûÙ, ( | Perros > ) * = < Perros | o (
Esto puede relacionarse anûÀlogamente con un aforismo vûˋdico en el que el creador del universo habla: " girando sobre mûÙ mismo, creo una y otra vez".
La misma forma puede verse tambiûˋn en el primer relato de la creaciû°n en el Gûˋnesis: que se haga la luz y se haga la luz y D.
Dios vio que la luz era buena.
< que se haga la luz | y la luz era > = y D.
Dios vio que la luz era buena.
< o | luzôý. | barril > = D.
Dios vio que la luz era buena.
El hecho de que D.
Dios vio que la luz era buena es claramente el resultado de una observaciû°n.
PodrûÙamos llamar a todo esto el alfabeto cuûÀntico y la sintaxis.
El alfabeto consta de una sola letra | Perros > y eso es " el ser" (o el estado que es la afirmaciû°n del ser) La operaciû°n dual * muestra su valor de operador dinûÀmico ( | Perros > )* = < Perros | Todas sus combinaciones dan lugar a la gramûÀtica cuûÀntica.
Un ejemplo es la aplicaciû°n del operador < Perros | sobre el estado | Perros > da < Psy|Perros > que tambiûˋn es la proyecciû°n del |Psy> sobre sûÙ mismo y, por tanto, es 1.
Esto se puede traducir trivialmente en la siguiente frase: "Psy participa al 100%. (100/100=1) a Psy".
< Perros L | Perros > es la proyecciû°n del estado general del sistema sobre el estado de energûÙa lûÙmite de la molûˋcula de H2 ejemplo y representa la amplitud de probabilidad de obtener el estado lûÙmite durante una observaciû°n.
Al = < Perros L | Perros > Tomando el cuadrado de la amplitud se obtiene la probabilidad La probabilidad del estado | Perros L > es: Pl = Alôý = ( < Perros L | Perros > )ôý 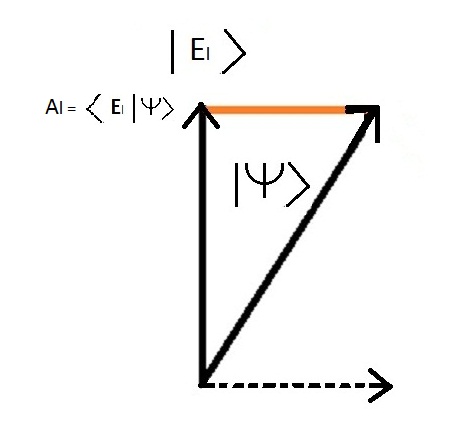
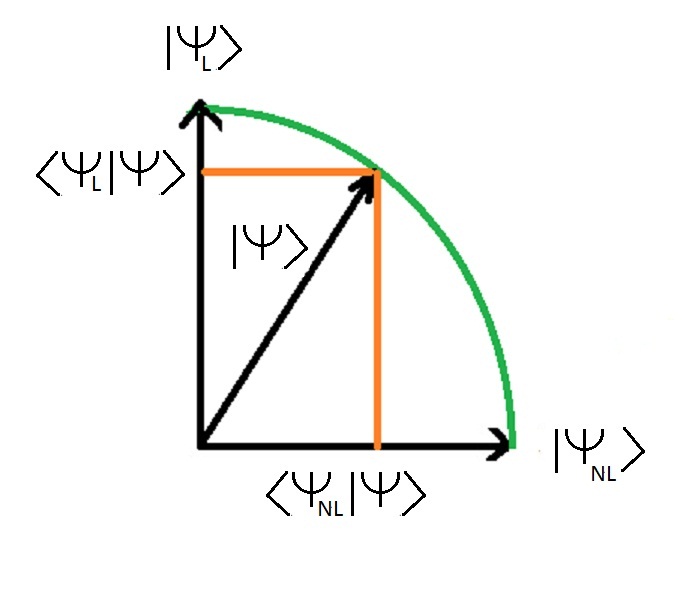 Los dos valores < Perros l | Perros > y < Perros nl | Perros > son la longitud del estado | Perros > (que es 1) proyectado en las propias declaraciones | Perros l > y | Perros nl > < Perros l | Perros > es la proyecciû°n del estado | Perros > sobre el estado de limpieza | Perros l > < Perros nl | Perros > es la proyecciû°n del estado | Perros > sobre el estado de limpieza | Perros nl >
Los dos valores < Perros l | Perros > y < Perros nl | Perros > son la longitud del estado | Perros > (que es 1) proyectado en las propias declaraciones | Perros l > y | Perros nl > < Perros l | Perros > es la proyecciû°n del estado | Perros > sobre el estado de limpieza | Perros l > < Perros nl | Perros > es la proyecciû°n del estado | Perros > sobre el estado de limpieza | Perros nl >
Esto se conoce como un estado equiprobable.
Pero las caracterûÙsticas del sistema pueden ser tales que no sea asûÙ, por ejemplo, si el panadero estûÀ mûÀs cerca de casa que el pastelero y hace mucho frûÙo la probabilidad del estado |panadero> serûÀ mûÀs fuerte que la del Estado |panadero>.
Esto se representa en la imagen siguiente, donde Ab es mayor que Ap.
(A es la amplitud de la probabilidad).
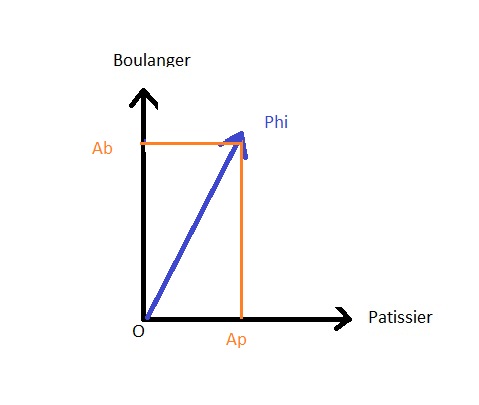 La proyecciû°n del estado |Phi> general sobre el estado |panadero> tiene el valor Ab que corresponde a la amplitud de probabilidad de obtener este estado a partir del estado general |Phi> Lo mismo ocurre con Ap, que es la amplitud de la probabilidad de obtener el estado |panadero>.
La proyecciû°n del estado |Phi> general sobre el estado |panadero> tiene el valor Ab que corresponde a la amplitud de probabilidad de obtener este estado a partir del estado general |Phi> Lo mismo ocurre con Ap, que es la amplitud de la probabilidad de obtener el estado |panadero>.
Los estados propios cuûÀnticos son siempre ortogonales, es decir, se encuentran en ûÀngulo recto entre sûÙ y, por tanto, siguen la . Pythagore
para el triûÀngulo rectûÀngulo.
El postulado dice que el cuadrado de la amplitud de la onda es la probabilidad.
Considerar el estado general del sistema significa simplemente considerar que hay: la probabilidad del estado real del sistema es, por tanto, siempre igual a 1.
Esto es lo que menciona el postulado al decir que el estado |phi> es normado y su norma es siempre igual a 1 por convenciû°n ya que es una probabilidad.
MatemûÀticamente observamos < phi | phi > = 1 = | |phi> | ôý (la û¤ltima expresiû°n representa el cuadrado de la norma del vector, siendo la norma del vector su longitud) A continuaciû°n, esta probabilidad se divide en varias probabilidades inferiores correspondientes a cada estado propio, pero con la restricciû°n de que la suma de los cuadrados de las amplitudes de los estados propios del sistema sea siempre igual a 1, que es la probabilidad cierta.
En nuestro caso tenemos:
Abôý Apôý = 1 La suma de las probabilidades de todos los estados posibles del sistema debe ser igual a 1.
Se puede decir que la existencia del sistema se extiende sobre todas sus posibilidades de existencia pero sin ninguna pûˋrdida de existencia por lo que su existencia se conserva.
En efecto, si la probabilidad total disminuyera, esto significarûÙa que el sistema tendrûÙa menos posibilidades de existir y al reducir la probabilidad de su existencia a cero, desaparecerûÙa ! La amplitud del estado o de la funciû°n de onda puede ser positiva o negativa, al igual que el pico o la depresiû°n de una onda.
La amplitud de la probabilidad es, por tanto, negativa o positiva, que es lo que hemos representado en la imagen de los estados ligados y no ligados de la molûˋcula de hidrû°geno mediante los sûÙmbolos mûÀs y menos - .
(. ûˋtats molûˋcule hydrogû´ne PitûÀgoras) Pero la probabilidad que es el cuadrado de la amplitud (o el cuadrado de la norma ) es por lo tanto siempre positivo, lo que es normal para una probabilidad.
En efecto, podemos imaginar una probabilidad cierta, luego una menos cierta, luego una incierta o incluso una nula, pero una probabilidad negativa no tiene sentido.
Por otro lado, la amplitud de la probabilidad puede ser negativa.
Supongamos entonces que tenemos dos amplitudes de probabilidad iguales pero de signos opuestos que se propagan la una hacia la otra (son ondas).
Si consideramos las probabilidades cuando estas amplitudes estûÀn en el mismo lugar, entonces las amplitudes de signos opuestos se anulan y su cuadrado tambiûˋn es cero.
La probabilidad de observar algo serûÀ cero.
Pero si las amplitudes estûÀn separadas su cuadrado serûÀ positivo (mûÀs por mûÀs es positivo, pero menos por menos tambiûˋn lo es) y por lo tanto la probabilidad de observar algo ya no serûÀ cero.
Cuando hablamos de la mecûÀnica cuûÀntica pensamos en su carûÀcter probabilûÙstico como un juego de azar, pero lo que generalmente ignoramos es que estas probabilidades se sustentan en algo mucho mûÀs inquietante, que es la amplitud de la onda de probabilidad y que da a la mecûÀnica cuûÀntica su realidad.
Es un operador de evoluciû°n que ha hecho que el sistema evolucione al estado de energûÙa lûÙmite durante una observaciû°n.
Esto nos lleva naturalmente al quinto postulado que describe cû°mo evoluciona el sistema durante una mediciû°n.
Si aplicamos este operador a ket | Perros > en un :
( | Perros L >< Perros L | | Perros nl >< Perros nl | ) | Perros > o | Perros L >< Perros L | Perros > | Perros nl >< Perros nl | Perros > lo que resulta en | Perros L > Al | Perros nl > Anl o incluso Al | Perros L > Anl | Perros nl > que es la descomposiciû°n del estado | Perros > en la suma de sus propios estados energûˋticos | Perros > = Al | Perros L > Anl | Perros nl > El operador no ha cambiado el estado | Perros > sino que simplemente lo ha descompuesto en sus partes individuales, por esta razû°n se denomina operador de particiû°n "unitaria"..
En primer lugar, vamos a dilucidar esta nociû°n de "sub-eigenspace".
Es sû°lo una generalizaciû°n de la descomposiciû°n del estado en sus estados propios.
Volvamos al ejemplo del pan con dos panaderos y un pastelero.
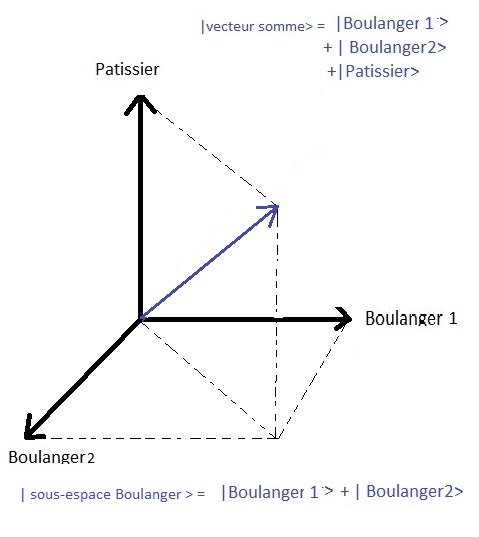
Si la distinciû°n del tipo de comercio no es observable (no es un observable del sistema)En el caso de una mediciû°n, no serûÀ necesario distinguir si se trata del panadero 1 o del panadero 2, bastarûÀ con saber que el estado ha sido proyectado al subespacio propio del panadero, que de hecho corresponde, en el diagrama siguiente, al plano horizontal poblado por los panaderos ! Si existiera un observable que permitiera observar a quûˋ panadero se comprû° el pan, durante esta mediciû°n el estado se proyectarûÙa a uno u otro de los panaderos, levantando la indeterminaciû°n de la mediciû°n.
Pero si esta propiedad del sistema no se observa entonces el sistema permanece en este estado de superposiciû°n de las funciones de onda de Baker.
Se dice que el estado es degenerado.
En la prûÀctica, cuando varios estados propios tienen el mismo valor propio (la misma energûÙa) han dicho que estos estados son degenerados.
Aplicando una restricciû°n energûˋtica adicional al sistema que cambiarûÀ la energûÙa de los estados degenerados para que ya no haya igualdad, se eliminarûÀ la degeneraciû°n.
La fûÙsica cuûÀntica se ocupa esencialmente de comprender la estructura del mundo microscû°pico, que se compone esencialmente de resonancias (ondas estacionarias) que son estados propios del operador de energûÙa total del sistema (Hamiltonien).
 El quinto postulado establece que durante la mediciû°n, el estado del sistema evoluciona hacia el estado cuyo valor propio ha sido medido.
El quinto postulado establece que durante la mediciû°n, el estado del sistema evoluciona hacia el estado cuyo valor propio ha sido medido.
Es este llamado postulado de "reducciû°n de paquetes de onda" o "colapso de la funciû°n de onda" el que da a la representaciû°n geomûˋtrica de una proyecciû°n vectorial su realidad fûÙsica, ya que el sistema evoluciona fûÙsicamente en esta operaciû°n.
En este quinto postulado hemos visto que la propia mediciû°n transforma el sistema.
En el caso de la mecûÀnica cuûÀntica tambiûˋn existe una ecuaciû°n dinûÀmica de este tipo y se denomina la ecuaciû°n de Shroedinger .
En la mecûÀnica, existen por tanto dos mecanismos de evoluciû°n: la acciû°n de la energûÙa en el tiempo y la acciû°n de la observaciû°n fuera del tiempo.
Esta ecuaciû°n constituye el sexto y û¤ltimo postulado de la mecûÀnica cuûÀntica (ver mûÀs abajo).
El quinto postulado implica al observador del sistema en la evoluciû°n del mismo.
AsûÙ, en la mecûÀnica cuûÀntica el observador ya no es independiente del sistema fûÙsico.
El observador y el sistema fûÙsico forman un conjunto inseparable.
Se podrûÙa decir que el observador estûÀ integrado en el sistema (pero no en el sentido del entrelazamiento cuûÀntico, que sû°lo se refiere a la funciû°n de onda).
Ya hemos mencionado el fenû°meno del entrelazamiento cuûÀntico, que surge del hecho de que un sistema cuûÀntico formado por varias partûÙculas se describe mediante una û¤nica funciû°n de onda (primer supuesto) aunque es probable que las partûÙculas se hayan alejado en el espacio fûÙsico.
Segû¤n el quinto postulado, durante una mediciû°n la funciû°n de onda colapsa en un subespacio propio afectando al mismo tiempo al estado de todas las partûÙculas que componen el sistema.
Fue esta implicaciû°n de la mecûÀnica cuûÀntica la que Einstein oficialmente nunca pudo admitir porque, en su opiniû°n, violaba el lûÙmite de propagaciû°n de cualquier interacciû°n fûÙsica definida por la velocidad de la luz.
Segû¤n la teorûÙa de la relatividad de Einstein ninguna energûÙa puede viajar mûÀs rûÀpido que la velocidad de la luz.
La luz, obviamente, viaja a la velocidad de la luz y sû°lo puede hacerlo porque es energûÙa pura, es decir, sin masa.
Por lo tanto, las partûÙculas de masa deben moverse necesariamente a una velocidad inferior a la de la luz.
La resoluciû°n "fûÙsica" de esta paradoja cuûÀntica se llevû° a cabo mediante un experimento conocido como elexpûˋrience_d_Aspect.
Este experimento demostrû° indiscutiblemente que la funciû°n de onda no depende del espacio fûÙsico en el que vivimos: su evoluciû°n durante el colapso debido a la observaciû°n tiene lugar en cualquier punto del espacio al mismo tiempo.
El experimento de Aspect ha sido replicado muchas veces en condiciones cada vez mûÀs sofisticadas para llevar la mecûÀnica cuûÀntica a sus lûÙmites, pero nunca ha cedido ! Se dice que la teorûÙa cuûÀntica es una teorûÙa no local.
Los tûˋrminos utilizados "no localidad" o "no separabilidad" son equivalentes.
Por tanto, podemos decir que la funciû°n de onda cuûÀntica trasciende el espacio fûÙsico, incluso trasciende el espacio-tiempo ya que desde la teorûÙa de la relatividad de Einstein debemos considerar el espacio y el tiempo como aspectos de una misma realidad mûÀs profunda : el continuo espacio-tiempo.
Un experimento mûÀs reciente llevado a cabo en un marco relativista y siguiendo el experimento de Aspect ha confirmado la validez del entrelazamiento cuûÀntico en el marco relativista.
( Vûˋase Expûˋrience_d_Antoine_Suarez que se encuentra en el sitio web del fûÙsico Philippe_Guillemant que ofrece una visiû°n que integra la realidad cuûÀntica ) Este û¤ltimo experimento es importante porque en un experimento de fûÙsica sû°lo se pueden medir valores dentro de un rango determinado.
AsûÙ, en el primer experimento de Aspect, los detectores de fotones correlacionados (en un û¤nico estado cuûÀntico) estaban a pocos metros de distancia.
Esto fue suficiente para demostrar que el entrelazamiento cuûÀntico no podûÙa deberse a un fenû°meno fûÙsico desconocido (variable oculta) a una velocidad sub-lumûÙnica.
La velocidad de tal fenû°meno serûÙa necesariamente superlumûÙnica.
Aunque tal velocidad superlumûÙnica es difûÙcilmente aceptable debido a la teorûÙa de la relatividad de Einstein, el primer experimento de Aspect no descartû° completamente esta posibilidad.
Con el experimento de Antoine SuûÀrez esto se hace porque incluso se suprime la posibilidad de una causalidad entre las detecciones de los dos fotones correlacionados, porque los marcos de referencia relativistas en los que se realizan las detecciones, no permiten un "antes" y un "despuûˋs", condiciû°n esencial para la causalidad: ningû¤n fotû°n se detecta antes o despuûˋs del otro porque estas detecciones no se realizan en los mismos marcos temporales.
En una teorûÙa cuûÀntica relativista la funciû°n de onda ya no puede depender del tiempo como hemos visto en el primer postulado.
La razû°n es que el tiempo se reduce al mismo nivel que la posiciû°n, es decir, una propiedad observable del sistema, y la funciû°n de onda es independiente de las propiedades del sistema (segunda premisa).
En dicha teorûÙa la funciû°n de onda serûÙa | Perros > y ya no | Psy(t) > .
El tiempo serûÙa un observable T del mismo modo que la posiciû°n P.
La particularidad de este experimento mental completamente irreal presentado con un gato " real es hacer pensar en quûˋ es el observador en la mecûÀnica cuûÀntica.
Has visto en los postulados sobre la medida (o la observaciû°n) que no entremos en detalles sobre lo que es el observador.
Los postulados dicen que hay un observador que hace la mediciû°n pero no dicen nada mûÀs sobre la naturaleza del observador ! En este experimento, se aûÙsla a un gato en una caja para que no pueda ser observado (cuantificado) de cualquier manera.
Esto supone que el gato puede ser considerado como un objeto cuûÀntico, lo que no es el caso en la prûÀctica, aunque en teorûÙa el gato puede ser considerado a priori como un sistema fûÙsico, al estar compuesto por ûÀtomos que son y estûÀn bien descritos por la mecûÀnica cuûÀntica.
En esta cûÀmara tambiûˋn hay una ampolla que contiene un gas mortal para el gato y un detector de partûÙculas que abre la ampolla si se detecta una partûÙcula.
Si se detecta una partûÙcula el gato estarûÀ muerto, si no se detecta el gato estarûÀ vivo.
Mientras no hayamos observado el estado de salud del gato "cuûÀntico" permanece en un estado cuûÀntico general conocido como superposiciû°n de estados propios observables, que son | gato vivo > y | chat mort > por lo que tenemos | chat > = | gato vivo > | chat mort > Nuestro sistema cuûÀntico estûÀ formado por varios componentes: el gato, el detector, la partûÙcula.
Todos estos subsistemas tambiûˋn deben ser considerados en el establecimiento de la funciû°n de onda, por lo que tenemos: | partûÙcula > = | partûÙcula presente > | partûÙcula ausente > y | sensor > = | partûÙcula de estado detectada > | estado de la partûÙcula no detectada > Las matemûÀticas asociadas a la mecûÀnica cuûÀntica muestran que el sistema global que llamaremos "shroedinger" es : | shroedinger > = | gato, detector, partûÙcula > = | chat> ôÊ | sensor > ôÊ | partûÙcula > donde ôÊ es el "producto tensorial" de los vectores de estado.
Al encontrarse en el mismo estado cuûÀntico, se dice que estos diferentes subsistemas estûÀn intrincados.
Este producto se comporta como una transacciû°n de producto normal, es distributivo : A * ( B C ) = A*B A*C En tûˋrminos cuûÀnticos podemos por tanto desarrollar el estado cuûÀntico general.
Empecemos con el sistema formado û¤nicamente por el detector y la partûÙcula.
| detector de partûÙculas > = | sensor > ôÊ | partûÙcula > = ( | partûÙcula de estado detectada > | estado de la partûÙcula no detectada > ) ôÊ ( | partûÙcula presente > | partûÙcula ausente > ) mediante el desarrollo de :
| detector de partûÙculas > = | partûÙcula de estado detectada > ôÊ | partûÙcula presente >
| estado de la partûÙcula no detectada > ôÊ | partûÙcula ausente >
| estado de la partûÙcula no detectada > ôÊ | partûÙcula presente >
| partûÙcula de estado detectada > ôÊ | partûÙcula ausente >
Erwin Shroedinger nweb Los dos primeros estados se entienden fûÀcilmente, si la partûÙcula estûÀ presente es lû°gico que se detecte y si no estûÀ presente no se detecta.
Los dos estados siguientes son altamente improbables, pero sin embargo existen segû¤n la mecûÀnica cuûÀntica, para la que todo es sû°lo una amplitud de probabilidad.
Para el Estado | shroedinger > completa serûÙa necesario desarrollar mûÀs con los estados del gato, lo que nos llevarûÙa a una funciû°n de onda con ocho posibles estados propios, dos de los cuales son altamente probables y seis altamente improbables.
Los dos estados probables son:
| chat mort > ôÊ | partûÙcula de estado detectada > ôÊ | partûÙcula presente > | gato vivo > ôÊ | estado de la partûÙcula no detectada > ôÊ | partûÙcula ausente > Mientras no hayamos observado el sistema, lo que corresponde por ejemplo a la apertura de la caja, estamos en un estado de superposiciû°n en el que el gato se encuentra en un estado vital indeterminado.
AquûÙ radica la paradoja.
Pero podemos llevar el razonamiento mûÀs allûÀ y esto es lo que hizo el fûÙsico Eugû´ne_Wigner Premio Nobel de FûÙsica.
Esta es la thûˋorie_de_l_influence_de_la_conscience Considerû° que el ojo del observador que ve al gato vivo o muerto es tambiûˋn un sistema cuûÀntico con dos estados: | oeil > = | el ojo ve el gato muerto > | el ojo ve al gato vivo > Los estados de la funciû°n de onda completa tendrûÙan entonces en cuenta estados "alucinatorios" donde el ojo verûÙa muerto, el gato vivo...
Pero podrûÙamos seguir considerando la cadena de mediciû°n hasta el cerebro del observador, que tambiûˋn estûÀ compuesto de ûÀtomos.
AsûÙ que la pregunta es : cuando se realiza realmente la mediciû°n, es decir, el colapso de la funciû°n de onda y, por tanto, la elecciû°n del resultado del experimento: gato vivo o muerto.
Wigner dice que nada material puede causar el colapso porque toda la materialidad es susceptible de ser descrita por la mecûÀnica cuûÀntica y por lo tanto forma parte de la funciû°n de onda y tambiûˋn se puede considerar muy bien la funciû°n de onda del universo.
Si nada material opera la mediciû°n, sû°lo queda algo inmaterial que lo hace, y esto Wigner lo identifica con la conciencia, que finalmente identifica lo que es el observador.
En su interpretaciû°n El observador es la conciencia .
Esto nos acerca a la concepciû°n de "realidad independiente" o "realidad velada" introducida por el fûÙsico Bernard_d_Espagnat para la comprensiû°n filosû°fica de la mecûÀnica cuûÀntica.
bernard_d_espagnat_physique_quantique_et_rûˋalitûˋ_la_rûˋalitûˋ_c_est_quoi ;Obtenido de \" https://www.
youtube.
com/watch?v=Jd8FiWJ5v8M; Esto tambiûˋn nos acerca a la concepciû°n vûˋdica en la antigua India de la realidad material descrita como "Maya" o la ilusiû°n de los sentidos.
Esta maya estûÀ hecha por las infinitas interrelaciones entre tres elementos : richi, chandas y devatta que son el sujeto, el objeto y su relaciû°n, el conocimiento (espiritual: de la mente) o la percepciû°n (material: del material).
El observador de la conciencia y la realidad cuûÀntica no material crea la realidad material fenomenolû°gica.
En este sentido, la pelûÙcula Matrix es una alegorûÙa de la realidad, la û¤nica diferencia, y es importante, es que no son las mûÀquinas las que crean la realidad ilusoria sino la propia conciencia.
AsûÙ, la conciencia puede definirse como la relaciû°n del sujeto con el objeto a travûˋs de la percepciû°n o el conocimiento.
Las siguientes trûÙadas son equivalentes:
samhita_tab_es
veda filosofûÙa fûÙsica cuûÀntica
rishi tema observador conocedor observador
devatta percepciû°n (relaciû°n sujeto/objeto) observaciû°n conocimiento observable chandas objeto observado conocido resultado de la mediciû°n: valor propio del observable
Esta posiciû°n dice que entre dos mediciones no hay ningû¤n objeto y que el û¤nico objeto que existe es "el objeto observado".
El tûˋrmino clûÀsico corresponde a lo que la humanidad en su conjunto percibe de la misma manera. Pero esta posiciû°n entra en conflicto con
realidad cuûÀntica, que se percibe por tanto como totalmente paradû°jica.
y que como tal debe ser legûÙtimamente la referencia absoluta.
El problema central o pivote entre la realidad cuûÀntica y la clûÀsica es el de la decoherencia.
La decoherencia es la transiciû°n de la operaciû°n cuûÀntica a la clûÀsica.
Es decir, que cuando el sistema ha decaûÙdo, es describible clûÀsicamente porque el aspecto cuûÀntico ha desaparecido.
Al estudiar la mecûÀnica cuûÀntica, se demuestra que se reduce a las leyes de la mecûÀnica clûÀsica cuando se considera a escalas macroscû°picas.
La decoherencia es el hecho de pasar de la descripciû°n del sistema fûÙsico por una û¤nica funciû°n de onda a la de un conjunto separado de corpû¤sculos.
Cuando la funciû°n de onda de un conjunto de partûÙculas "decoheres" en el colapso de la mediciû°n el aspecto ondulatorio de la mecûÀnica cuûÀntica desaparece y sû°lo queda el aspecto de partûÙcula.
La teorûÙa fûÙsica que se ocupa de describir un gran conjunto de corpû¤sculos es la termodinûÀmica estadûÙstica, que tiene sus fundamentos en la teorûÙa cuûÀntica a travûˋs de la estadûÙstica cuûÀntica de BûÑse-Einstein y Fermi-Dirac.
Esta teorûÙa, desarrollada en el siglo XX, permite recuperar los resultados de la termodinûÀmica macroscû°pica del siglo XIX a partir de consideraciones microscû°picas.
La termodinûÀmica opera en el mundo clûÀsico de la decoherencia, mientras que la mecûÀnica cuûÀntica opera en el mundo cuûÀntico de la coherencia de onda.
La decoherencia es la transiciû°n del mundo cuûÀntico al mundo clûÀsico.
Dominar la decoherencia es el reto para producir el ordenador cuûÀntico.
Alain Aspect en su conferencia Des_objections_d_Einstein_aux_photons_jumeaux_une_nouvelle_rûˋvolution_quantique admite a este respecto (en 1H23mn) que si el ordenador cuûÀntico puede llegar a ser una realidad algû¤n dûÙa, no ve ninguna razû°n por la que el cerebro no pueda serlo.
AsûÙ, las dos realidades no fûÙsicas: la conciencia y la funciû°n de onda podrûÙan ser en realidad una y la misma.
El estado . Phi
de cualquier sistema cuûÀntico no relativista es una soluciû°n de la ecuaciû°n de SchrûÑdinger dependiente del tiempo: 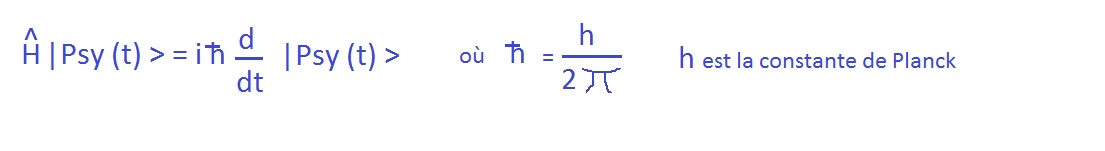 El sexto postulado es el. ûˋquation de SchrûÑdinger
.
El sexto postulado es el. ûˋquation de SchrûÑdinger
.
Esta es la ecuaciû°n dinûÀmica de la mecûÀnica cuûÀntica.
Significa simplemente que es el operador de \"energûÙa total\" del sistema, o Hamiltoniano, anotado "H", el responsable de la evoluciû°n del sistema en el tiempo.
(Tradicionalmente en la mecûÀnica cuûÀntica, los operadores reciben un sombrero para distinguirlos de otros objetos matemûÀticos como los valores propios.ecuaciû°n de SchrûÑdinger) La forma de la ecuaciû°n muestra que aplicando el operador hamiltoniano a la funciû°n de onda del sistema, obtenemos su derivada respecto al tiempo, es decir, cû°mo varûÙa en el tiempo.
(para una variaciû°n delta t del tiempo asûÙ "dt" tenemos una variaciû°n "d | Psy(t) >" de la funciû°n de onda).
AsûÙ que si aplicamos el operador hamiltoniano (ûˋnergie) a la funciû°n de onda obtenemos su evoluciû°n en el tiempo.
EstûÀ claro que es la energûÙa la que hace que las cosas sucedan.
La energûÙa y el tiempo estûÀn intrûÙnsecamente ligados.
Se dice que forman un par de variables conjugadas.
Esta ecuaciû°n sû°lo es vûÀlida en el marco no relativista.
En el marco relativista la ecuaciû°n vûÀlida es la ecuaciû°n de Klein-Gordon.
Vûˋase Olivier_castera_free_Equation_de_Schrodinger_pdf El operador hamiltoniano H estûÀ compuesto por todas las energûÙas que intervienen en el sistema.
Estas energûÙas son de dos tipos: energûÙa cinûˋtica y energûÙa potencial.
La energûÙa cinûˋtica es la energûÙa contenida en una masa en movimiento.
Un guijarro lanzado a travûˋs de una ventana la rompe en virtud de la energûÙa cinûˋtica que ha adquirido cuando se le da una determinada velocidad.
Si hay varios cristales sucesivos, cuanto mayor sea la velocidad de la piedra, mûÀs cristales atravesarûÀ.
La energûÙa potencial se debe a los campos de fuerza que se aplican al sistema.
Si se deja caer un guijarro sobre un cristal en el suelo, ganarûÀ velocidad debido a la energûÙa potencial gravitatoria que posee debido a su distancia de la tierra..
Cuanto mûÀs tiempo pasa, mûÀs se transforma la energûÙa potencial en energûÙa cinûˋtica y cuando el guijarro llega al suelo, rompe la ventana en virtud de la energûÙa cinûˋtica que ha adquirido en detrimento de su energûÙa potencial, que ha perdido.
Si lo empujas a un pozo, continuarûÀ el mismo proceso hasta que su energûÙa potencial se agote totalmente, si es que eso es posible.
Si consideramos el movimiento de un pûˋndulo (un guijarro unido a un soporte por una cuerda) este û¤ltimo oscila, es decir, desde la posiciû°n inicial (en un ûÀngulo determinado con respecto a la vertical) cuando se deja caer el guijarro, el guijarro se acelera hasta que la cuerda estûÀ vertical, luego se frena hasta que se detiene en el otro lado en una posiciû°n simûˋtrica a la posiciû°n inicial y vertical.
El pûˋndulo transforma su energûÙa potencial en energûÙa cinûˋtica y luego su energûÙa cinûˋtica en energûÙa potencial, y esto cûÙclicamente.
Si el sistema no estûÀ sometido a ninguna otra fuerza, el movimiento no se detiene.
En la prûÀctica siempre hay fuerzas de fricciû°n que disipan la energûÙa en calor hasta que se agota.
Pero este û¤ltimo punto sû°lo es cierto en la mecûÀnica clûÀsica porque en la mecûÀnica cuûÀntica no hay fricciû°n ! Otro sistema en el que existe una transformaciû°n cûÙclica entre la energûÙa potencial y la cinûˋtica es el movimiento de un satûˋlite alrededor de un planeta, por ejemplo la luna y la tierra.
La soluciû°n de la mecûÀnica clûÀsica en este caso muestra que la trayectoria del satûˋlite es una elipse, es decir, hay un momento en el que la luna estûÀ en su punto mûÀs alejado de la tierra (energûÙa potencial mûÀxima y energûÙa cinûˋtica mûÙnima, apogeo) y otro momento en el que la luna estûÀ mûÀs cerca de la tierra (energûÙa potencial mûÙnima y energûÙa cinûˋtica mûÀxima, perigeo).
Los sistemas que acabamos de describir son sistemas clûÀsicos pero tienen su correspondencia en el ûÀmbito cuûÀntico.
Por ejemplo, el modelo del pûˋndulo en la mecûÀnica cuûÀntica se llama oscilador armû°nico y el modelo del satûˋlite corresponde al modelo del ûÀtomo de hidrû°geno: un electrû°n satûˋlite de un protû°n.
En la mecûÀnica cuûÀntica, la energûÙa cinûˋtica es un operador que involucra a la masa, y la energûÙa potencial, por supuesto, tambiûˋn estûÀ representada por un operador cuya forma dependerûÀ de las energûÙas involucradas: potencial elûˋctrico y magnûˋtico, ...
La forma en que la masa estûÀ involucrada en la ecuaciû°n de Shroedinger, proviene de un trabajo anterior de Louis de Broglie que estableciû° la dualidad onda-corpû¤sculo: a cada partûÙcula de materia podemos asociar una onda cuya frecuencia es proporcional a la masa.
Esto se basa en las dos fû°rmulas de energûÙa: E = m côý que es la fû°rmula de la energûÙa de la relatividad especial de Einstein : la masa equivale a la energûÙa E = h * nu que es la relaciû°n Planck-Einstein que explica el efecto fotoelûˋctrico : la energûÙa es proporcional a la frecuencia.
AsûÙ vemos que en la ecuaciû°n de Shroedinger se integra un resultado de la relatividad especial de Einstein.
Es importante entender que las energûÙas implicadas ejercen una restricciû°n sobre el sistema, es decir, sobre la funciû°n de onda.
Cuando se trata de sistemas oscilantes como el oscilador armû°nico (pûˋndulo) o el ûÀtomo de hidrû°geno (satûˋlites)El efecto de la restricciû°n energûˋtica es localizar la funciû°n de onda en una regiû°n del espacio.
Por ejemplo, un sistema clûÀsico sometido a ninguna fuerza (un meteorito que se pierde en el espacio interestelar, donde las fuerzas gravitatorias de las estrellas pueden despreciarse) se moverûÀ en lûÙnea recta indefinidamente.
El equivalente cuûÀntico es una onda plana que se propaga indefinidamente, como un fotû°n que no estûÀ sometido a ninguna fuerza (los fotones son partûÙculas sin masa ni carga elûˋctrica de ningû¤n tipo y, por tanto, no estûÀn sometidos a ninguna fuerza o energûÙa).
Cuando la funciû°n de onda tiene una soluciû°n cûÙclica (funciû°n de onda localizada) el tiempo ya no tiene el efecto de alejar indefinidamente las partes del sistema.
El electrû°n permanecerûÀ situado cerca de su nû¤cleo, que es el protû°n en el caso del ûÀtomo de hidrû°geno.
Al mismo tiempo, si la onda cuûÀntica se propaga cûÙclicamente en una regiû°n finita, se superpone a sûÙ misma y, por lo tanto, interfiere consigo misma de forma constructiva o destructiva.
Al resolver la ecuaciû°n de Shroedinger de tales sistemas, se observa que el tiempo ya no interviene en la forma de la funciû°n de onda y que sû°lo es el espacio (la posiciû°n) que determina la forma de la onda.
Este es el caso de ondes_stationnaires_es que ya se ha mencionado.
Es decir, los lugares donde la interferencia es constructiva son siempre los mismos que los lugares donde es destructiva.
La onda estacionaria es un concepto poderoso que nos permite entender cû°mo un fenû°meno estûÀtico puede surgir de un fenû°meno dinûÀmico.
Este es uno de los elementos que permite la integraciû°n de la visiû°n cuûÀntica: toda la estabilidad de la materia que experimentamos proviene de una maraûÝa de ondas en constante movimiento pero cuya resultante de interferencia es estable.
Para el ûÀtomo, esto da orbitales bien definidos cuyas formas son proporcionadas por las funciones de soluciû°n de la ecuaciû°n de Shroedinger, los orbitales atû°micos: las nubes son las nubes de probabilidades de presencia del electrû°n.
Cuanto mûÀs densa es la nube, mayor es la probabilidad de que el electrû°n estûˋ presente.
 Representaciû°n de la amplitud de probabilidad de las ondas estacionarias (armû°nicos) del oscilador armû°nico.
Representaciû°n de la amplitud de probabilidad de las ondas estacionarias (armû°nicos) del oscilador armû°nico.
Obsûˋrvese el parecido con los estados de vibraciû°n (Nodos de vibraciû°n y vientres) de una cuerda que vibra.
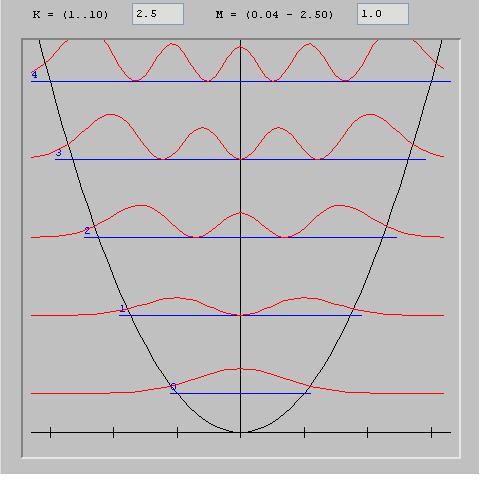
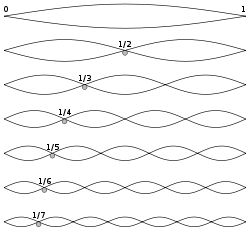 Observamos que en el caso cuûÀntico (a la izquierda) la amplitud de probabilidad de las funciones de onda (en rojo) disminuye progresivamente a medida que se aleja del centro, es decir, en las regiones donde el potencial se hace mûÀs fuerte (curva parabû°lica en negro) pero nunca es completamente cero.
Observamos que en el caso cuûÀntico (a la izquierda) la amplitud de probabilidad de las funciones de onda (en rojo) disminuye progresivamente a medida que se aleja del centro, es decir, en las regiones donde el potencial se hace mûÀs fuerte (curva parabû°lica en negro) pero nunca es completamente cero.
Por tanto, existe la posibilidad de que la partûÙcula se encuentre en una regiû°n remota donde la energûÙa potencial es mayor que la energûÙa cinûˋtica, mientras que clûÀsicamente quedarûÙa atrapada en la regiû°n donde el potencial es menor que su energûÙa cinûˋtica..
Este hecho es la razû°n de laeffet_tunnel que permite a una partûÙcula cuûÀntica atravesar una barrera de potencial cuya energûÙa es superior a la de la partûÙcula porque la funciû°n de onda no es nula al otro lado de la barrera permitiendo que la partûÙcula sea observada allûÙ.
Esto es una consecuencia del aspecto no local de la funciû°n de onda.
Se trata de la restricciû°n que la energûÙa impone a la funciû°n de onda para permanecer localizada y asûÙ interferir consigo misma para producir ondas estacionarias asociadas a valores particulares de energûÙa (Por lo tanto, los valores cuantificados) que es el origen del concepto de "cuantificaciû°n".
Por û¤ltimo, es necesario hablar de lo que estûÀ en el origen de la teorûÙa cuûÀntica: la constante_de_Planck que aparece en la ecuaciû°n de Shroedinger.
Esta constante fue introducida por el fûÙsico Max_Planck explicar el valor de la radiaciû°n tûˋrmica de la materia en funciû°n de la temperatura.
La ley observada que sigue esta radiaciû°n nos obliga a considerar que la energûÙa tûˋrmica no se emite de forma continua sino en paquetes o "cuantos"..
Esta es la primera evidencia de la naturaleza cuûÀntica de la materia.
En fûÙsica, la acciû°n se define como el producto de la energûÙa y el tiempo.
Es bastante intuitivo: cuando una energûÙa actû¤a durante un tiempo determinado genera una determinada acciû°n cuyo valor es proporcional al de la energûÙa y a la duraciû°n del tiempo en que actû¤a.
La constante de Planck representa la acciû°n mûÀs pequeûÝa posible en el mundo fûÙsico.
Es una constante universal de la fûÙsica que caracteriza la naturaleza cuûÀntica de la realidad.
El valor de esta constante es extremadamente pequeûÝo: 6,62607004 û 10-34 m2 kg / s pero, sin embargo, es distinto de cero.
que se denominan unidades Planck.
AsûÙ, el mundo fûÙsico tal como lo describe la mecûÀnica cuûÀntica tiene un lûÙmite en lo infinitamente pequeûÝo mûÀs allûÀ del cual ya no podemos hablar en tûˋrminos de fûÙsica, es finalmente un lûÙmite del mundo fûÙsico.
Si hay un borde, un lûÙmite, es una restricciû°n cuûÀntica natural para la funciû°n de onda y, por tanto, para la cuantizaciû°n (que es en sûÙ mismo, como hemos visto, una fuerza).
La constante de Planck define la pixelaciû°n del Universo.
El origen mûÀs fundamental de la cuantificaciû°n se encuentra tambiûˋn en el funcionamiento de la conciencia, que por naturaleza no es continua.
En efecto, si consideramos la observaciû°n por un sujeto de un objeto que es un punto de vista en la conciencia, ûˋsta sû°lo es posible por la discriminaciû°n de la conciencia de los diferentes puntos de vista posibles.
Para que se identifiquen, los puntos de vista deben ser distintos, de lo contrario todos los puntos de vista se fusionarûÙan y no habrûÙa una verdadera observaciû°n.
La discriminaciû°n es la cualidad del intelecto que, en este sentido, es una propiedad fundamental de la conciencia.
Encontramos asûÙ los elementos presentes en los postulados cuûÀnticos de la mediciû°n.
"
1.5.1.AnûÀlisis del aforismo
poema coincidencia cuûÀntica enlace a los postulados
ô¢Quûˋ es? la funciû°n de onda o vector de estado o "ket" (de corchete , gancho en francûˋs) . Premier postulat
posible la estructura probabilûÙstica de la funciû°n de onda, los diferentes estados propios posibles del ket . Troisiû´me postulat se logra la dinûÀmica del operador hamiltoniano energûÙa total del sistema responsable de la evoluciû°n. . Deuxiû´me postulat bajo el ojo de la conciencia los postulados de la mediciû°n, es decir, la necesaria intervenciû°n del observador . Quatriû´me postulat sû°lo se logra lo que es posible sû°lo se pueden obtener los valores propios del observable y el estado del sistema es entonces el correspondiente estado propio. . Cinquiû´me postulat Lo que es posible se logra la ecuaciû°n de SchrûÑdinger, la ecuaciû°n de la dinûÀmica cuûÀntica. . Sixiû´me postulat
La gran dificultad que tienen los cientûÙficos para aceptar el mensaje de la teorûÙa cuûÀntica explica por quûˋ tan pocas personas pueden acceder a ella.
AquûÙ encontrarûÀ un resumen de esta situaciû°n, analizada por Jean Staune e informada por Bruno Lussato: bruno_lussato_les_plus_grandes_dûˋsinformations_de_l_histoire_des_sciences
(blog donde, en 2009, dejûˋ un relato de la conferencia que Alain Aspect dio en 1982 en Toulouse cuando recorrûÙa las universidades de Francia para presentar los resultados de sus trabajos.bruno lussato la mayor desinformaciû°n de la historia de la ciencia nweb) Este texto podrûÙa haber sido escrito, y probablemente mucho mejor, por un gran nû¤mero de personas conocedoras que forman parte del "establishment" cientûÙfico, pero su reticencia a hacerlo me ha llevado, por un lado, a poder reservar el nombre de dominio quantum.
org que curiosamente estaba disponible y por otro lado dedicar decenas de horas a elaborar este texto que probablemente estûˋ aû¤n por mejorar...
Los postulados obviamente no incluyen al observador en el sistema fûÙsico
sino que declara su existencia necesaria para que se produzca una observaciû°n o
se produce un resultado fûÙsico.
Esto encaja perfectamente con las concepciones de los chamanes sobre el "sueûÝo del mundo"..
La diferencia con la realidad es que la simulaciû°n hologrûÀfica del mundo no se fabrica
por ordenadores materiales, sino por un ordenador cû°smico no material que se identifica
a la conciencia en su concepciû°n mûÀs amplia.