1.Moebius et structure de l'espace quantique
1.1.Anneau de moebius fluctuation du vide
l'anneau de moebius semble un bon modèle pour les fluctuations du vide quantique.
en effet si l'on scinde en deux un anneau de moebius par le milieu de la bande alors sa topologie
change et l'on obtient un seul ruban simple enroulé d'un tour complet sur lui-même
alors que l'anneau de moebius est enroulé d'un demi-tour sur lui-même.
si on réitère cette opération sur les anneaux scindés alors la topologie ne change plus et l'on duplique par scission
des rubans de même topologie.
si on scinde l'anneau non pas au milieu mais sur un bord (1/3 de la largeur par exemple) alors on obtiendra un résultat différent :
- du petit côté 1/3 au aura un anneau qui fait un tour complet sur lui même
- du grand côté 2/3 on restera avec anneau de moebius c'est à dire avec un demi-tour simplement.
ceci peut-être rapproché avec le demi-quantum des particules virtuelles (fluctuation de l'état fondamental du champ dit état de vide car il n'y a pas de particules réelles dans cet état fondamental )
et le quantum entier des particules réelles: état du champ à une, deux, n particules réelles (avec une scission d'un tier/deux-tiers on garde l'anneau de moebius qui génére une
infinité d'anneau à 1 tour).
la topologie de moebius correspondrait donc au virtuel ou non-manifesté.
il y a en fait deux anneaux de moebius possibles selon que l'on tourne le ruban de papier
à droite où à gauche avant de le coller, le résultat ne sera pas le même.
Les rubans de moebius ont donc deux hélicités possible ce qui peut représenter le spin droit ou gauche.
Le physicien Jean-Pierre Petit utilise cette géométrie à travers le monoèdre
qui est un anneau de Moebius "épaissi".
le_monoedre_un_polyèdre_qui_n_a_qu_une_face_qu_une_seule_arête_et_pas_de_sommet_2023_09_27 ;https://www.youtube.com/watch?v=NCaoYQCAFT4;
1.2.Ruban de moebius tetraedre
Si l'on étire un ruban de moebius suivant des segments opposés les contraintes
de résistance du ruban conduise à positionner les segments à 90° l'un de l'autre.
Les extrémités des segments correspondent aux sommets d'un tétraèdre.
l'angle de 90° (la croix) et le tétraèdre apparaissent alors naturellement
à partir de la topologie du ruban de Moebius.
Le tétraèdre étant la base du modèle du vide quantique de la Théorie de Nassim Haramein
c'est un élément de plus pour considérer l'anneau de Moebius.
1.3.Coeur de moebius
si on imbrique deux rubans de moebius d'hélicité différentes alors on obtient la forme d'un coeur en 3D
Dynamique du vide quantique et battement d'un coeur par Nassim Haramein :
dynamique_du_vide_quantique_et_battement_d_un_coeur_par_Nassim_Haramein_2015_06_20
1.4.Ruban de moebius triangle equilateral
si on construit un ruban de moebius avec un feuille de papier en le tendant au maximum,
c'est à dire en essayant de serrer au maximum la boucle alors le résultat final en
applatissant la structure est un triangle équilatéral avec plusieurs feuillets.
il y a un feuillet central qui peut être basculé d'un côté ou de l'autre ce qui
fait penser au battement d'un coeur (oreillette ventricule).
le coeur humain est composé de deux coeurs: un pour la circulation artérielle,
et un pour la circulation veineuse, comme dans l'image ci-dessus avec les deux anneaux de möbius imbriqués d'hélicités différentes.
l'imbrication de deux tétraèdres forme l'étoile tétraédrique.
la démonstration mathématique de ce triangle a été faite par le mathématicien Richard Evan Schwartz :
the_optimal_paper_moebius_band_richard_evan_schwartz_september_12_2023_2023_09_15 ;https://arxiv.org/pdf/2308.12641.pdf;
1.5.Angle de moebius
C'est en regardant la conférence vraiment passionnante et inspirante de Tadashi Tokieda : science_à _partir_d_une_feuille_de_papier
que j'ai eu l'idée de d'aplatir un anneau de Moebius.
Bien que le triangle de Moebius soit de fait un anneau de Moebius aplati et que l'angle dans ce cas est forcément 60° *3 =180°
qu'en est il d'un anneau de Moebius quelconque que l'on aplati ?
on obtient alors en projection plane un polygone qui sera différent suivant
les dimensions du ruban de papier mais qui présentera toujours un angle entre deux côtés opposés qui semble être toujours le même.
on peut réaliser plusieurs polygones de cette manière et tracer sur une feuille cet angle
test de mesure de cet angle avec deux rubans de tailles différentes :
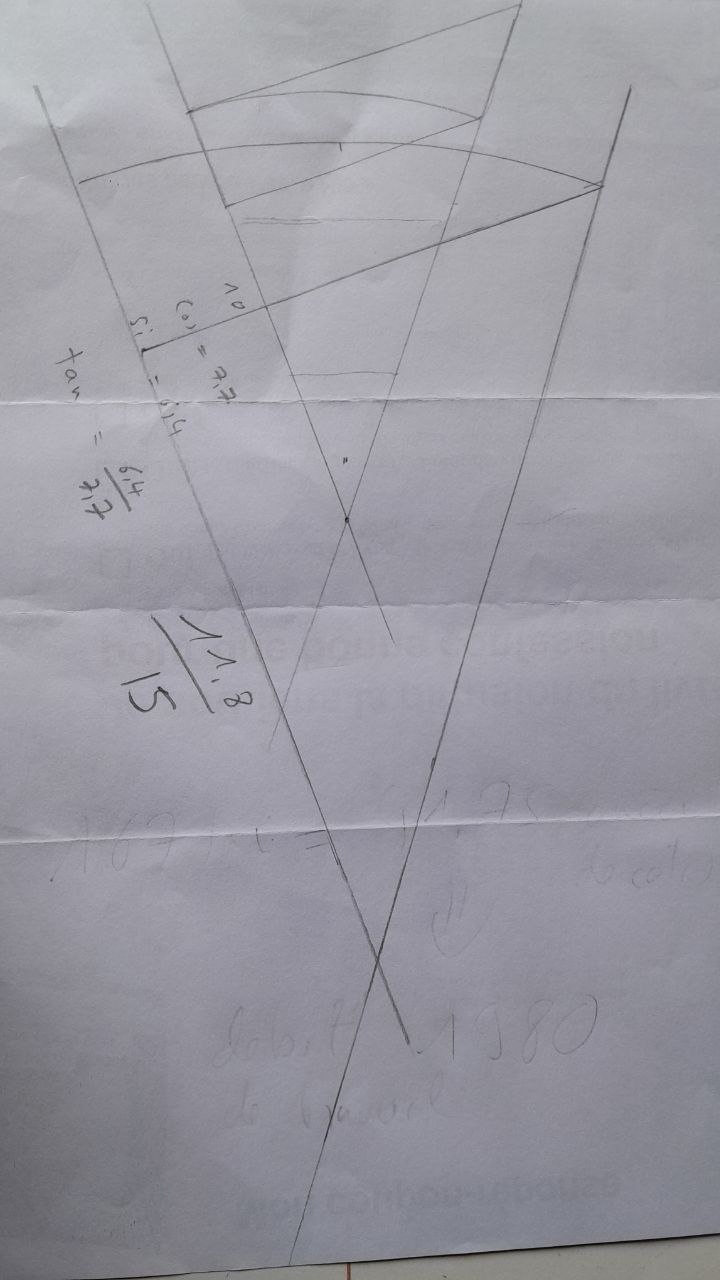
setprec=2
set sinM1 = 6.4;
set cosM1 = 7.7;
set sinM2 = 11.8;
set cosM2 = 15;
set tanM = sinM/cosM;
tanM=0
set angle_en_degre(s,c) = arctan(s/c) * 180 / pi;
angle_en_degre(sinM1,cosM1) =39.73
angle_en_degre(sinM2,cosM2) =38.19
" moyenne :
angle_en_degre(sinM1,cosM1)
+angle_en_degre(sinM2,cosM2)
=77.92 / 2 =38.96
# si on divise par deux cet angle on obtient :
/ 2 =19.48
(calcul réalisé avec le calculateur algébrique scalc )
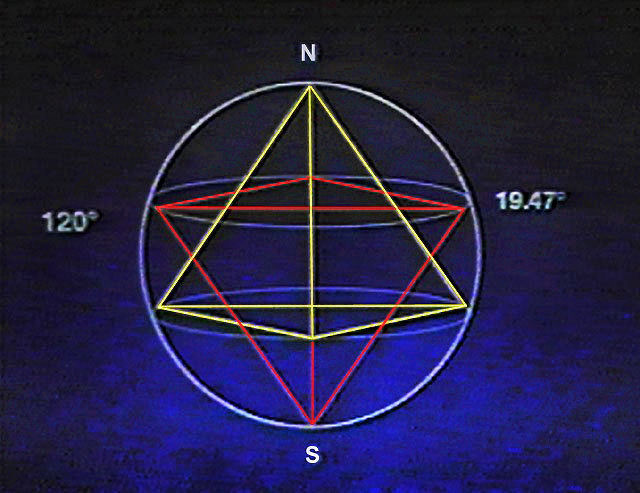
qui se rapproche de l'angle de 19.47 entre l'équateur d'une sphère et des 3 points de contacts des sommets d'un tétraèdre qui s'inscrit dans cette sphère.
Le pôle étant le 4ième sommet du tétraèdre (cf étoile tétraédrique).
Il faudrait une étude mathématique pour déterminer l'existence et la valeur de cet angle.
On peut faire des expériences avec de nombreux anneaux de Moebius de taille prédéfinie
avec différents rapports longueur sur largeur.
L'existence de cet angle pose un problème particulier :
L'angle est une notion géométrique, l'anneau de Moebius est un objet topologique.
Un ruban de papier est rigide et ne peut-être déformé mais il peut-être plié.
On passe donc ainsi d'un objet topologique à un objet géométrique.
L'écrasement du ruban semble être une opération difficile à décrire mathématiquement car à partir d'un même anneau on peut obtenir
plusieurs résultats selon la façon dont on l'a écrasé.
Pourtant il semble bien que l'on trouvera toujours le même angle entre deux faces opposés du polygone résultant.
Dans le cas de l'étoile tétraédrique, le calcul de l'angle est un problème géométrique.
Dans le cas de l'anneau, il ne semble pas évident que cela soit un problème géométrique.
Par la géométrie on peut générer un nombre transcendant comme pi : rapport entre la circonférence et le diamètre d'un cercle.
On peut se poser la question de la nature mathématique de l'angle de Moebius: est-ce un simple nombre géométrique ou un nombre transcendant ?