1.Moebius
Moebius e la struttura dello spazio quantistico
1.1.Fluttuazione del vuoto dell'anello di moebius
l'anello di moebius sembra un buon modello per le fluttuazioni del vuoto quantistico.
Infatti, se dividiamo un anello di Moebius in due per il centro della banda, la sua topologia
e otteniamo un nastro singolo avvolto su se stesso per un giro completo.
mentre l'anello di Moebius è avvolto per mezzo giro su se stesso.
Se si ripete questa operazione sugli anelli divisi, la topologia non cambia piĂą e si duplica dividendo
nastri con la stessa topologia.
se l'anello è spaccato non al centro ma su un bordo (1/3 della larghezza, ad esempio) si ottiene un risultato diverso :
- sul lato corto 1/3 dell'anello compie un giro completo su se stesso
- sul lato lungo 2/3, rimarremo con l'anello di moebius, cioè con un semplice mezzo giro.
questo può essere paragonato al mezzo quantum di particelle virtuali (fluttuazione dello stato fondamentale del campo, chiamato stato di vuoto perché non ci sono particelle reali. )
e l'intero quantum di particelle reali: stato del campo con una, due o n particelle reali (con una suddivisione di un terzo/due terzi, manteniamo l'anello di moebius che genera un
anelli infiniti a 1 giro).
La topologia di Moebius corrisponderebbe quindi alla topologia virtuale o immanifestata..
Ci sono in effetti due possibili anelli di Moebius, a seconda di come si gira il nastro di carta
a destra o a sinistra prima di incollarlo, il risultato non sarĂ lo stesso..
I nastri di Moebius sono quindi due possibili elicitĂ che possono rappresentare lo spin destro o sinistro..

Se si intrecciano due nastri di Moebius di diversa elicitĂ , si ottiene la forma di un cuore 3D.

1.2.Ruban de moebius tetraedre
Se allunghiamo una striscia di moebius lungo segmenti opposti, le sollecitazioni
La resistenza del nastro porta i segmenti a posizionarsi a 90° l'uno rispetto all'altro..
Gli estremi dei segmenti corrispondono ai vertici di un tetraedro.
l'angolo di 90° (la croce) e il tetraedro appaiono naturalmente
dalla topologia del nastro di Moebius.


Il tetraedro è alla base del modello di vuoto quantistico del . Théorie de Nassim Haramein
è un elemento in più per considerare l'anello di Moebius.
1.3.Angolo di moebius
se appiattiamo una striscia di Moebius, otteniamo un poligono in proiezione planare che si differenzia in base a
la piega, ma avrĂ sempre un angolo tra due lati opposti che sembra essere lo stesso.

è possibile creare diversi poligoni in questo modo e tracciare questo angolo su un foglio di carta
test per misurare questo angolo con due nastri di dimensioni diverse :
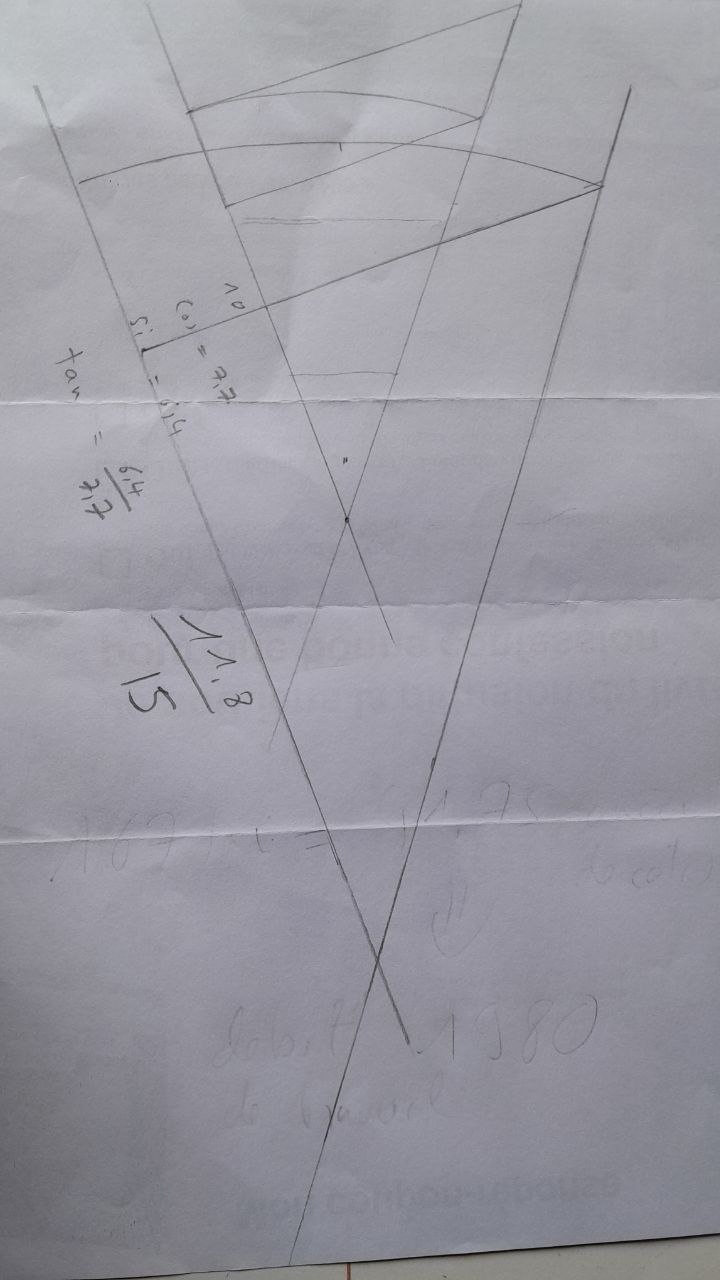
setprec=3
impostare sinM = 6.4;
impostare cosM = 7.7;
impostare sinM = 11.8;
impostare cosM = 15;
impostare tanM = sinM/cosM;
tanM=0.787
#arctan(tanM) * 180 / pi =39.73 °
arctan(tanM) * 180 / pi =38.191 °
media :
19.86
19.09
=38.95
dividere questo angolo per due per ottenere :
38.95 / 2 =19.475
(calcolo con la calcolatrice algebrica scalc )
che è prossimo all'angolo tra l'equatore di una sfera e i 3 punti di contatto dei vertici di un tetraedro inscritto in questa sfera.
Il polo è il 4° vertice del tetraedro (cf ).
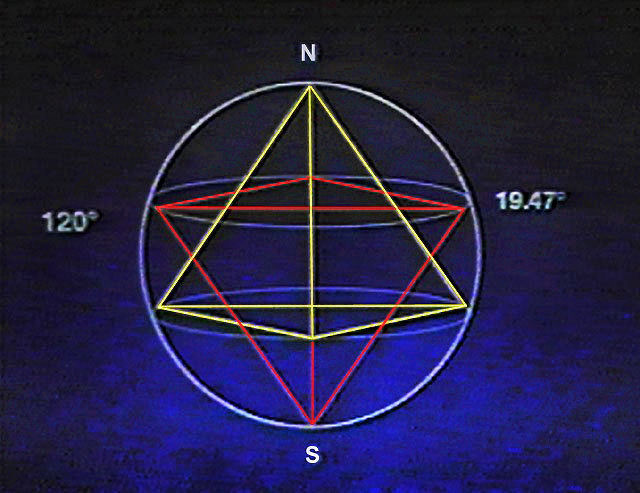
Sarebbe necessario uno studio matematico per determinare l'esistenza e il valore di questo angolo..
2.Ruban de moebius triangolo equilatero
Se si costruisce una striscia di Moebius da un foglio di carta allungandola il più possibile, cioè cercando di stringere il più possibile l'anello, il risultato finale, appiattendo la struttura, è un triangolo equilatero con più fogli..
c'è un foglietto centrale che può essere inclinato da un lato o dall'altro, ricordando il battito del cuore (atrio ventricolo).
il cuore umano è composto da due cuori: uno per la circolazione arteriosa e uno per la circolazione venosa, come nell'immagine sopra con i due anelli di Mobius annidati di diversa elicità .
l'incastro di due tetraedri forma la stella_tetraedrica.







