1.Moebius
Moebius y la estructura del espacio cuántico
1.1.Fluctuación del vacÃo del anillo de moebius
el anillo de moebius parece un buen modelo para las fluctuaciones del vacÃo cuántico.
De hecho, si partimos un anillo de Moebius en dos por la mitad de la banda, entonces su topologÃa
cambia y obtenemos una única cinta enrollada una vuelta completa sobre sà misma
mientras que el anillo de Moebius se enrolla media vuelta sobre sà mismo.
si repetimos esta operación en los anillos divididos entonces la topologÃa ya no cambia y duplicamos dividiendo
cintas con la misma topologÃa.
si el anillo no está partido por la mitad, sino por uno de los bordes (1/3 de la anchura, por ejemplo) entonces obtenemos un resultado diferente :
- en el lado corto 1/3 del anillo da una vuelta completa sobre sà mismo
- en el lado largo 2/3, nos quedaremos con el anillo de moebius, es decir, con una simple media vuelta.
esto se puede comparar con el medio quantum de partÃculas virtuales (fluctuación del estado fundamental del campo, llamado estado de vacÃo porque no hay partÃculas reales )
y todo el cuanto de partÃculas reales: estado del campo con una, dos o n partÃculas reales (con una división de un tercio/dos tercios, mantenemos el anillo de moebius que genera un
anillos infinitos de 1 vuelta).
la topologÃa moebius corresponderÃa, por tanto, a lo virtual o no manifestado.
de hecho, hay dos posibles anillos de Moebius, dependiendo de cómo gire la cinta de papel
a la derecha o a la izquierda antes de pegarlo, el resultado no será el mismo.
Las cintas de Moebius son, por tanto, dos helicidades posibles, que pueden representar el espÃn derecho o el izquierdo..
si entrelazas dos cintas de Moebius de diferente helicidad, obtienes la forma de un corazón en 3D.
1.2.Ruban de moebius tetraedre
Si estiramos una banda de Moebius a lo largo de segmentos opuestos, las tensiones
la resistencia de la cinta hace que los segmentos se coloquen a 90° entre sÃ.
Los extremos de los segmentos corresponden a los vértices de un tetraedro.
el ángulo de 90 (la cruz) y el tetraedro aparecen de forma natural
de la topologÃa de la banda de Moebius.
El tetraedro es la base del modelo de vacÃo cuántico del . Théorie de Nassim Haramein
es un elemento más para considerar el anillo de Moebius.
1.3.ángulo de moebius
si aplanamos una banda de Moebius, obtenemos un polÃgono en proyección plana que es diferente según
el pliegue, pero siempre tendrá un ángulo entre dos lados opuestos que parece ser el mismo.
puede crear varios polÃgonos de esta manera y trazar este ángulo en una hoja de papel
prueba para medir este ángulo con dos cintas de diferentes tamaños :
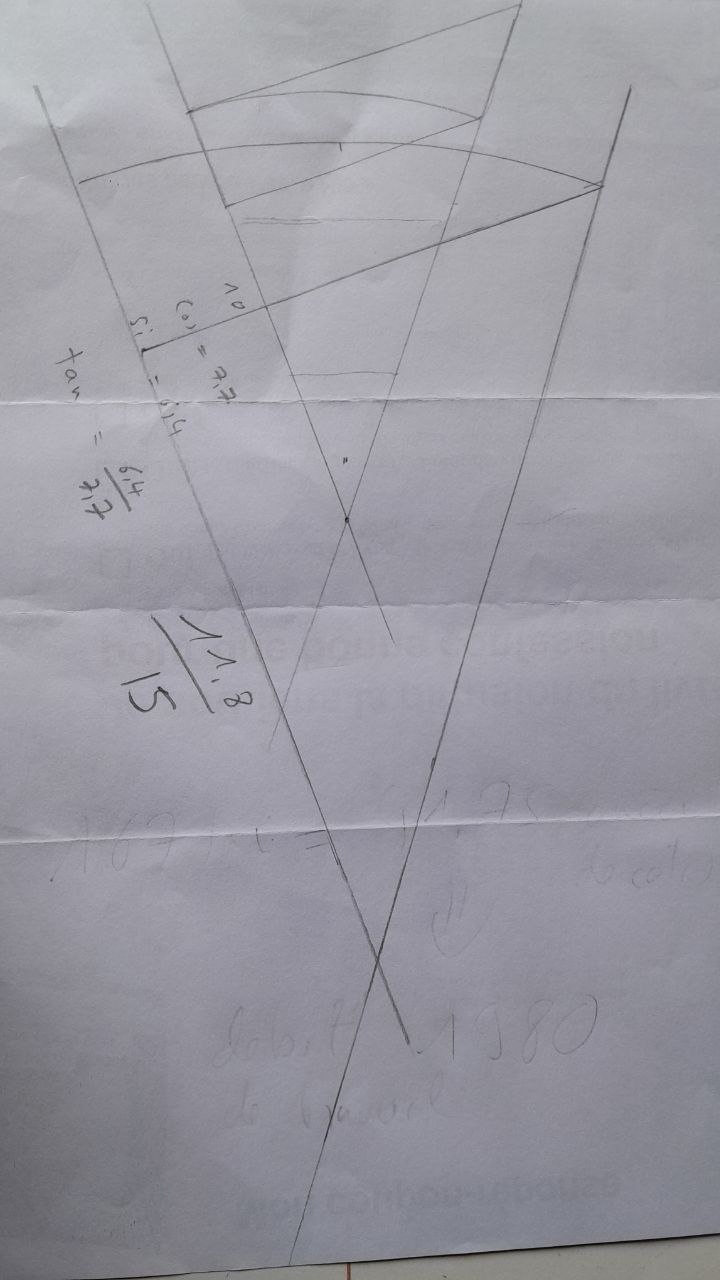
setprec=3
set sinM = 6.4;
set cosM = 7.7;
set sinM = 11.8;
set cosM = 15;
set tanM = sinM/cosM;
tanM=0.787
#arctan(tanM) * 180 / pi =39.73 °
arctan(tanM) * 180 / pi =38.191 °
media :
19.86
19.09
=38.95
divida este ángulo por dos para obtener :
38.95 / 2 =19.475
(cálculo con calculadora algebraica scalc )
que es próximo al ángulo entre el ecuador de una esfera y los 3 puntos de contacto de los vértices de un tetraedro inscrito en esta esfera.
Siendo el polo el 4º vértice del tetraedro (cf ).
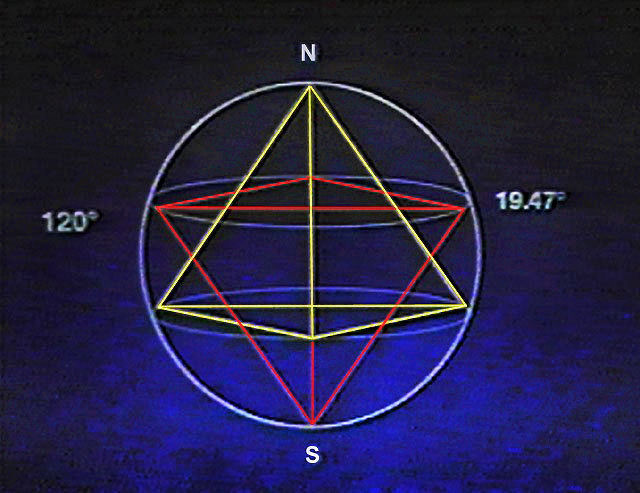
SerÃa necesario un estudio matemático para determinar la existencia y el valor de este ángulo..
2.Ruban de moebius triángulo equilátero
Si se construye una banda de Moebius a partir de una hoja de papel estirándola al máximo, es decir, intentando apretar el bucle lo máximo posible, el resultado final, al aplanar la estructura, es un triángulo equilátero con varias hojas..
hay una valva central que puede inclinarse hacia un lado u otro, recordando el latido de un corazón (aurÃcula ventrÃculo).
el corazón humano está formado por dos corazones: uno para la circulación arterial y otro para la circulación venosa, como en la imagen superior con los dos anillos de Mobius anidados de diferente helicidad.
el entrelazamiento de dos tetraedros forma la estrella_tetraédrica.