1.Moebius
Moebius en de structuur van kwantumruimte
1.1.Moebius ring vacuÞm fluctuatie
de moebiusring lijkt een goed model voor kwantum vacuÞmfluctuaties.
In feite, als we een Moebiusring in tweeÃŦn delen door het midden van de band, dan is de topologie
verandert en we krijgen een enkel lint dat ÃĐÃĐn volledige omwenteling op zichzelf is gewikkeld
terwijl de Moebiusring een halve slag op zichzelf is gewikkeld.
als we deze operatie herhalen op de gesplitste ringen dan verandert de topologie niet meer en dupliceren we door te splitsen
linten met dezelfde topologie.
als de ring niet in het midden maar aan ÃĐÃĐn rand is gespleten (1/3 van de breedte, bijvoorbeeld) dan krijgen we een ander resultaat :
- aan de korte kant maakt 1/3 van de ring een volledige draai om zichzelf
- aan de 2/3 lange zijde blijven we bij de moebiusring, dus met een eenvoudige halve draai.
dit kan worden vergeleken met het halve kwantum van virtuele deeltjes (fluctuatie van de fundamentele toestand van het veld, bekend als de vacuÞmtoestand omdat er geen echte deeltjes zijn )
en het hele kwantum van echte deeltjes: toestand van het veld met ÃĐÃĐn, twee of n echte deeltjes (met een derde/twee derde verdeling, houden we de moebiusring die een
oneindige 1-draai ringen).
de moebiustopologie zou daarom overeenkomen met de virtuele of niet-gemanifesteerde.
er zijn in feite twee mogelijke Moebiusringen, afhankelijk van hoe je het papierlint draait
naar rechts of naar links voordat je het plakt, zal het resultaat niet hetzelfde zijn..
De moebiuslinten zijn daarom twee mogelijke heliciteiten die de rechter- of linkerspin kunnen voorstellen..

Als je twee Moebiuslinten van verschillende helix door elkaar weeft, krijg je de vorm van een 3D-hart.

1.2.Ruban de moebius tetraedre
Als we een Moebiusstrook uitrekken langs tegenovergestelde segmenten, dan zijn de spanningen
weerstand van het lint leidt ertoe dat de segmenten onder een hoek van 90° ten opzichte van elkaar staan.
De uiteinden van de segmenten komen overeen met de hoekpunten van een tetraÃŦder.
de hoek van 90 (het kruis) en de tetraÃŦder verschijnen op natuurlijke wijze
van de topologie van de Moebiusstrook.


De tetraÃŦder is de basis van het kwantumvacuÞmmodel van de . ThÃĐorie de Nassim Haramein
het is nog een element om de Moebiusring te overwegen.
1.3.Angle de moebius
als we een Moebiusstrook afvlakken, krijgen we een veelhoek in vlakke projectie die verschillend is volgens
de vouw, maar zal altijd een hoek hebben tussen twee tegenover elkaar liggende zijden die hetzelfde lijkt te zijn.

je kunt op deze manier meerdere veelhoeken maken en deze hoek uitzetten op een vel papier
test om deze hoek te meten met twee banden van verschillende grootte :
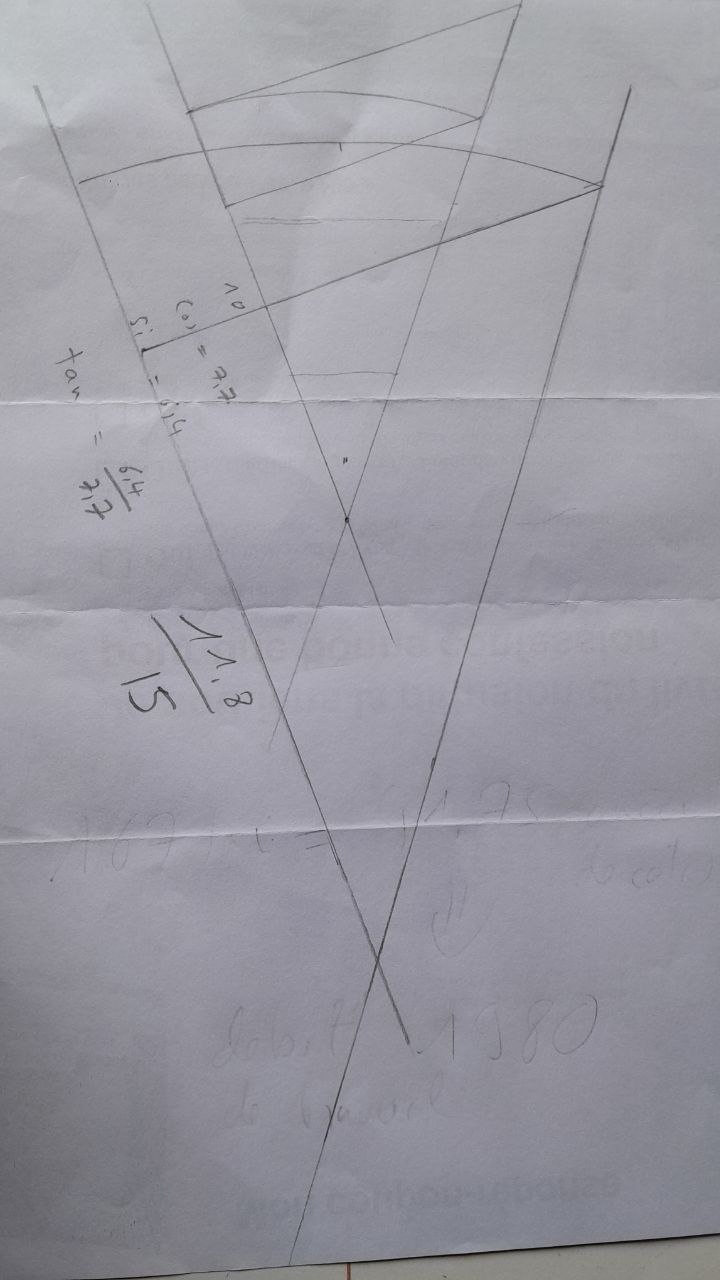
setprec=3
set sinM = 6.4;
instellen cosM = 7.7;
set sinM = 11.8;
instellen cosM = 15;
stel tanM = sinM/cosM;
tanM=0.787
#arctan(tanM) * 180 / pi =39.73 °
arctan(tanM) * 180 / pi =38.191 °
gemiddelde :
19.86
19.09
=38.95
Deel deze hoek door twee om het volgende te krijgen :
38.95 / 2 =19.475
(berekening met de algebraÃŊsche rekenmachine scalc )
die dicht bij de hoek ligt tussen de evenaar van een bol en de 3 raakpunten van de hoekpunten van een tetraÃŦder ingeschreven in deze bol.
De pool is het 4e hoekpunt van de tetraÃŦder (cf ).
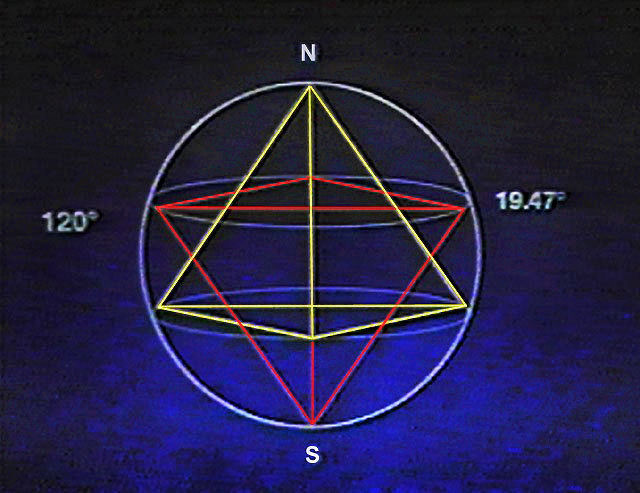
Er is een wiskundig onderzoek nodig om het bestaan en de waarde van deze hoek te bepalen..
2.Ruban de moebius driehoek gelijkzijdig
Als je een Moebiusstrook construeert uit een vel papier door het zo strak mogelijk uit te rekken, d.w.z. door te proberen de lus zo strak mogelijk te maken, dan is het eindresultaat, door de structuur plat te maken, een gelijkzijdige driehoek met meerdere vellen..
er is een centraal blaadje dat naar de ene of de andere kant kan worden gekanteld, wat doet denken aan een hartslag (boezem hartkamer).
het menselijk hart bestaat uit twee harten: ÃĐÃĐn voor de arteriÃŦle circulatie en ÃĐÃĐn voor de veneuze circulatie, zoals in de afbeelding hierboven met de twee geneste Mobius ringen met verschillende heliciteit.
het in elkaar grijpen van twee tetraÃŦders vormt de tetrahedral_star.







