1.Moebius
Moebius und die Struktur des Quantenraums
1.1.Moebiusring Vakuumfluktuation
der moebius-ring scheint ein gutes modell fû¥r fluktuationen im quantenvakuum zu sein.
Denn wenn man einen Moebiusring durch die Mitte des Bandes in zwei Teile spaltet, dann ist seine Topologie
ûÊndert sich und man erhûÊlt ein einziges einfaches Band, das eine volle Umdrehung um sich selbst gewickelt ist
wûÊhrend der Moebiusring um eine halbe Umdrehung um sich selbst gedreht ist.
wenn wir diese Operation an den gespaltenen Ringen wiederholen, dann ûÊndert sich die Topologie nicht mehr und wir duplizieren durch Spaltung
BûÊnder mit derselben Topologie.
wenn man den Ring nicht in der Mitte, sondern an einem Rand spaltet (1/3 der Breite z. B.) dann erhalten wir ein anderes Ergebnis :
- auf der kurzen Seite 1/3 au wird einen Ring haben, der sich einmal um sich selbst dreht
- Auf der langen Seite 2/3 bleibt man beim Moebiusring, d. h. man dreht sich einfach um..
dies kann mit dem Halbquantum der virtuellen Teilchen verglichen werden (Fluktuation des Grundzustands des Feldes, der als Vakuumzustand bezeichnet wird, da es keine realen Teilchen gibt. )
und das gesamte Quantum der realen Teilchen: Zustand des Feldes mit einem, zwei, n realen Teilchen (Bei einer Aufspaltung um ein Drittel/Zwei Drittel bleibt der Moebiusring erhalten, der eine
unendlich viele 1-Runden-Ringe).
die Moebius-Topologie wû¥rde also dem Virtuellen oder Unmanifestierten entsprechen.
es gibt tatsûÊchlich zwei mûÑgliche Moebius-Ringe, je nachdem, wie man den Papierstreifen dreht
rechts oder links, bevor Sie es aufkleben, wird das Ergebnis nicht das gleiche sein.
Die MoebiusbûÊnder sind also zwei mûÑgliche HelizitûÊten, was den rechten oder linken Spin darstellen kann.

wenn man zwei MoebiusbûÊnder mit unterschiedlicher HelizitûÊt ineinander schachtelt, erhûÊlt man die Form eines Herzens in 3D

1.2.Ruban de Moebius Tetraedre
Wenn man ein Moebiusband entlang gegenû¥berliegender Segmente dehnt, sind die Spannungen
des Bandwiderstandes dazu fû¥hrt, dass die Segmente in einem Winkel von 90ô¯ zueinander positioniert werden.
Die Enden der Segmente entsprechen den Eckpunkten eines Tetraeders..
der 90ô¯-Winkel (das Kreuz) und das Tetraeder erscheinen dann natû¥rlich
aus der Topologie des Moebiusbands.


Da der Tetraeder die Grundlage fû¥r das Modell des Quantenvakuums der Thûˋorie de Nassim Haramein de
es ist ein weiteres Element, um den Moebiusring zu betrachten.
1.3.MûÑbiuswinkel
Wenn wir ein Moebiusband flachlegen, erhalten wir in der Ebenenprojektion ein Polygon, das sich wie folgt unterscheidet
die Faltung, die aber immer einen Winkel zwischen zwei gegenû¥berliegenden Seiten aufweisen wird, der immer gleich zu sein scheint.

man kann mehrere Polygone auf diese Weise herstellen und diesen Winkel auf einem Blatt einzeichnen
Test zur Messung dieses Winkels mit zwei unterschiedlich groûen BûÊndern :
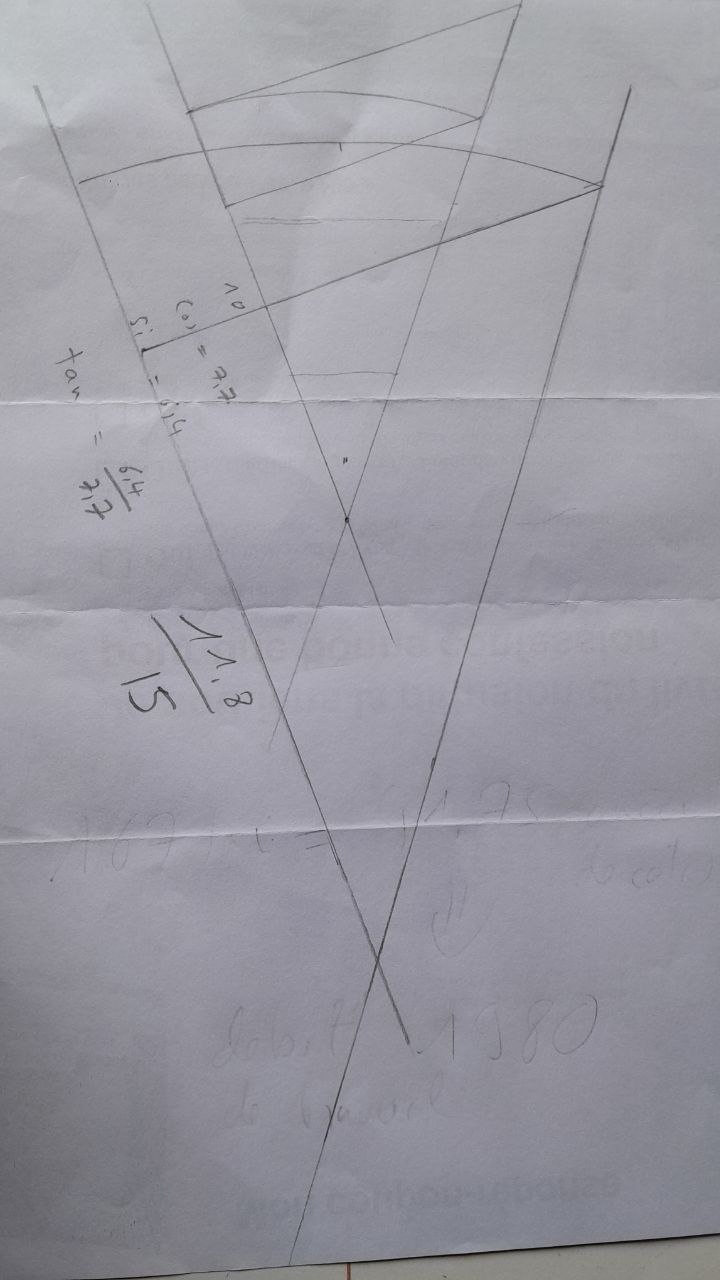
setprec=3
eingestellt sinM = 6.4;
eingestellt cosM = 7.7;
eingestellt sinM = 11.8;
eingestellt cosM = 15;
tanM einstellen = sinM/cosM;
tanM=0.787
#arctan(tanM) * 180 / pi =39.73 ô¯
arctan(tanM) * 180 / pi =38.191 ô¯
durchschnittlich :
19.86
19.09
=38.95
wenn man diesen Winkel durch zwei teilt, erhûÊlt man :
38.95 / 2 =19.475
(Berechnung mit dem algebraischen Rechner durchgefû¥hrt scalc )
der sich dem Winkel zwischen dem ûquator einer Kugel und den drei Berû¥hrungspunkten der Eckpunkte eines Tetraeders nûÊhert, das in diese Kugel einbeschrieben ist.
wobei der Pol die vierte Spitze des Tetraeders ist (vgl. ).
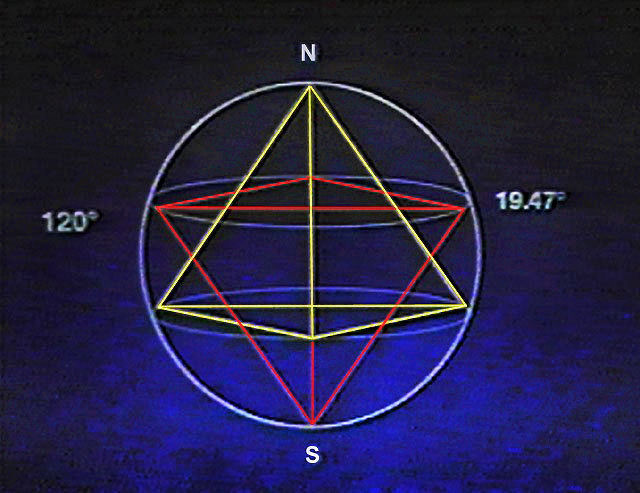
Es wû¥rde eine mathematische Studie erfordern, um die Existenz und den Wert dieses Winkels zu bestimmen.
2.Moebius Band Dreieck ausgewogen
wenn man aus einem Blatt Papier ein Moebiusband baut, indem man es so straff wie mûÑglich spannt,
Das heiût, Sie versuchen, die Schleife so eng wie mûÑglich zu machen.
applatisant die Struktur ist ein gleichseitiges Dreieck mit mehreren BlûÊttern.
Es gibt ein Mittelblatt, das von einer Seite auf die andere gekippt werden kann.
erinnert an den Schlag eines Herzens (Vorhof Ventrikel).
das menschliche Herz besteht aus zwei Herzen: eine fû¥r die arterielle Durchblutung,
und einen fû¥r den venûÑsen Kreislauf, wie im Bild oben mit den beiden ineinandergreifenden MûÑbiusringen mit unterschiedlicher HelizitûÊt dargestellt.
die Verschachtelung von zwei Tetraedern bildet den tetraedrischen_Stern.







